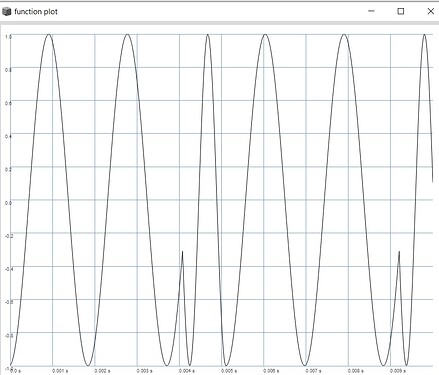
EDIT: The code now looks perfect on the plot for every vertical value.
But the transitions are really rough, there is a discontinuity for every integer value because of the case vertical == vertical.floor and its division trough zero. so ive implemented another Select.ar with BinaryOpUGen('==', vertical, vertical.floor. i think when this condition is met the signal should be rendered as a normal cosine, because no anti-aliasing is needed.
but this is probably wrong, because now the signal is not rendered as a smooth full-cycle sinusoid when the phase is inside an incomplete period any more. any ideas?
(
{
arg freq = 392;
var horizontal = \horizontal.kr(0.80);
var vertical = \vertical.kr(2.2);
var cos, phasor;
phasor = LFSaw.ar(freq/2,1).range(horizontal.neg, 1-horizontal);
phasor = phasor.bilin(0, horizontal.neg, 1-horizontal, vertical, 0, 1);
cos = Select.ar(phasor > vertical.floor,
[
(phasor * 2pi).cos.neg,
Select.ar(BinaryOpUGen('==', vertical, vertical.floor),
[
(phasor * 2pi).cos.neg,
((phasor.wrap(0,1)/(vertical-vertical.floor)*pi).cos*(vertical-vertical.floor)).neg-(vertical.ceil-vertical)
]
);
]
);
}.plot
)
EDIT: i tried the crossfade attempt once more because i couldnt figure out how to solve the case vertical = vertical.floor, the result is smooth for sweeping the vertical value but i dont know if its correct and it probably just fixes the vertical value, the aliasing is still prominent for extreme horizontal values.
(
~nearest_even = {|val|
var val_floor, val_ceil, res, distance;
val_floor = val.floor;
val_ceil = val.ceil;
res = Select.ar (val % 2,
[ val_floor, val_ceil ],
);
distance = (val - res).abs;
[res, distance];
};
~nearest_odd = {|val|
var val_floor, val_ceil, res, distance;
val_floor = val.floor;
val_ceil = val.ceil;
res = Select.ar (val + 1 % 2,
[ val_floor, val_ceil ],
);
distance = (val - res).abs;
[res, distance];
};
)
(
{
arg out=0, pan=0, amp=0.25, freq=110;
var horizontal = MouseX.kr(0.01,0.99);
var vertical = K2A.ar(MouseY.kr(1.0,10.0));
var vertical_even = ~nearest_even.(vertical);
var vertical_odd = ~nearest_odd.(vertical);
var cos, phasor, sig;
vertical = [vertical_even[0], vertical_odd[0]];
phasor = Phasor.ar(0, freq/2 * SampleDur.ir, horizontal.neg, 1-horizontal, horizontal.neg);
phasor = phasor.bilin(0, horizontal.neg, 1-horizontal, vertical, 0, 1);
cos = (phasor * 2pi).cos.neg;
sig = XFade2.ar(cos[0], cos[1], vertical_even[1] * 2 - 1);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig, pan, amp);
Out.ar(out, sig);
}.scope;
)
s.freqscope;
EDIT: the Phython Code from the Authors says something like this:
f0 = 500.
fs = 44100.
w0 = 2*pi*f0/fs
N = int(fs/f0)
t = arange(0,44100)
T = f0/fs
P = 1/T
d = 0.80
v = 2.20
# -- phase distortion function
def vps(x,d,v, suppress):
if x < d: p = (v*x)/d
else: p = (1-v)*(x-d)/(1-d) + v
# aliasing reduction
c1 = c2 = 0
if suppress:
if p > int(v):
c = v % 1
if 0 < c and c <= 0.5:
p = 0.5 * (p % 1) / c
c1 = 0.5 * (1 - cos(2*pi*c))
c2 = c1-1
else:
p = (p % 1) / c
if p > 0.5:
c1 = 0.5 * (1 + cos(2*pi*c))
c2 = 1-c1
return p,c1,c2
# -- signal generation
def process(d,v, suppress):
y = zeros(len(t))
x = zeros(len(t))
phi = 0
for n in range(0,len(t)):
p,c1,c2 = vps(phi,d,v, suppress)
y[n] = -cos(2*pi*p) # waveshaping
x[n] = p
if c1 != 0:
y[n] = y[n]*c1 + c2
phi += T
if phi > 1: phi -= 1
return y,x
# -- spectrum
def spectrum(s):
NFFT = 16384*2
NFFT2 = 16384
NWIN = 16384
win = chebwin(NWIN, 120)
win = append(win, zeros(NFFT-NWIN))
scal = NFFT*sqrt(mean(win**2))
spec = fft(win*s[0:NFFT])
mags = sqrt(spec[0:NFFT2].real**2 + spec[0:NFFT2].imag**2)
norm = 20*log10(mags/scal)
spec = norm - max(norm)
return spec
# -- main
y1,x1 = process(d,v, False)
y2,x2 = process(d,v, True)