Pwalk: how do you always fold at both boundaries?

[PitchTrebler]

Hello everyone,

I’m trying to find a pattern that will do a random walk over a list, and when it reaches a boundary, it always folds back towards the center. I expected Pwalk could easily achieve this behavior, but I can’t figure out how to do it.

The help file for Pwalk says to use directionPattern = 1 to wrap, so I would expect -1 to fold, but I get unexpected results with the most simple use cases. Here I try both directions, and neither one works as expected on both boundaries:

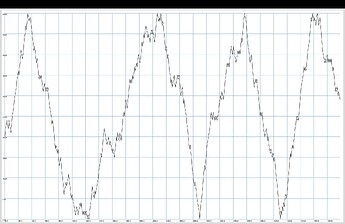
Pwalk([5.1, 6, 7], Prand([-1, 1], 30), -1).iter.all;
// ...folds at upper bound, but wraps at lower bound

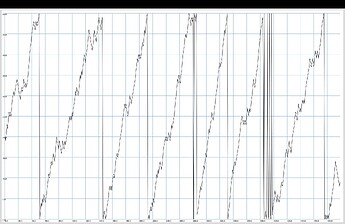
Pwalk([5.1, 6, 7], Prand([-1, 1], 30), 1).iter.all;
// ...folds at lower bound, but wraps at upper bound

It seems that Pwalk needs to treat each boundary differently in order to achieve my desired result, but after looking at the source code, I don’t think Pwalk can do this. Please correct me if I’m wrong.

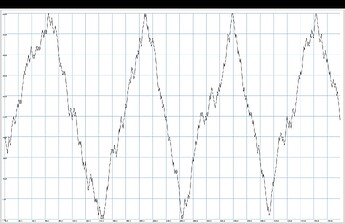
I have come up with this workaround using Pbrown, but it has its own limitations:

Pbrown(0, 2, 1).collect([5.1, 6, 7].at(_)).iter.nextN(20);

That works fine for this simple case, but Pbrown is limited in that it can’t do more complicated (i.e. asymmetrical) step patterns, and you can’t embed Pbinds in the resulting stream, as far as I can tell.

So my question is, is it possible to achieve this folded random walk pattern with Pwalk, and if so, what is the directionPattern that does this? Or is there some other pattern class that I should be using? I know I could use Prout and write all the logic myself, but if that’s the case I’d prefer to write a new pattern class.

[jamshark70]

@PitchTrebler

It seems that Pwalk needs to treat each boundary differently in order to achieve my desired result, but after looking at the source code, I don’t think Pwalk can do this.

No, there’s an example in the help, “non-random walk: easy way to do up-and-down arpeggiation.”

Set directionPattern to Pseq([1, -1], inf).

hjh

[PitchTrebler]

That works for non-random stepPatterns, but it doesn’t produce folding behavior for random stepPatterns. The following line of code with random stepPattern does not always fold (you might have to run a few times to see it wrap):

Pwalk([0, 1, 2], Prand([-1, 1], 10), Pseq([1, -1], inf)).iter.all;
// -> [ 0, 2, 0, 1, 2, 1, 0, 1, 0, 2 ]

Is there a way to guarantee that it always folds, regardless of the stepPattern input?

EDIT: Actually, directionPattern: Pseq([1, -1], inf) is not even guaranteed to fold non-random stepPatterns. Consider this pattern:

Pwalk([0, 1, 2], Pseq([1, -1, -1], 3), Pseq([1, -1], inf)).iter.all;
// -> [ 0, 1, 0, 2, 1, 2, 0, 1, 0 ]

[PitchTrebler]

I made a subclass of Pwalk to implement this behavior. It’s like Pwalk, but with an additional argument boundaryBehavior to choose the desired behavior at each boundary.

boundaryBehavior can be a symbol (\fold, \clip, \wrap) or a custom function, or a pattern/stream that yields those things. It can also be an array of 2 items, like [\fold, \clip] to get different behaviors at the lower and upper bounds, respectively.

Here’s the source code. I haven’t tested it much, so let me know if you find any bugs or other ways to improve it…

// Pwalk2.sc
// save this in Platform.userExtensionDir
// then...
// thisProcess.recompile;

Pwalk2 : Pwalk {
    var <>boundaryBehavior;

    *new { arg list, stepPattern, directionPattern = 1, startPos = 0, boundaryBehavior = \fold;
        ^super.new(list, stepPattern, directionPattern, startPos)
        .boundaryBehavior_(boundaryBehavior);
	}

	storeArgs { ^[list, stepPattern, directionPattern, startPos, boundaryBehavior] }

    embedInStream { arg inval;
		var	step;
		var index = startPos.value(inval);
		var stepStream = stepPattern.asStream;
		var directionStream = directionPattern.asStream;
		var direction = directionStream.next(inval) ? 1;
        var behaviorStream = boundaryBehavior.asStream;
        direction = direction.asArray.at(0);

		while({
			(step = stepStream.next(inval)).notNil
		},{
			inval = list[index].embedInStream(inval);
            step = step * direction.value(inval);
            index = index + step;
            if(index < 0 or: {index >= list.size}) {
                var whichBoundary = (index > 0).asInteger;
                var behavior = behaviorStream.next(inval).asArray;
                behavior = behavior.wrapAt(whichBoundary);
                direction = directionStream.next(inval) ? 1;
                direction = direction.asArray.wrapAt(whichBoundary);
                if(behavior.isFunction) {
                    index = behavior.(index, 0, list.size - 1);
                } {
                    index = index.perform(behavior, 0, list.size - 1);
                };
                index = index.fold(0, list.size - 1);
            }
		});

		^inval;
	}
}

And some examples…

// fold and reverse direction at boundaries:
Pwalk2((0..50), Prand([-1, 1, 2], inf), Pseq([1, -1], inf), 20, \fold).iter.nextN(500).plot;

// wrap:
Pwalk2((0..50), Prand([-1, 1, 2], inf), 1, 20, \wrap).iter.nextN(500).plot;

// array of 2 behaviors: fold at lower bound, clip at upper bound:
Pwalk2((0..50), Prand([-1, 1, 2], inf), Pseq([1, -1], inf), 20, [\fold, \clip]).iter.nextN(500).plot;

// array of 2 behavior functions:
(
Pwalk2((0..50), Prand([-1, 1, 2], inf), Pseq([1, -1], inf), 20,
    [
        {|idx, lo, hi| rrand(lo, hi)}, // choose random index at lower bound
        {|idx| idx.div(2)} // divide by 2 at upper bound
    ]
).iter.nextN(500).plot;
)

[smoge]

very cool!

The first thing I assumed about it was that the direction was some probabilistic procedure with a strong tendency to one direction.

Something like:

var dirProb = directionStream.next(inval) ? 1;
dirProb = dirProb.abs.clip(0.0, 1.0);
direction = if(dirProb.coin) { 1 } { -1 };

There is a possibility of more or less subtle biases and more unexpected movements.

Or did I miss the entire point of the Pattern???

Some quick hacks based on your code (just for fun and show the idea)

Pwalk2 : Pwalk {
    var <>boundaryBehavior;
    
    *new { arg list, stepPattern, directionPattern = 1, startPos = 0, boundaryBehavior = \fold;
        ^super.new(list, stepPattern, directionPattern, startPos)
        .boundaryBehavior_(boundaryBehavior)
    }
    
    storeArgs { 
        ^[list, stepPattern, directionPattern, startPos, boundaryBehavior] 
    }
    
    embedInStream { arg inval;
        var step;
        var index = startPos.value(inval);
        var stepStream = stepPattern.asStream;
        var directionStream = directionPattern.asStream;
        var behaviorStream = boundaryBehavior.asStream;
        var direction;
        
        while({
            (step = stepStream.next(inval)).notNil
        }, {
            inval = list[index].embedInStream(inval);
            
            var dirProb = directionStream.next(inval) ? 1;
            dirProb = dirProb.abs.clip(0.0, 1.0); 
            
            direction = if(dirProb.coin) { 1 } { -1 };
            
            step = step * direction;
            index = index + step;
            
            
            if(index < 0 or: {index >= list.size}) {
                var whichBoundary = (index > 0).asInteger;
                var behavior = behaviorStream.next(inval).asArray;
                behavior = behavior.wrapAt(whichBoundary);
                
                if(behavior.isFunction) {
                    index = behavior.(index, 0, list.size - 1);
                } {
                    index = index.perform(behavior, 0, list.size - 1);
                };
                index = index.fold(0, list.size - 1);
            };
        });
        ^inval;
    }
}

EDIT: downsides: no guarantee of direction changes, boundary behavior is less distinct and takes more time

[jamshark70]

@PitchTrebler

That works for non-random stepPatterns, but it doesn’t produce folding behavior for random stepPatterns.

Ah, sorry, I forgot to come back to this.

I’m not sure a whole new class is needed… if this does the job for you, it’s less code = easier maintenance.

(
~foldWalk = { |list, stepPattern|
	Pindex(
		list,
		Pseries(
			list.size.rand,
			stepPattern,
			inf
		).fold(0, list.size-1),
		inf
	)
};
)

~foldWalk.((0..100), Prand((-10 .. 10).reject(_ == 0), inf))
.asStream.nextN(1024)
.plot;

@smoge

The first thing I assumed about it was that the direction was some probabilistic procedure with a strong tendency to one direction.

I’m pretty sure that’s what I was thinking when I wrote Pwalk – but I forget now.

hjh

[PitchTrebler]

@jamshark70

I’m not sure a whole new class is needed… if this does the job for you, it’s less code = easier maintenance.

Thanks James, that does the job It didn’t occur to me to use Pseries in that way, but it solves my original question quite elegantly. I will probably still use the new class in my own code, just because it provides a convenient way to choose different boundary behaviors.

@smoge

Something like:

var dirProb = directionStream.next(inval) ? 1;
dirProb = dirProb.abs.clip(0.0, 1.0);
direction = if(dirProb.coin) { 1 } { -1 };

Good idea! Although it’s already possible to treat directionPattern like a probability. It just requires a little extra code when writing the pattern:

Pwalk((0..2), Prand([-1, 1], 20), Pwrand([1, -1], Pwhite(0.0, 1).collect{|p| [p, 1 - p]}, inf)).iter.all;
Pwalk2((0..2), Prand([-1, 1], 20), {var prob = 1.0.rand; [1, -1].wchoose([prob, 1 - prob])}).iter.all;

I should mention that in Pwalk2 the directionPattern can also accept different magnitudes (other than 1), so there is some flexibility there, e.g.

( // speed up every time you hit a boundary:
Pwalk2(
    (0..50),
    Prand([-1, 1, 2], inf),
    Pseq([1, -1], inf) * Pseries(1, 0.15),
    20,
    \fold
).iter.nextN(500).plot;
)

[smoge]

@PitchTrebler

It didn’t occur to me to use Pseries in that way,

In fact, Pseries is the walk itself, which can also become a random walk (like Pwalk) with the correct parameters.

We just needed walk (Pseries in sc3) to build all kinds of walks, like random walks, and this one.

[jamshark70]

There is actually one problem with Pseries().fold though:

Pseries(1, 2, inf).fold(0, 10).asStream.nextN(10)
-> [ 1, 3, 5, 7, 9, 9, 7, 5, 3, 1 ]

9 goes up by 2, and folds back to… 9.

I think this is why Pwalk is written the way it is:

Pwalk((0..10), 2, Pseq([1, -1], inf), startPos: 1).asStream.nextN(10)

-> [ 1, 3, 5, 7, 9, 7, 5, 3, 1, 3 ]

… where the Pwalk logic at 9 is: “9+2 would cross the upper boundary, so pull the next value from the directionStream, and then apply that to the step size 2 – then 9 + (2 * -1) → 7.”

And now I see what is the bug in Pwalk – it corrupts the step before checking the boundary, so then the attempt to recover may double-invert the step direction and cross the boundary anyway.

This version of embedInStream fixes the problem, by not overwriting step as step * direction:

	embedInStream { arg inval;
		var	step, stepDir;
		var index = startPos.value(inval);
		var stepStream = stepPattern.asStream;
		var directionStream = directionPattern.asStream;
		// 1 = use steps as is; -1 = reverse direction
		var direction = directionStream.next(inval) ? 1;		// start with first value

		while({
			// get step, stop when nil
			(step = stepStream.next(inval)).notNil
		},{
			inval = list[index].embedInStream(inval);  // get value/stream out
			stepDir = step * direction;	// apply direction
				// if next thing will be out of bounds
			if(((index + stepDir) < 0) or: { (index + stepDir) >= list.size }, {
				direction = directionStream.next(inval) ? 1;  // next direction, or 1
				stepDir = step * direction;  // apply to this step
			});
			index = (index + stepDir) % list.size;
		});

		^inval;
	}

hjh