hey,
the desired output of your grain scheduling phasor are linear ramps between 0 and 1. Therefore you cannot modulate the frequency of your grain scheduling phasor without implementing a sample and hold triggered by a trigger derived from the grain scheduling phasor itself inside a single-sample feedback loop.
This would look like this in gen~:
Thats the reason for the randomPeriods function. Its output are always linear ramps between 0 and 1. The implementation of 2 ** (bipolar signal * modDepth) is the formula beeing used for exponential FM, for modDepths of 0 it collapses neatly to 1 and therefore outputs the linear ramps unchanged. The limit of the modDepth (randomness param) isnt 1, you can set it even higher and the ramps will still be linear and between 0 and 1.
(
var randomPeriods = { |rate, randomness|
var events = 2 ** (Dwhite(-1, 1) * randomness) / rate;
var duration = Ddup(2, events);
Duty.ar(duration, DC.ar(0), 1 / duration);
};
{
var rate = \rate.kr(100);
var seq = randomPeriods.(rate, \randomness.kr(2));
Phasor.ar(DC.ar(0), seq * SampleDur.ir);
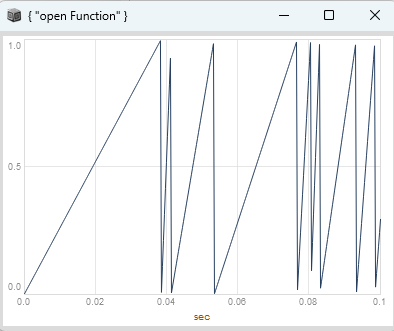
}.plot(0.1);
)
The only issue, and we have discussed this before, is the round-robin method combined with random durations and overlap.
If you set the randomness param to “higher values” and additionally raise the overlap param to its maximum value, determined by the number of channels you use, you can see that some of the phases wont reach 1.
The windows beeing driven by that phase wont reach their end but will abruptly end in the middle of their duration. This is undesirable but unanvoidable with the combination of these two techniques.
The phases are still linear thats good, but for extreme settings wont reach 1. Thats still better then additionally having non-linear phases from modulation without the implementation of a sample and hold in the single sample feedback loop.