SynthDef optimization strategies (esp wrt non-sclang clients)

[TimWalters]

That makes sense. Thanks a lot for elaborating on this!

@jordan

You could do less by applying fewer optimisations.

My own 100% personal take is this: over almost thirty years of using SuperCollider, I don’t remember any server usage surprises that didn’t turn out to be due to my mistake. Whereas I have torn my hair out many times trying to figure out what was going wrong only to eventually find out (usually by trawling through the source code) that sclang was doing something “helpful” that was breaking my code. The vast majority of these were in the Pattern library, which is full of black magic, rather than building SynthDefs, but still–I am leery of code that does things behind my back. Admittedly, the difference between “behind my back” and “sensible default” can be hard to define.

This could all be down to my musical style not requiring certain kinds of defs–it’s certainly not my mad coding skillz–but I really think there is something to be said for SynthDef code that mirrors what’s actually happening on the server. It might be a little harder for beginners, but if optimization keeps fixing beginner mistakes, then people tend to stay beginners for longer.

I would still be very interested in seeing an example of poor optimization that can’t be fixed by correctly writing the def.

[Spacechild1]

@TimWalters

I would still be very interested in seeing an example of poor optimization that can’t be fixed by correctly writing the def.

The problem is that optimal SynthDef code isn’t always the most idiomatic one. One prominent example would be multichannel-expansion; it is very idiomatic, but leads to terrible Ugen ordering by default and thus has to be fixed with the additional topological (depth-first) sort.

[jordan]

@TimWalters

rather than building SynthDefs

Just to give an example of where synthdef gets it wrong and why it’s not a good idea to emulated it’s output when designing one.

Here’s an example

var sig0 = In.ar(\a.kr);
var sig1 = In.ar(\b.kr);
var rd = PlayBuf.ar(1);
var wr = RecordBuf.ar(1);
Out.ar(\c.kr, sig0);
Out.ar(\d.kr, sig1);

Here’s the order.

[0_In, audio, \a.kr]]
[1_Out, audio, \c.kr, 0_In]
[2_In, audio, \b.kr]
[3_Out, audio, \d.kr, 2_In]
[4_PlayBuf, audio, [0, 1.0, 1.0, 0.0, 0.0, 0]]
[5_RecordBuf, audio, [0, 0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0, 1]]

Even in this simple example, the ordering of the ins and out is wrong… but… you will only hear this if \a == \c == \b, which is unusual, meaning you don’t often run into this, but it is still an important mistake in the compiler. This is more common when working with buffers where this type of thing actually makes sense.

The correct ordering is to move the buffer ugens to the top or bottom, but to keep the ins above the outs, although the order of the ins or outs doesn’t actually matter.

@TimWalters

if optimization keeps fixing beginner mistakes, then people tend to stay beginners for longer.

In this particular case, I don’t see why knowledge of how to eek the most out of the server is valuable.

[TimWalters]

I get

[ 0_Control, control, nil ]
[ 1_In, audio, [ 0_Control[0] ] ]
[ 2_Control, control, nil ]
[ 3_In, audio, [ 2_Control[0] ] ]
[ 4_PlayBuf, audio, [ 0, 1.0, 1.0, 0.0, 0.0, 0 ] ]
[ 5_RecordBuf, audio, [ 0, 0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0, 1 ] ]
[ 6_Control, control, nil ]
[ 7_Out, audio, [ 6_Control[0], 1_In[0] ] ]
[ 8_Control, control, nil ]
[ 9_Out, audio, [ 8_Control[0], 3_In[0] ] ]

which seems OK? My still-naive parser would put all the controls at the top, but otherwise be the same.

@jordan

The correct ordering is to move the buffer ugens to the top or bottom

Why is that important?

In general, other than “cause should precede effect,” what are the standards for “correct” order? Are they documented somewhere?

[jordan]

Ah I added the controls in later for clarity, when I ran it with hard coded numbers I got that ordering.
Here is better example:

SynthDef(\a, {
	var sig0 = In.ar(0);
	var sig1 = In.ar(0); // sig1 != sig0, but 2 * sig0
	Out.ar(0, sig0);
	Out.ar(0, sig1);
}).dumpUGens

[0_In, audio, [0]]
[1_Out, audio, [0, 0_In[0]]]
[2_In, audio, [0]]
[3_Out, audio, [0, 2_In[0]]]

My version produces this

[0_In, audio, [0], [], [2_Out, 1_Out], [], [2_Out, 1_Out]]
[1_Out, audio, [0, 0_In[0]], [0_In[0]], [], [0_In], []]
[2_Out, audio, [0, 0_In[0]], [0_In], [], [0_In], []]

The buffer read should go in a separate block as it doesn’t effect the inputs and outputs and will reduce wirebufs, controls should be interleaved with other ugens for the same reason.

What are the standards for “correct” order? Are they documented somewhere?

Not documented, the approach I’ve taken is to define a was of disabling optimisations and checking they pass a null test within some threshold. This way, any reordering and rewriting is permissible, so long as it sounds the same.

[jamshark70]

Since it came up a couple of times (the idea that it’s better for users to write pre-optimized code): One case where I very much appreciate CSE optimization is repeated calls to linlin, linexp or lincurve.

(
SynthDef(\redundancy, { |out, outLow = 1, outHigh = 10|
	var lfos = NamedControl.kr(\lfos, Array.fill(10, 0));
	Out.kr(out, lfos.linlin(-1, 1, outLow, outHigh));
}).add.dumpUGens;
)

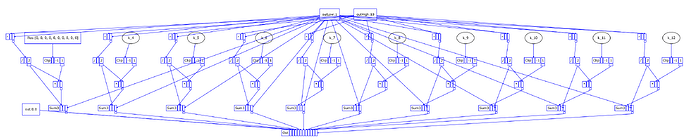
Current dev:

[0_Control, control, nil]
[1_-, control, [0_Control[2], 0_Control[1]]]
[2_/, control, [1_-, 2]]
[3_-, control, [0_Control[2], 0_Control[1]]]
[4_/, control, [3_-, 2]]

... repeated exactly(!) for 10 channels

[21_Control, control, nil]
[22_Clip, control, [21_Control[0], -1, 1]]
[23_*, control, [22_Clip, 2_/]]
[24_Sum3, control, [23_*, 2_/, 0_Control[1]]]
[25_Clip, control, [21_Control[1], -1, 1]]
[26_*, control, [25_Clip, 4_/]]
[27_Sum3, control, [26_*, 4_/, 0_Control[1]]]

... these cannot be optimized out: 10 channels, OK

[52_Out, control, [0_Control[0], 24_Sum3, 27_Sum3, 30_Sum3, 33_Sum3, 36_Sum3, 39_Sum3, 42_Sum3, 45_Sum3, 48_Sum3, 51_Sum3]]

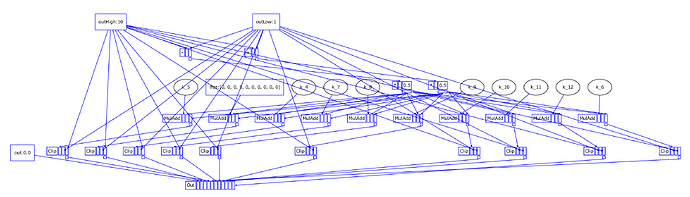
Using my UGenCache (private extension):

[0_Control, control, nil]
[1_-, control, [0_Control[2], 0_Control[1]]]
[2_/, control, [1_-, 2]]
[3_neg, control, [2_/]]
[4_-, control, [0_Control[1], 3_neg]]
[5_Control, control, nil]
[6_Clip, control, [5_Control[0], -1, 1]]
[7_MulAdd, control, [6_Clip, 2_/, 4_-]]
[8_Clip, control, [5_Control[1], -1, 1]]
[9_MulAdd, control, [8_Clip, 2_/, 4_-]]

(required channel calculations...)

[26_Out, control, [0_Control[0], 7_MulAdd, 9_MulAdd, 11_MulAdd, 13_MulAdd, 15_MulAdd, 17_MulAdd, 19_MulAdd, 21_MulAdd, 23_MulAdd, 25_MulAdd]]

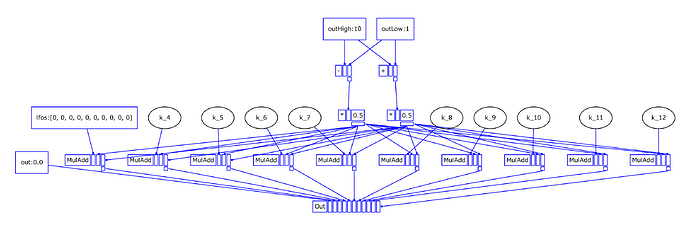
Using Jordan’s dup-smasher (which curiously ends up with 3 units per channel, rather than the 2 that mine manages – I think this is because my approach never enters the duplicate math operations into the graph at all – if instead you have the graph with redundancies, then apply Sum3 optimization, then remove duplicate units, this specific case ends up being less efficient – this underscores a point Scott Wilson raised a little while ago, that it’s extremely difficult to come up with an optimization strategy that handles every case optimally):

[0_Control, control, [0.0, 1, 10]]
[1_-, control, [0_Control[2], 0_Control[1]]]
[2_/, control, [1_-, 2]]
[3_Control, control, [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
[4_Clip, control, [3_Control[0], -1, 1]]
[5_*, control, [4_Clip, 2_/]]
[6_Sum3, control, [5_*, 0_Control[1], 2_/]]
[7_Clip, control, [3_Control[1], -1, 1]]
[8_*, control, [7_Clip, 2_/]]
[9_Sum3, control, [8_*, 0_Control[1], 2_/]]

... channels...

[34_Out, control, [0_Control[0], 6_Sum3, 9_Sum3, 12_Sum3, 15_Sum3, 18_Sum3, 21_Sum3, 24_Sum3, 27_Sum3, 30_Sum3, 33_Sum3]]

To hand-optimize it, you have to do this. (The lincurve formula is quite a bit more complex = inconvenience for looking up the formula, and more chances to make mistakes.)

(
SynthDef(\subexpression, { |out, outLow = 1, outHigh = 10|
	var lfos = NamedControl.kr(\lfos, Array.fill(10, 0));
	var scale = (outHigh - outLow) / 2;
	var offset = 1 - (scale * -1);
	Out.kr(out, lfos.clip(-1, 1) * scale + offset);
}).add.dumpUGens;
)

… or, SC could implement linlin/linexp/lincurve for arrays, and pre-optimize there. At least, I think here, the user shouldn’t be burdened with this.

Another case would be multiChannel.collect { |chan| chan = BLowPass4.ar(chan, ...); chan = AnotherOp.ar(...); chan }.

FWIW, the existence of optimizations doesn’t prevent the user from hand-optimizing (which I still do, in some places – the fact that I experimented with a UGenCache for limited CSE doesn’t mean that I now deliberately write redundant subexpressions).

hjh

[smoge]

@TimWalters

Maybe I’m misunderstanding what you mean by subexpression. If you mean something like:

osc1 = SinOsc(110) * SinOsc(5 * 3)
osc2 = SinOsc(55 * 2) * SinOsc(15)

then elimination of osc2 would happen automatically by removing duplicate nodes, either before or after building the subtrees. Both osc1 and osc2 would point to the same instance of Mul(SinOsc(110), SinOsc(15)). There’s no need to handle subexpressions separately.

Yes, that’s the case when it is reduced to a constant. However, there are cases where subexpressions involve UGens, which are not all equal. The example in the hsc3 helps explain the difference between a SinOsc and a WhiteNoise. Noise Ugens, in this case, are monadic (m Ugen), since reducing Noise Ugens as a SinOsc (i.e. mixing expressions and computations) would radically change the graph into something wholly different and incorrect. It is an elegant approach since it is not an ad hoc fix but expresses the (computation/spaces/logic) correspondence of various processes as types (aka Curry–Howard for some, aka “overengineering” for others ).

In that sense, I wondered if Lua would give something like that for free, or (I believe) you would need to write/design it.

Haskell sort of directs the implementation this way. hsc3 makes that clear; the user is aware of this, which might be good or bad, depending on your design goals.

Edit: (Another thing I noticed in hsc3 is the lack of the topo sort optimization, which (I think) it’s possible is not necessary for a lazy-evaluated referential-transparent language since the language itself is evaluated as an optimized graph anyway. In other words, the evaluation order is already determined by data dependencies everywhere, which can result in an optimized evaluation graph without explicit topological sorting. It would be nice to confirm this.)

Edit: (I think the recent proposal basically tries to be more referentially transparent re: UGens in its own way.)

[TimWalters]

OK, but it’s worth noting that this is also an example of my complaints about sclang giving unexpected results. If you expand .linlin to what one would expect it to be doing:

(
SynthDef(\redundancy, { |out, outLow = 1, outHigh = 10|
	var lfos = NamedControl.kr(\lfos, Array.fill(10, 0));
	Out.kr(out, lfos.collect { |l| LinLin.kr(l, -1, 1, outLow, outHigh) });
}).add.dumpUGens;
)

you already get a better naive result:

[ 0_Control, control, nil ]
...
[ 42_Out, control, [ 0_Control[0], 23_Sum3, 25_Sum3, 27_Sum3, 29_Sum3, 31_Sum3, 33_Sum3, 35_Sum3, 37_Sum3, 39_Sum3, 41_Sum3 ] ]

That said, you’re right, this is an example where optimization can do something the user shouldn’t be expected to.

[TimWalters]

I see what you’re saying now. No, Lua certainly has no concept of monads!

[smoge]

(I imagine you know all this, but just for completeness)

Well, we don’t need to buy the whole package. We may want to capture the main idea that WhiteNoise should be treated differently from deterministic UGens. In this case, each “instance” of WhiteNoise should be unique, even if created with the same parameters. CSE and optimizations will work better and correctly if that difference is transparent. SinOsc is deterministic and can be safely treated as an expression, and many optimizations in SCLang traditionally try to target only PureUgens for this very reason.

Your example (that Lua would simplify the expressions)

osc1 = SinOsc(110) * SinOsc(5 * 3)
osc2 = SinOsc(55 * 2) * SinOsc(15)

would be incorrect if Lua makes the same here:

sound1 = WhiteNoise(0.2) * SinOsc(0.1)
sound2 = WhiteNoise(0.2) * SinOsc(0.1)

In both cases, SinOsc can be treated as an expression just as safely as a constant. On the other hand, the second optimization here should preserve both noise instances as unique and may use one SinOsc or do nothing.

[jamshark70]

@TimWalters

OK, but it’s worth noting that this is also an example of my complaints about sclang giving unexpected results. If you expand .linlin to what one would expect it to be doing … you already get a better naive result:

The “gain” here is because LinLin.kr omits the clipping stage (hence not an optimization).

LinLin.kr(in, srclo, srchi, dstlo, dsthi)
x.linlin(inMin, inMax, outMin, outMax, clip)  // default clip is \minmax

If you expand it literally to this:

(
SynthDef(\redundancy, { |out, outLow = 1, outHigh = 10|
	var lfos = NamedControl.kr(\lfos, Array.fill(10, 0));
	Out.kr(out, lfos.collect { |l| l.linlin(-1, 1, outLow, outHigh) });
}).add.dumpUGens;
)

… then it’s exactly the same. FWIW I would expect an n-ary math operator to multichannel expand to eachChannel.operator(args) and not magically switch to a pseudo-UGen (since not every n-ary op has a direct UGen equivalent). (One could argue that the clipping should go into LinLin… yeah, OK… but I don’t think the clipping itself is an unexpected result.)

hjh

[smoge]

A simple manual rewrite is to calculate scale and offset once (UGens 1-4) instead of 10 times (UGens 1-20). Also, use MulAdd instead of multiplication and Sum3 UGens (each channel). Thus, 53 Ugens are reduced to 26. That’s just simple expression simplification (both using “clip” ).

 (
SynthDef(\redudancy, { |out, outLow = 1, outHigh = 10|
    var lfos = NamedControl.kr(\lfos, Array.fill(10, 0));
    var scale = (outHigh - outLow) * 0.5;
    var midpoint = (outHigh + outLow) * 0.5;
    Out.kr(out, (lfos * scale + midpoint).clip(outLow, outHigh));
}).add.dumpUGens;
)

If the input is safe to be in range (which makes sense do to), then from 53 to 16 UGens (can be written with LinLin.kr)

    var lfos = \lfos.kr(Array.fill(10, 0));
    var mapped = lfos * ((outHigh - outLow) * 0.5) + ((outHigh + outLow) * 0.5); 

This version is much more idiomatic and also uses 16 UGens: everything without sacrificing anything ?

(
SynthDef(\redudancy, { |out, outLow = 1, outHigh = 10|
    var lfos = \lfos.kr(Array.fill(10, 0), spec: \bipolar.asSpec);
    var mapped = LinLin.kr(lfos, -1, 1, outLow, outHigh); 
    Out.kr(out, mapped);
}).draw
)


[0_Control, control, nil]
[1_-, control, [0_Control[2], 0_Control[1]]]
[2_*, control, [1_-, 0.5]]
[3_+, control, [0_Control[2], 0_Control[1]]]
[4_*, control, [3_+, 0.5]]
[5_Control, control, nil]
[6_MulAdd, control, [5_Control[0], 2_*, 4_*]]
[7_MulAdd, control, [5_Control[1], 2_*, 4_*]]
[8_MulAdd, control, [5_Control[2], 2_*, 4_*]]
[9_MulAdd, control, [5_Control[3], 2_*, 4_*]]
[10_MulAdd, control, [5_Control[4], 2_*, 4_*]]
[11_MulAdd, control, [5_Control[5], 2_*, 4_*]]
[12_MulAdd, control, [5_Control[6], 2_*, 4_*]]
[13_MulAdd, control, [5_Control[7], 2_*, 4_*]]
[14_MulAdd, control, [5_Control[8], 2_*, 4_*]]
[15_MulAdd, control, [5_Control[9], 2_*, 4_*]]
[16_Out, control, [0_Control[0], 6_MulAdd, 7_MulAdd, 8_MulAdd, 9_MulAdd, 10_MulAdd, 11_MulAdd, 12_MulAdd, 13_MulAdd, 14_MulAdd, 15_MulAdd]]

[jordan]

I think your diagnosis of my version not optimising enough isn’t quite correct, because my version does produce the minimal when you try turn it to audio rate … Hm!! Something is clearly broken…

[jamshark70]

@smoge

A simple manual rewrite is to calculate scale and offset once (UGens 1-4) instead of 10 times (UGens 1-20).

A similar version is included in my post

A manual rewrite of a .collect { |channel| BLowPass4.ar(channel, ...) } would require the user to replicate the biquad transform. In this case, standard multichannel expansion sidesteps the issue (coefficients are then calculated once for all channels), so the issue doesn’t arise in a common scenario. But there may be cases where the BLowPass4 is lumped in with other operations – particularly if each channel needs to be paired up with a channel from a different multichannel signal, in a way which normal MCE doesn’t handle, then the .collect may be unavoidable. Even Pd doesn’t have cases where users would need to roll their own biquad for optimal performance

hjh

[TimWalters]

@jamshark70

but I don’t think the clipping itself is an unexpected result

It’s completely unexpected to me! I still remember discovering that the reason my code wasn’t working was that I was trying to define a per-octave response by something like .linlin(0, 12, x, y).midicps. Yes, it’s documented (although my experience was long enough ago that I’m not sure it was then), but there’s no reason a priori to expect a slope-changer to clip.

Oh well, TIL that there’s an argument to turn it off (so that I don’t have to calculate my endpoints by hand anymore) and that the UGen version doesn’t do it.

[jordan]

@jamshark70

Using Jordan’s dup-smasher (which curiously ends up with 3 units per channel, rather than the 2 that mine manages – I think this is because my approach never enters the duplicate math operations into the graph at all – if instead you have the graph with redundancies, then apply Sum3 optimization, then remove duplicate units, this specific case ends up being less efficient – this underscores a point Scott Wilson raised a little while ago, that it’s extremely difficult to come up with an optimization strategy that handles every case optimally)

So I figured this out.

My one applies optimisations from the bottom of the graph (output) to the top (input), but when it does an optimisation, it steps back down the graph to re-run the optimiser on the new UGens.

The existing only walks down the graph following the ordering they were created in, and never reruns on the newly created UGens, meaning the result is determined by the input order.

There will always be issues where they don’t quite meet up, however I have fixed this particular issue by making the BinaryOpUGen(*) check its descendants to see if there is (not just a BinaryOpUGen(+)), but also Sum3 and Sum4, which it only rewrites if there is more than one descendent.

Also, .linlin returns a MulAdd in audio rate, but not control rate.