8-bit Shift register

[dietcv]

hey, in the book “generating sound & organising time - thinking with ~gen” is an example how to implement a basic 8-bit shift register in ~gen and some further examples how to implement binary decoding and some further extensions like limiting, extraction, rotation. inversion etc… One oberservation from the book is that binary encoding encodes a unique integer for every different possible sequence of bits, and vice versa: every integer encodes a unique gate pattern, so that the entire pattern can be represented as a single integer at any time.

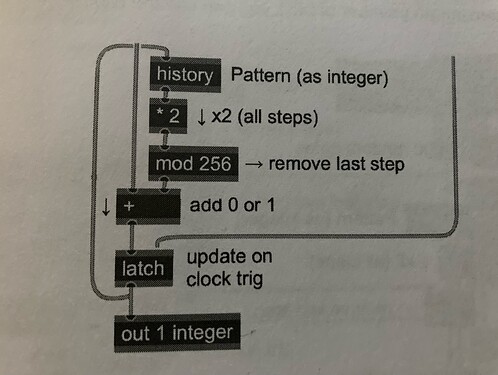
So the same results could be produced just by a few operations on integer signals rather then shuffling gates through a series of shift registers. It is stated that every clock step shifts each gate one step to the right, which effectively doubles its contribution to the output. That would be equivalent to multiplying the whole integers by two. The first step input then adds a new gate either 0 or 1 to the sum. To keep the range of 0 to 255 a modulo operator is used.

For each clock trigger, the currently stored integer (equivalent to shifting the entire binary pattern right by 1 step) is doubled; and a new input (which is either 0 or 1) is added, and then any additional bits beyond stage 8 are removed by using a modulo operator.

Could someone help me out to implement the basic single sample feedback loop with Demand Ugens (Dbufrd and Dbufwr) to create it in SC? Im not sure how the Latch Ugen could be implemented in the single sample feedback path in SC. After that a Xor gate is added for a LFSR and some interesting other techniques to work with the bits of an integer. But thats the basic patch in ~gen:

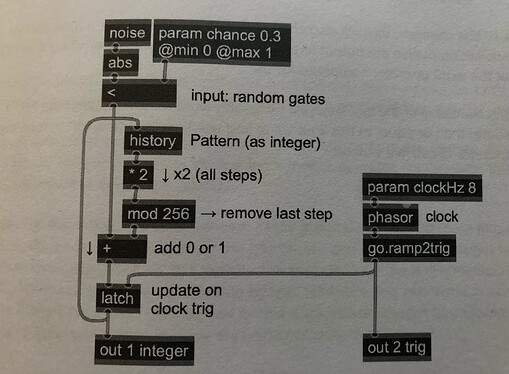
with input source and clock added:

[TXMod]

I’m not sure if this is helpful but DNoiseRing is a UGen in SC3 Plugins that is a Demand rate shift register generator:
https://doc.sccode.org/Classes/DNoiseRing.html
and is an implementation of this:

Wiard NoiseRing

Best,
Paul

[dietcv]

hey, thanks for your reply. i know this Ugen. I think the purpose of the post is to figure out how SC can do things which are available in ~gen which i would consider as the state of the art approchable way to implement sample by sample synthesis procedures by users which have a basic amount of programming knowledge. Long term short i dont want an arbitrary shift register, i want exactly the one implemented in ~gen from the book and want understand how that works based on current literature and move from there. If thats possible feel free to let me know.

[jamshark70]

@dietcv

Long term short i dont want an arbitrary shift register, i want exactly the one implemented in ~gen from the book and want understand how that works based on current literature and move from there.

Gosh… at risk of a pun, that’s rather Demand-ing

The clock speed in the gen~ image is 8 Hz, which is well within reach of control rate. I think this shift register would not be difficult at control rate.

At audio rate, maybe the Feedback quark could handle it. If not, then it would require the equivalent of Pd’s block~ object, which doesn’t exist in SC and would require a fair amount of work on the C++ side, which isn’t going to happen in time for a satisfactory answer in this thread

hjh

[dietcv]

thanks for your reply, i have already started my C++ journey, this will take some time, meet me at the other end, haha

[jamshark70]

kr version:

(
~shiftRegister = { |rate = 8, prob = 0.3|
    var prev = LocalIn.kr(1, 0);
    var trig = Impulse.kr(rate);
    var oneBitNoise = WhiteNoise.kr.abs < prob;
    var nextPossibleValue = (prev * 2 + oneBitNoise) % 256;
    var next = Latch.kr(nextPossibleValue, trig);
    LocalOut.kr(next);
    SendReply.kr(trig, '/shift', next, prev);
    Silent.ar(1);
}.play;

OSCdef(\printBinary, { |msg|
    msg[3].asInteger.asBinaryDigits(8).postln
}, '/shift', s.addr);
)

~shiftRegister.release;

And while looking at that, I realized that this specific case could be done at audio rate, with a trick (just prevent the value from changing when the trigger is 0).

(
~shiftRegister = { |rate = 8, prob = 0.3|
    var prev = LocalIn.ar(1, 0);
    var trig = Impulse.ar(rate);
    var oneBitNoise = WhiteNoise.ar.abs < prob;
    var oneSample = oneBitNoise * trig;
    var shift = trig + 1;
    var nextPossibleValue = (prev * shift + oneSample) % 256;
    var next = Latch.ar(nextPossibleValue, trig);
    LocalOut.ar(next);
    SendReply.ar(trig, '/shift', next, prev);
    Silent.ar(1);
}.play;

OSCdef(\printBinary, { |msg|
    msg[3].asInteger.asBinaryDigits(8).postln
}, '/shift', s.addr);
)

~shiftRegister.release;

This isn’t true single sample feedback – you wouldn’t be able to run it at speeds greater than ControlRate – but the Max gen~ example isn’t running that fast either.

BTW I just noticed that the gen~ example in the picture includes a bug, which I fixed in my synth function.

@dietcv

Im not sure how the Latch Ugen could be implemented in the single sample feedback path in SC.

To my knowledge, it can’t. Dbufrd/wr for single-sample feedback works with demand-rate operations only. This includes math operators and other D units. It does not include ar units, because ar units have to calculate the full control block’s worth of samples Right Now.

Re: C++ side, probably the easiest approach would be one of: a/ extend SynthDef to specify up/down-sampling and/or block size, or b/ add a s_blocknew command to run a SynthDef with up/down-sampling and/or a different block size. Keeping the synth node as the basic unit of synthesis would simplify the dev side, and shift some usage burden onto the user.

I could also imagine something like:

SynthDef(\x, { |out|
	var src = In.ar(out, 1);

	var blocked = BlockSize.ar(src, 1);
	... do stuff...
	var sig = Unblock.ar(blocked);

	ReplaceOut.ar(out, sig);
});

… but that would be a bigger architectural change (and I can also already imagine complications…).

hjh

[dietcv]

thank you very much for taking the time.

@jamshark70

BTW I just noticed that the gen~ example in the picture includes a bug, which I fixed in my synth function.

which bug have you found?

@jamshark70

To my knowledge, it can’t. Dbufrd/wr for single-sample feedback works with demand-rate operations only.

yes, i think its the same for ~gen but there are a few more operators like “latch” available for working on a sample by sample level.

@jamshark70

… but that would be a bigger architectural change (and I can also already imagine complications…).

yeah, i think single sample feedback comes up from time to time here on the forum and there is no such solution like ~gen available in SC atm. Maybe instead of wanting to include Ugens in a single sample feedback path it would also an option to enlarge the palette of operators and demand ugens which you could use in that context for example something like “Dclutch”.

[dscheiba]

That is indeed an interesting problem - it looks easy but the implementation is not so easy.

I think I came up with a solution which does not need to rely on a feedback loop but instead introduces an additional hidden state which is used to feed in information - simply don’t forget your current state if you are in the spotlight and once you are shifted behind the curtain, forget everything you ever knew

Consumes only 35% of CPU on an i9… - why?

(
Ndef(\bitter, {
	// clock or outside impulse - can be audio rate :)
	var speed = \speed.kr(1.0);
	var impulse = Impulse.ar(speed);
	
	// number of bits to use as storage
	var bits = 8;
	
	// to avoid feedback simply shift the array by one
	// and update the value that is out of focus which
	// allows to introduce new information into the system
	var bitsToKeep = bits + 1;
	
	// count each impulse which will determine the
	// "out of focus"/hidden bit
	var hiddenBit = Integrator.ar(impulse);
	
	// calculate internal state which will be static except for
	// the inactive bit which samples from White Noise
	var internalSig = bitsToKeep.collect({|i|
		// @todo this is hacky but due floating point arithmetics necessary?
		var isInactive = (((hiddenBit%bitsToKeep) - i).abs < 0.1);
		// sample only if bit is inactive
		// maybe introduce some skewness that allows to skip mutation
		Latch.ar(WhiteNoise.ar, isInactive * impulse);
	});
	
	// now output the internal state, but shifted by the hidden bit
	// which will be omitted from the signal to output
	var sig = bits.collect({|i|
		// 
		Select.ar((i + hiddenBit) % bitsToKeep, internalSig);
	});
	(hiddenBit%bitsToKeep).poll(1.0, label: "hiddenBit");
	
	sig.poll(1.0, label: "sig");
});
)

(
Ndef(\bitterSound, {
	// assuming 8 bits
	var bits = Ndef.ar(\bitter, numChannels: 8);
	
	Splay.ar(bits.collect({|bit, i|
		SinOsc.ar(400.0 + (400*i)) * bit.range(0, 1) * Decay.ar(
			in: Impulse.ar(4.0),
			decayTime: 0.6,
		);
	})).tanh * \amp.kr(0.3);
	
}).play;
)

Ndef(\bitter).fadeTime = 4.0;

Ndef(\bitter).xset(\speed, 10.0);
Ndef(\bitter).xset(\speed, 15.0);
Ndef(\bitter).xset(\speed, 25.0);
Ndef(\bitter).xset(\speed, 100.0);
// am too fast => noise signal leaks
Ndef(\bitter).xset(\speed, 10000.0);
// slam on the bbbbbreaaak
Ndef(\bitter).xset(\speed, 1.0);
Ndef(\bitter).xset(\speed, 0.0);

Ndef(\bitterSound).stop(fadeTime: 4.0);

(
Ndef(\bitterScan, {
	// assuming 8 bits
	var bits = Ndef.ar(\bitter, numChannels: 8);
	
	SelectX.ar(
		// different start points for stereo
		which: Phasor.ar(rate: \rate.kr(0.01), start: [0.0, 0.5], end: bits.size),
		array: bits,
	).tanh * \amp.kr(0.3);
}).play;
)

Ndef(\bitterScan).fadeTime = 4.0;

Ndef(\bitter).xset(\speed, 1.0);
Ndef(\bitter).xset(\speed, 10.0);

// sounds a bit like some afx syro sound?
Ndef(\bitterScan).xset(\rate, 0.06);

// go faster
Ndef(\bitter).xset(\speed, 25.0);
// and slower
Ndef(\bitterScan).xset(\rate, 0.02);

// and vice verso
(
Ndef(\bitter).xset(\speed, 10.0);
Ndef(\bitterScan).xset(\rate, 0.2);
)

// stop phasing
Ndef(\bitterScan).xset(\rate, 0.0);
// only dc modulation now

// stop bitter
Ndef(\bitter).xset(\speed, 0.0);

Ndef.clear;

[jamshark70]

@dietcv

which bug have you found?

On second thought, I got a little overexcited – the “bug” is something that could never happen (although it could happen in a different context).

I’m tempted to do as some math books do, though, and “leave it as an exercise for the reader.” But (changed my mind at lunchtime)… If you mod an arbitrary integer by 256, the result could be 0 to 255. If there’s subsequently a possibility of adding 1, then the output could reach 256, no longer an 8 bit integer. So I thought (and still think) it’s better to compute the new value and mod last.

What I hadn’t thought through thoroughly (English spelling ) is that it isn’t an arbitrary integer – it’s guaranteed to be an even integer, which mod 256 could be at most 254. Adding 1 is then no problem. So then it becomes a matter of style preference. I like it better to do the mod last (seems safer to me to enforce an output range and then not do anything else), but in this specific case, you can get away with the other way.

@dscheiba

Consumes only 35% of CPU on an i9… - why?

There’s nothing in your code that requires so much CPU. I get about 4%.

The server’s CPU readings depend on a lot of factors, only one of which is the amount of calculation being done. It’s simply a measurement of the time it took to iterate over all the UGens, divided by the time between hardware blocks. E.g., if you’re running at 44.1 kHz with a 512-sample hardware buffer, each hardware buffer is ~11.6 ms. If the active UGens in a particular cycle required 2 ms to complete, then SC would report 17.2% CPU usage (roughly – this is also smoothed out by a moving average).

But the time it takes to compute also depends, for instance, on clock speed. Depending on CPU governing settings, the CPU can “downshift” to a slower speed if it isn’t “busy enough.” If that happens, then UGen calculation will take longer and you will see “more” CPU usage, even though the number of operations didn’t change. Conversely, when I’m running on battery power in “powersave” mode, I quite often see server CPU increasing up to a certain point, and then suddenly dropping by a factor of 2 or 3 when the system cranks up the clock speed. (“Performance” governor onstage, of course.)

Also, in Linux, the CPU reading is the total DSP time for all JACK apps, not only SC. This is useful as a measurement of “how close am I to getting xruns” but not useful as a measure of SC’s CPU usage.

Long story short, CPU % as reported by the server is, by itself, not a reliable benchmark.

hjh

[Sam_Pluta]

A solution using Delay1 instead of feedback:

(
    {
        |rate = 6, prob = 0.3|
        var trig = DelayN.ar(Impulse.ar(rate), 1, 1/rate);
        var val = TWChoose.ar(trig, DC.ar([0,1]), [1-prob, prob]);
        var del=val, sum;
        val = [val].addAll(7.collect{|i| del = Latch.ar(Delay1.ar(del),trig); del});
        sum = Mix(val*8.collect({|i| 2.pow(i)}));
        Poll.ar(Impulse.ar(rate), sum);
        nil
    }.play
)

or

(
    var registers = 16;
    {
        |rate = 6, prob = 0.3|
        var trig = DelayN.ar(Impulse.ar(rate), 1, 1/rate);
        var val = TWChoose.ar(trig, DC.ar([0,1]), [1-prob, prob]);
        var del=val, sum;
        val = [val].addAll((registers-1).collect{|i| del = Latch.ar(Delay1.ar(del),trig); del});
        sum = Mix(val*registers.collect({|i| 2.pow(i)}));
        Poll.ar(Impulse.ar(rate), sum);
        nil
    }.play
)

The advantage here is that it will run at full audio rate if necessary.

Sam

[dietcv]

thanks alot for all the contributions, beside these i have found a really clean demand attempt for a 4bit LFSR by redFrik on the web, which possibly could be adjusted to 8bits and adjusted with the limiting, extraction, rotation and inversion ideas from the book?

(
var lfsr4 = { |trig, iseed|
	var buf = LocalBuf(1).set(iseed);
	var b = Demand.ar(trig, 0, Dbufrd(buf));
	var output = b.bitAnd(1).bitXor(b.bitAnd(2).rightShift(1));
	b = b.rightShift(1).bitOr(output.leftShift(3));
	Demand.ar(trig, 0, Dbufwr(b, buf));
	b;
};

var lfsr = { |freq, iseed|
	var trig = Impulse.ar(freq);
	var lfsr = lfsr4.(trig, iseed).poll(trig, label: \integers);
	var shift = [
		lfsr.bitAnd(8).rightShift(3),
		lfsr.bitAnd(4).rightShift(2),
		lfsr.bitAnd(2).rightShift(1),
		lfsr.bitAnd(1)
	];
	Demand.ar(Impulse.ar(freq * 4), 0, Dseq(shift, inf)).poll(trig, label: \gates);
};

{
	lfsr.(\freq.kr(4), \iseed.kr(2r1000));
	Silent.ar;
}.play;
)

[dietcv]

@jamshark70

But (changed my mind at lunchtime)…

im glad you changed your mind, thanks for the explanation.

@dscheiba

Consumes only 35% of CPU on an i9… - why?

its also only 3-4% CPU on my machine.

[dietcv]

I think beside Dclutch, Dintegrate which accumulates the prior and the current value would also be nice.

[jamshark70]

@dietcv

Dintegrate

Dseries is an integrator, like Pseries is.

hjh

[dietcv]

thanks for clarifying!

[mjsyts]

You can use my LFSRNoise Ugen:

https://github.com/mjsyts/LFSRNoiseUGens

[dietcv]

What kind of Shift Register have you implemented? Is there some documentation?

[mjsyts]

Yes. It’s a XOR LFSR. The documentation is included in the Ugen folder as an accompanying help file (an external with documentation? crazy, right?)

[dietcv]

cant find it though

[mjsyts]

Ack. I think I had it set to a private repo. Check again, please and thank you!