A collection of unit shapers

[dietcv]

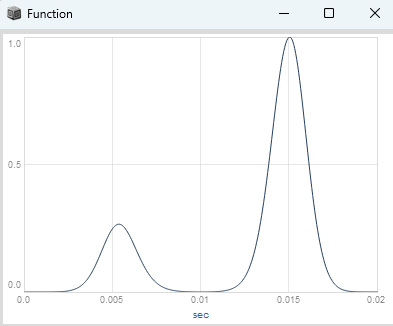
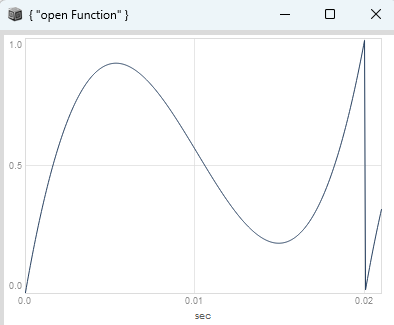
hey, here is a collection of unit shapers (they are still work in progress, i will add some other functions in the upcoming days). All the params used for these functions are nicely normalized between 0 and 1 and can be modulated at audio rate. To use them you need a ramp signal between 0 and 1 to drive them and the ProtoDef class by @elgiano GitHub - elgiano/ProtoDef: Prototyping classes for SuperCollider.

Maybe there could be a better way to organize those in a dictionary, but im mainly using this ProtoDef class for event prototyping and im focused on dsp rather then on these programming aspects, so if somebody knows a way to organize them which will be more accesible for others without that class let me know.

Some of these functions are straight forward and you can directly see their use case while others might not be as accessible on first sight. But I willl add more examples in the upcoming days, where you can see a possible use case.

update: added cubic seat and elliptic seat to linear morph and adjusted a few other things

update 2: implemented a general solution for the easing functions (also renamed some functions easeInOut is sigmoid while easeOutIn is seat). Now you could add additional easing cores. I have dervied the tukey window from the trapezoidal window with an additional duty param now (which shows that you can use any shaping function for the taper)

update 3: added a height param for easeInOut

update 4: implemented the linear interpolation of easing functions into the helping functions

update 5: added pseudoExponential easing (similiar to octic), adjusted a few variable names and descriptions

update 6: added OnePole filters

update 7: updated the easeInOut / easeOutIn functions with adjustable offset / height and included step, smoothStep and smootherStep for interpolation

(
ProtoDef(\unitShapers) {

	~init = { |self|

		self.helperFunctions = IdentityDictionary.new();
		self.unitShapers = IdentityDictionary.new();
		self.onePoleFilters = IdentityDictionary.new();
		self.waveShapers = IdentityDictionary.new();
		self.easingFunctions = IdentityDictionary.new();
		self.interpFunctions = IdentityDictionary.new();
		self.windowFunctions = IdentityDictionary.new();

		self.getHelperFunctions;
		self.getUnitShapers;
		self.getOnePoleFilters;
		self.getWaveShapers;
		self.getEasingFunctions;
		self.getInterpFunctions;
		self.getWindowFunctions;

	};

	~getHelperFunctions = { |self|

		// transfer functions
		var triangle = { |phase, skew|
			var warpedPhase = Select.ar(BinaryOpUGen('>', phase, skew), [
				phase / skew,
				1 - ((phase - skew) / (1 - skew))
			]);
			Select.ar(BinaryOpUGen('==', skew, 0), [warpedPhase, 1 - phase]);
		};

		var kink = { |phase, skew|
			var warpedPhase = Select.ar(BinaryOpUGen('>', phase, skew), [
				0.5 * (phase / skew),
				0.5 * (1 + ((phase - skew) / (1 - skew)))
			]);
			Select.ar(BinaryOpUGen('==', skew, 0), [warpedPhase,  0.5 * (1 + phase)]);
		};

		// interpolation of easing functions
		var interpEasing = { |x, shape, easingFuncA, easingFuncB, interp = \step|

			var interpFunc = case
			{ interp == \step } {
				var step = { |x|
					x;
				};
				step;
			}
			{ interp == \smoothStep } {
				var smoothStep = { |x|
					x * x * (3 - (2 * x));
				};
				smoothStep;
			}
			{ interp == \smootherStep } {
				var smootherStep = { |x|
					x * x * x * (x * (6 * x - 15) + 10);
				};
				smootherStep;
			};

			var easingToLinear = { |x, shape, easingFunc, interpFunc|
				var mix = shape * 2;
				var mixInterp = interpFunc.(mix);
				easingFunc * (1 - mixInterp) + (x * mixInterp);
			};

			var linearToEasing = { |x, shape, easingFunc, interpFunc|
				var mix = (shape - 0.5) * 2;
				var mixInterp = interpFunc.(mix);
				x * (1 - mixInterp) + (easingFunc * mixInterp);
			};

			Select.ar(BinaryOpUGen('>', shape, 0.5), [
				easingToLinear.(x, shape, easingFuncA, interpFunc),
				linearToEasing.(x, shape, easingFuncB, interpFunc)
			]);
		};

		// scale modulation depth of modulators between 0 and 1
		var modScale = { |modulator, value, amount, mode = \bipolar, direction = \full|

			// Convert bipolar to unipolar if needed
			var mod = if(mode == \bipolar) { (modulator + 1) * 0.5 } { modulator };

			case
			// Full range modulation
			{ direction == \full } {
				value * (1 - amount) + (mod * amount);
			}
			// Upward only modulation
			{ direction == \up } {
				value + (mod * (1 - value) * amount);
			}
			// Downward only modulation
			{ direction == \down } {
				value - (mod * value * amount);
			};

		};

		var modScaleBipolar = { |modulator, value, amount, direction = \center|
			modScale.(modulator, value, amount, \bipolar, direction);
		};


		var modScaleUnipolar = { |modulator, value, amount, direction = \center|
			modScale.(modulator, value, amount, \unipolar, direction);
		};

		self.helperFunctions.put(\triangle, triangle);
		self.helperFunctions.put(\kink, kink);

		self.helperFunctions.put(\interpEasing, interpEasing);

		self.helperFunctions.put(\modScaleBipolar, modScaleBipolar);
		self.helperFunctions.put(\modScaleUnipolar, modScaleUnipolar);

	};

	~getUnitShapers = { |self|

		var unitHanning = { |phase|
			1 - cos(phase * pi) * 0.5;
		};

		var unitCircular = { |phase|
			sqrt(phase * (2 - phase));
		};

		var unitWelch = { |phase|
			1 - squared(phase - 1);
		};

		var unitRaisedCos = { |phase, index|
			var cosine = cos(phase * pi);
			exp(index.abs * (cosine.neg - 1));
		};

		var unitGaussian = { |phase, index|
			var cosine = cos(phase * 0.5pi) * index;
			exp(cosine * cosine.neg);
		};

		var unitTrapezoid = { |phase, width, duty = 1|
			var sustain = 1 - width;
			var offset = phase - (1 - duty);
			var trapezoid = (offset / sustain + (1 - duty)).clip(0, 1);
			var pulse = offset > 0;
			Select.ar(BinaryOpUGen('==', width, 1), [trapezoid, pulse]);
		};

		var unitTukey = { |phase, width, duty = 1|
			var trapezoid = unitTrapezoid.(phase, width, duty);
			unitHanning.(trapezoid);
		};
		
		self.unitShapers.put(\hanning, unitHanning);
		self.unitShapers.put(\circular, unitCircular);
		self.unitShapers.put(\welch, unitWelch);
		self.unitShapers.put(\raisedCos, unitRaisedCos);
		self.unitShapers.put(\gaussian, unitGaussian);
		self.unitShapers.put(\trapezoid, unitTrapezoid);
		self.unitShapers.put(\tukey, unitTukey);

	};

	~getOnePoleFilters = { |self|

		var lowpass = { |sig, slope|
			var safeSlope = slope.clip(-0.5, 0.5);
			OnePole.ar(sig, exp(-2pi * safeSlope.abs));
		};

		var highpass = { |sig, slope|
			sig - lowpass.(sig, slope);
		};

		self.onePoleFilters.put(\lpf, lowpass);
		self.onePoleFilters.put(\hpf, highpass);

	};

	~getWaveShapers = { |self|

		var sigmoid = { |x, curve|
			var safeDenom = max(1 - curve, 0.0001);
			var k = 2 * curve / safeDenom;
			(1 + k) * x / (1 + (k * x.abs));
		};

		self.waveShapers.put(\sigmoid, sigmoid);

	};

	~getEasingFunctions = { |self|

		var easingCores = [
			\cubic,
			\quintic,
			\sine,
			\circular,
			\pseudoExp,
			\pseudoLog2
		];

		easingCores.do{ |key|

			var easeIn = case
			{ key == \cubic } {
				var cubicIn = { |x|
					x * x * x;
				};
				cubicIn;
			}
			{ key == \quintic } {
				var quinticIn = { |x|
					x * x * x * x * x;
				};
				quinticIn;
			}
			{ key == \sine } {
				var sineIn = { |x|
					1 - cos(x * 0.5pi);
				};
				sineIn;
			}
			{ key == \circular } {
				var circularIn = { |x|
					1 - sqrt(1 - (x * x));
				};
				circularIn;
			}
			{ key == \pseudoExp } {
				var pseudoExpIn = { |x, coef = 13|
					(2 ** (coef * x) - 1) / (2 ** coef - 1)
				};
				pseudoExpIn;
			}
			{ key == \pseudoLog2 } {
				var pseudoLog2In = { |x, coef = 12.5|
					1 - (log2((1 - x) * (2 ** coef - 1) + 1) / coef);
				};
				pseudoLog2In;
			};

			var easeOut = { |x|
				1 - easeIn.(1 - x);
			};

			// sigmoid with variable offset
			var easeInOut = { |x, offset = 0.5|
				Select.ar(x > offset, [
					offset * easeIn.(x / offset),
					offset + ((1 - offset) * (1 - easeIn.((1 - x) / (1 - offset))))
				]);
			};

			// seat with variable height
			var easeOutIn = { |x, height = 0.5|
				Select.ar(x > height, [
					height * (1 - easeIn.((height - x) / height)),
					height + ((1 - height) * easeIn.((x - height) / (1 - height)))
				]);
			};

			self.easingFunctions.put("%In".format(key).asSymbol, easeIn);
			self.easingFunctions.put("%Out".format(key).asSymbol, easeOut);
			self.easingFunctions.put("%Sigmoid".format(key).asSymbol, easeInOut);
			self.easingFunctions.put("%Seat".format(key).asSymbol, easeOutIn);

		};

	};

	~getInterpFunctions = { |self|

		// linear interpolation of quintic in and quintic out
		var quinticInterp = { |x, shape, interp = \step|
			var easeOut = self.easingFunctions[\quinticOut].(x);
			var easeIn = self.easingFunctions[\quinticIn].(x);
			self.helperFunctions[\interpEasing].(x, shape, easeOut, easeIn, interp);
		};

		// linear interpolation of exponential in and exponential out
		var pseudoExpInterp = { |x, shape, interp = \step|
			var easeOut = self.easingFunctions[\pseudoExpOut].(x);
			var easeIn = self.easingFunctions[\pseudoExpIn].(x);
			self.helperFunctions[\interpEasing].(x, shape, easeOut, easeIn, interp);
		};

		// linear interpolation of quintic sigmoid to quintic seat
		var sigmoidToSeatInterp = { |x, shape, inflection = 0.5, interp = \step|
			var easeOut = self.easingFunctions[\quinticSigmoid].(x, inflection);
			var easeIn = self.easingFunctions[\quinticSeat].(x, inflection);
			self.helperFunctions[\interpEasing].(x, shape, easeOut, easeIn, interp);
		};

		self.interpFunctions.put(\quintic, quinticInterp);
		self.interpFunctions.put(\exponential, pseudoExpInterp);
		self.interpFunctions.put(\sigmoidToSeat, sigmoidToSeatInterp);

	};

	~getWindowFunctions = { |self|

		var hanningWindow = { |phase, skew|
			var warpedPhase = self.helperFunctions[\triangle].(phase, skew);
			self.unitShapers[\hanning].(warpedPhase);
		};

		var circularWindow = { |phase, skew|
			var warpedPhase = self.helperFunctions[\triangle].(phase, skew);
			self.unitShapers[\circular].(warpedPhase);
		};

		var welchWindow = { |phase, skew|
			var warpedPhase = self.helperFunctions[\triangle].(phase, skew);
			self.unitShapers[\welch].(warpedPhase);
		};

		var raisedCosWindow = { |phase, skew, index|
			var warpedPhase = self.helperFunctions[\triangle].(phase, skew);
			var raisedCos = self.unitShapers[\raisedCos].(warpedPhase, index);
			var hanning = self.unitShapers[\hanning].(warpedPhase);
			raisedCos * hanning;
		};

		var gaussianWindow = { |phase, skew, index|
			var warpedPhase = self.helperFunctions[\triangle].(phase, skew);
			var gaussian = self.unitShapers[\gaussian].(warpedPhase, index);
			var hanning = self.unitShapers[\hanning].(warpedPhase);
			gaussian * hanning;
		};

		var trapezoidalWindow = { |phase, skew, width, duty = 1|
			var warpedPhase = self.helperFunctions[\triangle].(phase, skew);
			self.unitShapers[\trapezoid].(warpedPhase, width, duty);
		};

		var tukeyWindow = { |phase, skew, width, duty = 1|
			var warpedPhase = self.helperFunctions[\triangle].(phase, skew);
			self.unitShapers[\tukey].(warpedPhase, width, duty);
		};

		var exponentialWindow = { |phase, skew, shape, interp = \step|
			var warpedPhase = self.helperFunctions[\triangle].(phase, skew);
			self.interpFunctions[\exponential].(warpedPhase, 1 - shape, interp);
		};

		self.windowFunctions.put(\hanning, hanningWindow);
		self.windowFunctions.put(\circular, circularWindow);
		self.windowFunctions.put(\welch, welchWindow);
		self.windowFunctions.put(\raisedCos, raisedCosWindow);
		self.windowFunctions.put(\gaussian, gaussianWindow);
		self.windowFunctions.put(\tukey, tukeyWindow);
		self.windowFunctions.put(\trapezoid, trapezoidalWindow);
		self.windowFunctions.put(\exponential, exponentialWindow);

	};

};
)

~unitShapers = Prototype(\unitShapers);


// warped triangle

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);
	~unitShapers.helperFunctions[\triangle].(phase, \skew.kr(0.5));
}.plot(0.02);
)

// warped hanning window

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);
	~unitShapers.windowFunctions[\hanning].(phase, \skew.kr(0.5));
}.plot(0.02);
)

// warped welch window

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);
	~unitShapers.windowFunctions[\welch].(phase, \skew.kr(0.5));
}.plot(0.02);
)

// warped circular window

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);
	~unitShapers.windowFunctions[\circular].(phase, \skew.kr(0.5));
}.plot(0.02);
)

// warped raised cosine window

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);
	~unitShapers.windowFunctions[\raisedCos].(phase, \skew.kr(0.5), \index.kr(5));
}.plot(0.02);
)

// warped gaussian window

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);
	~unitShapers.windowFunctions[\gaussian].(phase, \skew.kr(0.5), \index.kr(5));
}.plot(0.02);
)

// warped trapezoidal window

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);
	~unitShapers.windowFunctions[\trapezoid].(phase, \skew.kr(0.5), \width.kr(0.5), \duty.kr(0.25));
}.plot(0.02);
)

// warped tukey window

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);
	~unitShapers.windowFunctions[\tukey].(phase, \skew.kr(0.5), \width.kr(0.5), \duty.kr(1));
}.plot(0.02);
)

// warped exponential window

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);

	var sigA = ~unitShapers.windowFunctions[\exponential].(phase, \skew.kr(0.5), \shape.kr(0.4), \step);
	var sigB = ~unitShapers.windowFunctions[\exponential].(phase, \skew.kr(0.5), \shape.kr(0.4), \smoothStep);
	var sigC = ~unitShapers.windowFunctions[\exponential].(phase, \skew.kr(0.5), \shape.kr(0.4), \smootherStep);

	[sigA, sigB, sigC];
}.plot(0.02).superpose_(true).plotColor_([Color.red, Color.blue, Color.magenta]);
)

///////////////////////////////////////////////////////////////////////////////

// easing functions:

// test interpolation

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);

	var sigA = ~unitShapers.interpFunctions[\exponential].(phase, \shapeA.kr(0.7), \step);
	var sigB = ~unitShapers.interpFunctions[\exponential].(phase, \shapeB.kr(0.7), \smoothStep);
	var sigC = ~unitShapers.interpFunctions[\exponential].(phase, \shapeC.kr(0.7), \smootherStep);

	[sigA, sigB, sigC];
}.plot(0.02).superpose_(true).plotColor_([Color.red, Color.blue, Color.magenta]);
)


// linear interpolation of exponential in and out

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);

	var sigA = ~unitShapers.interpFunctions[\exponential].(phase, \shapeA.kr(0));
	var sigB = ~unitShapers.interpFunctions[\exponential].(phase, \shapeB.kr(0.5));
	var sigC = ~unitShapers.interpFunctions[\exponential].(phase, \shapeC.kr(1));

	[sigA, sigB, sigC];
}.plot(0.02).superpose_(true).plotColor_([Color.red, Color.blue, Color.magenta]);
)

///////////////////////////////////////////////////////////////////////////////

// easing functions:

// linear interpolation of quintic sigmoid to quintic seat (variable shape)

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);

	var sigA = ~unitShapers.interpFunctions[\sigmoidToSeat].(phase, \shapeA.kr(0), \inflection.kr(0.5));
	var sigB = ~unitShapers.interpFunctions[\sigmoidToSeat].(phase, \shapeB.kr(0.5), \inflection.kr(0.5));
	var sigC = ~unitShapers.interpFunctions[\sigmoidToSeat].(phase, \shapeC.kr(1), \inflection.kr(0.5));

	[sigA, sigB, sigC];
}.plot(0.02).superpose_(true).plotColor_([Color.red, Color.blue, Color.magenta]);
)

// linear interpolation of quintic sigmoid to quintic seat (variable inflection)

(
{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);

	var sigA = ~unitShapers.interpFunctions[\sigmoidToSeat].(phase, \shapeA.kr(0), \inflectionA.kr(0.25));
	var sigB = ~unitShapers.interpFunctions[\sigmoidToSeat].(phase, \shapeB.kr(0.5), \inflectionB.kr(0.50));
	var sigC = ~unitShapers.interpFunctions[\sigmoidToSeat].(phase, \shapeC.kr(1), \inflectionC.kr(0.75));

	[sigA, sigB, sigC];
}.plot(0.02).superpose_(true).plotColor_([Color.red, Color.blue, Color.magenta]);
)

[dietcv]

hey, i found a nice way to generalize all the easing functions, if the easing core is equal to easeIn (completely restructured the elliptic easing for this) the different functions always output the correct results. So instead of declaring the different functions for every easing core i would like to iterate over the easing cores and declare all the other functions and put them in the identity dictionary. I only know how to put them in the dictionary with the correct key using "%In".format(easingCore).asSymbol when iterating over an array of keys. Could someone help me to iterate over the core functions and put each of the other functions in the dictionary at their specific key? Or is there a better way? thanks

// easing cores

var cubic = { |x|
	x * x * x;
};

var quintic = { |x|
	x * x * x * x * x;
};

var elliptic = { |x|
	1 - sqrt(1 - (x * x));
};

// easing functions

[\cubic, \quintic, \elliptic].do{ |easingCore, i|
	
	var easeIn = { |x|
		easingCore.(x);
	};

	var easeOut = { |x|
		1 - easingCore.(1 - x);
	};

	var easeInOut = { |x|
		Select.ar(x > 0.5, [
			easingCore.(2 * x) * 0.5,
			1 - (easingCore.(2 * (1 - x)) * 0.5)
		]);
	};

	var easeSeat = { |x, height = 0.5|
		Select.ar(x > 0.5, [
			height - (height * easingCore.(1 - (x * 2))),
			height + ((1 - height) * easingCore.((x - 0.5) * 2))
		]);
	};

	var easeSeatWarped = { |phase, skew = 0.5, height = 0.5|
		var warpedPhase = self.helperFunctions[\kink].(phase, skew);
		easeSeat.(warpedPhase, height);
	};

	var easeSeatOut = { |x, height = 0.5|
		1 - easeSeat.(1 - x, height);
	};

	self.easingFunctions.put("%In".format(easingCore).asSymbol, easeIn);
	self.easingFunctions.put("%Out".format(easingCore).asSymbol, easeOut);
	self.easingFunctions.put("%InOut".format(easingCore).asSymbol, easeInOut);
	self.easingFunctions.put("%Seat".format(easingCore).asSymbol, easeSeat);
	self.easingFunctions.put("%SeatOut".format(easingCore).asSymbol, easeSeatOut);
	self.easingFunctions.put("%SeatWarped".format(easingCore).asSymbol, easeSeatWarped);

};

[dietcv]

maybe something like:

~getEasingFunctions = { |self|
	
	[\cubic, \quintic, \elliptic].do{ |key, i|
		
		var easeIn = case
		{ key == \cubic } {
			{ |x| x * x * x } 
		}
		{ key == \quintic } {
			{ |x| x * x * x * x * x } 
		}
		{ key == \elliptic } {
			{ |x| 1 - sqrt(1 - (x * x)) } 
		};
		
		var easeOut = { |x|
			1 - easeIn.(1 - x);
		};
		
		var easeInOut = { |x|
			Select.ar(x > 0.5, [
				easeIn.(2 * x) * 0.5,
				1 - (easeIn.(2 * (1 - x)) * 0.5)
			]);
		};
		
		var easeSeat = { |x, height = 0.5|
			Select.ar(x > 0.5, [
				height - (height * easeIn.(1 - (x * 2))),
				height + ((1 - height) * easeIn.((x - 0.5) * 2))
			]);
		};
		
		var easeSeatWarped = { |phase, skew = 0.5, height = 0.5|
			var warpedPhase = self.helperFunctions[\kink].(phase, skew);
			easeSeat.(warpedPhase, height);
		};
		
		var easeSeatOut = { |x, height = 0.5|
			1 - easeSeat.(1 - x, height);
		};
		
		self.easingFunctions.put("%In".format(key).asSymbol, easeIn);
		self.easingFunctions.put("%Out".format(key).asSymbol, easeOut);
		self.easingFunctions.put("%InOut".format(key).asSymbol, easeInOut);
		self.easingFunctions.put("%Seat".format(key).asSymbol, easeSeat);
		self.easingFunctions.put("%SeatOut".format(key).asSymbol, easeSeatOut);
		self.easingFunctions.put("%SeatWarped".format(key).asSymbol, easeSeatWarped);
	};
	
};

[dietcv]

used this implementation for now and made an update until someone has a better way of implementing that.
I think the morphing functions could also be generalized:
something like:

var easeOutToLinear = { |x, shape, easeOutFunc|
	var mix = shape * 2;
	var easeOut = easeOutFunc.(x);
	easeOut * (1 - mix) + (x * mix);
};

var linearToEaseIn = { |x, shape, easeInFunc|
	var mix = (shape - 0.5) * 2;
	var easeIn = easeInFunc.(x);
	x * (1 - mix) + (easeIn * mix);
};

var morphingFunc = { |x, shape|
	Select.ar(shape > 0.5, [
		easeOutToLinear.(x, shape),
		linearToEaseIn.(x, shape)
	]);
};

[dietcv]

I have made another update, where i updated the easeInOut function to have an additional height argument.

In some formulas online you find two parameters to control a and b for either easeInOut (sigmoid) and easeOutIn (seat).

Circular & Elliptical Shaping Functions - Golan Levin and Collaborators

The core concept of these different functions for me is to build everything from small independent building blocks which can be combined as you like, so i left out the a param for all these functions because you can always get it by warping the phase with the kink transfer function for either of these functions.
For the case of the easeInOut function you can get a smooth transition from the in to the out segment when skew and hight have the same values:

(
var circularIn = { |x|
    1 - sqrt(1 - (x * x));
};
var circularInOut = { |x, height|
    Select.ar(x > 0.5, [
        height * circularIn.(x * 2),
        height + ((1 - height) * (1 - circularIn.(2 * (1 - x))))
    ]);
};
var kink = { |phase, skew|
    Select.ar(phase > skew, [
        0.5 * (phase / skew),
        0.5 * (1 + ((phase - skew) / (1 - skew)))
    ]);
};

{
    var phase = Phasor.ar(0, 50 * SampleDur.ir);
	var warpedPhase = kink.(phase, \skew.kr(0.75));
	circularInOut.(warpedPhase, \height.kr(0.75));
}.plot(0.02);
) 

[jordan]

@dietcv

Maybe there could be a better way to organize those in a dictionary, but im mainly using this ProtoDef class for event prototyping and im focused on dsp rather then on these programming aspects, so if somebody knows a way to organize them which will be more accesible for others without that class let me know.

At some point, writing your own class becomes much easier and cleaner. For me, this is beyond the complexity I’m comfortable with when using protoobjects.

[dietcv]

i have made another update, where i have implemented the linear interpolation of easing functions into the helping functions

[dietcv]

thanks for your reply, i think im quite happy for now with the proto objects instead of writing classes

[Sam_Pluta]

but as classes it can be a quark, which would be a solid addition

[dietcv]

yeah, maybe thats a good idea I think i would need to add some additional things to feel comfortable releasing it as a quark.

[dietcv]

I have made another update with the adjustment of some variable names and added more descriptive descriptions. I guess thats it for now.

There are also more complex easing cores like bounce or elastic. But i think these should be composed out of simple building blocks, to keep everything modular and modulatable.

Just an example:

(
{
	var measurePhase, stepPhase, measureLFO, stepLFO;

	measurePhase = Phasor.ar(DC.ar(0), \rate.kr(50) * SampleDur.ir);
	stepPhase = (measurePhase * \stepsPerMeasure.kr(2)).wrap(0, 1);

	measureLFO = ~unitShapers.windowFunctions[\hanning].(measurePhase, \skewA.kr(0.75));
	stepLFO = ~unitShapers.windowFunctions[\gaussian].(stepPhase, \skewB.kr(0.5), \index.kr(2));

	stepLFO * measureLFO;

}.plot(0.02);
)

[dietcv]

derived cubic interpolation normalized between 0 and 1 from this desmos formula. Maybe thats also interesting.

Cubic Interpolation

(
var cubicInterpolation = { |x, index|
    (x * (1 + (index / 6))) +
    ((x * x) * (index.neg / 2)) +
    ((x * x * x) * (index / 3))
};

{
	var phase = Phasor.ar(0, 50 * SampleDur.ir);
	cubicInterpolation.(phase, \index.kr(40));
}.plot(0.021);
)

EDIT: the index limit is 48 to have the output normalized between 0 and 1

[dietcv]

Because all the params of the unit shapers are normalized between 0 and 1, i think i will add these modulator scalers to the helpingFunctions, to normalize the modDepth of an potential LFO also between 0 and 1.

var modScaleBipolar = { |bipolar, amount|
	(0.5 * amount * (bipolar - 1) + 1);
};

var modScaleUnipolar = { |unipolar, amount|
	1 - (amount * (1 - unipolar));
};

EDIT: i think the modulation should be centered around a value of 0.5 where for the linear easing interpolation is always the linear phase case and 0 the easeOut and 1 the easeIn. So a modulation amount of 0 should output 0.5 and a modulation amount of 1 should output mod values between 0 and 1.
Will think about a general formula once more (the formula above is great for amplitude modulation between 0 and 1, where mod amount of 0 means output of 1 where a mod amount of 1 means output between 0 and 1). Best would be to derive both from the same function with an additional argument and also add the case mod 0 means output 0 and mod 1 means output between 0 and 1.

So there are three cases for both of the functions (unipolar and bipolar):
center 0 and amount 0 → output 0
center 0 and amount 1 → output between 0 and 1

center 0.5 and amount 0 → output 0.5
center 0.5 and amount 1 → output between 0 and 1

center 1 and amount 0 → output 1
center 1 and amount 1 → output between 0 and 1

could imagine to have a target argument to both of the functions with options of \floor = 0, \center = 0.5 and \ceil = 1

[dietcv]

I think i have figured it out:

(
var modScaleBipolar = { |bipolar, amount, target|

	var base = case
	{ target == \floor } { K2A.ar(0) }
	{ target == \center } { K2A.ar(0.5) }
	{ target == \ceil } { K2A.ar(1) };

    base * (1 - amount) + (amount * (0.5 * (bipolar + 1)));
};

var modScaleUnipolar = { |unipolar, amount, target|

	var base = case
	{ target == \floor } { K2A.ar(0) }
	{ target == \center } { K2A.ar(0.5) }
	{ target == \ceil } { K2A.ar(1) };

    base * (1 - amount) + (amount * unipolar);
};

{
	var sig = SinOsc.ar(100);
	modScaleBipolar.(sig, 0.5, \floor);
}.plot(0.02);
)

[dietcv]

hey, i have updated the initial post:

• some minor adjustments for taking care of the edge cases where we are dividing by zero.These are based on BinaryOpUGen.
• added linear interpolation for bipolar / unipolar modulators for the modulation of normalized values between 0 and 1, where you could use a modDepth between 0 and 1 which is scaling the modulational amount and the output will always be between 0 and 1.
• added a tunable sigmoid for waveshaping

[dietcv]

i have updated the library, now you additionally find OnePole filters which calculate their coefficient based on a slope argument, which could then be used as a frequency tracking filter for FM/PM.

[dietcv]

I have investigated some different interpolation methods, you could adjust the linear interpolation of the easing functions witht this smoothStep function derived from a third order polynomial:

var interpEasing = { |x, shape, easingFuncA, easingFuncB|
	
	var smoothstep = { |x|
		x * x * (3 - (2 * x))
	};
	
	var easingToLinear = { |x, shape, easingFunc|
		var mix = smoothstep.(shape * 2);
		easingFunc * (1 - mix) + (x * mix);
	};
	
	var linearToEasing = { |x, shape, easingFunc|
		var mix = smoothstep.((shape - 0.5) * 2);
		x * (1 - mix) + (easingFunc * mix);
	};
	
	Select.ar(BinaryOpUGen('>', shape, 0.5), [
		easingToLinear.(x, shape, easingFuncA),
		linearToEasing.(x, shape, easingFuncB)
	]);
};

[dietcv]

I thought i would make a quark with pseudo ugens, but i think this will be my first c++ project.

[dietcv]

I have updated the library with easeInOut / easeOutIn functions with adjustable offset / height and included step, smoothStep and smootherStep for interpolation.