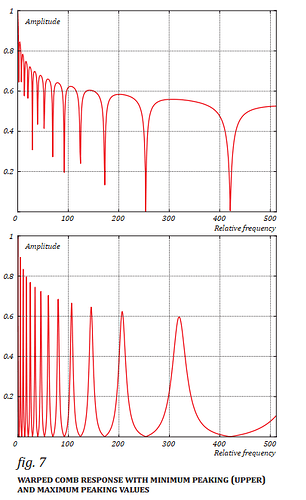
hey, i would like to share this additive synthesis approach with you, using an additive comb filter (its an additive-subtractive approach similiar to razor or harmor) with control over comb density, comb offset, comb skew and comb peak. Some of its initial ideas especially the function for detuning the partials (based on the bank piano model for detuning strings) are by @nathan. But i have reworked the additive comb filter which is now based on a raised cosine window and all params are nicely normalised between 0 and 1.
I have additionally added a spectral limiter, so you can modulate the fundamental frequency without getting any aliasing. Beside these amplitude transformers, i have added an additional frequency tranformer called warpFrequencies, based on a transfer function (a ramp with a kink at 0.5, think classic phase distortion) to compress the partials in the lower or upper part of the spectrum. Its a bit heavy on CPU if you use 128 partials, but if you set them on 64 its okay.
The modulation is just a proof of concept, you can adjust it to your liking.
(
var initChain = { |numPartials, freq|
(
freq: freq,
numPartials: numPartials,
ratios: (1..numPartials),
amps: 1 ! numPartials,
)
};
var makeStretchedHarmonicSeries = { |chain, inharmonicity|
chain[\freqs] = chain[\freq] * chain[\ratios] * (1 + (inharmonicity * chain[\ratios] * chain[\ratios])).sqrt;
chain;
};
var transferFunc = { |phase, skew|
Select.kr(phase > skew, [
0.5 * phase / skew,
0.5 * (1 + ((phase - skew) / (1 - skew)))
]);
};
var warpFrequencies = { |chain, warpPoint|
var normalizedFreqs = (chain[\freqs] / chain[\freqs][chain[\numPartials] - 1]).clip(0, 1);
var warpedFreqs = transferFunc.(normalizedFreqs, 1 - warpPoint);
chain[\freqs] = warpedFreqs * chain[\freqs][chain[\numPartials] - 1];
chain;
};
var addSpectralTilt = { |chain, tiltPerOctave|
chain[\amps] = chain[\amps] * (chain[\ratios].log2 * tiltPerOctave).dbamp;
chain;
};
var raisedCos = { |phase, index|
var cosine = cos(phase * 2pi);
var raised = exp(index.abs * (cosine - 1));
var hanning = 0.5 * (1 + cos(phase * 2pi));
raised * hanning;
};
var addCombFilter = { |chain, combOffset, combDensity, combSkew, combPeak|
var phase, warpedPhase;
phase = chain[\freqs].log2 - chain[\freq].log2;
phase = (phase * combDensity - combOffset).wrap(0, 1);
warpedPhase = transferFunc.(phase, combSkew);
chain[\amps] = chain[\amps] * raisedCos.(warpedPhase, combPeak);
chain;
};
var addLimiter = { |chain|
var nyquist = SampleRate.ir / 2 - 2000;
var fade = nyquist - 1000;
var limiter = 1 - ((chain[\freqs].clip(fade, nyquist) - fade) * 0.001);
chain[\amps] = chain[\amps] * limiter;
chain;
};
SynthDef(\additiveComb, {
var numPartials = 128;
var lfos, combOffset, combDensity, combPeak, combSkew, warpSpectrum, inharmonicity, freq, chain, sig;
lfos = 6.collect{ |i|
SinOsc.kr(\modMF.kr(0.5, spec: ControlSpec(0.1, 3)), Rand(0, 2pi));
};
combOffset = \combOffset.kr(0, spec: ControlSpec(0, 1));
combOffset = combOffset * (2 ** (lfos[0] * \combOffsetMD.kr(0, spec: ControlSpec(0, 2))));
combDensity = \combDensity.kr(0, spec: ControlSpec(0, 1));
combDensity = combDensity * (2 ** (lfos[1] * \combDensityMD.kr(0, spec: ControlSpec(0, 2))));
combPeak = \combPeak.kr(5, spec: ControlSpec(1, 10));
combPeak = combPeak * (2 ** (lfos[2] * \combPeakMD.kr(0, spec: ControlSpec(0, 2))));
combSkew = \combSkew.kr(0.5, spec: ControlSpec(0.01, 0.99));
combSkew = combSkew * (2 ** (lfos[3] * \combSkewMD.kr(0, spec: ControlSpec(0, 2))));
warpSpectrum = \warpSpec.kr(0.5, spec: ControlSpec(0, 1));
warpSpectrum = warpSpectrum * (2 ** (lfos[4] * \warpSpecMD.kr(0, spec: ControlSpec(0, 2))));
freq = \freq.kr(60, spec: ControlSpec(20, 500));
freq = freq * (2 ** (lfos[5] * \freqMD.kr(0, spec: ControlSpec(0, 3))));
inharmonicity = \inharmonicity.kr(0, spec: ControlSpec(0, 0.1));
/////////////////////////////////////////////////////////////////////////////
chain = initChain.(numPartials, freq);
chain = makeStretchedHarmonicSeries.(chain, inharmonicity);
chain = warpFrequencies.(chain, warpSpectrum);
chain = addLimiter.(chain);
chain = addSpectralTilt.(chain, \tiltPerOctaveDb.kr(-3, spec: ControlSpec(-3, -12)));
chain = addCombFilter.(chain, combOffset, combDensity, combSkew, combPeak);
sig = SinOsc.ar(
freq: chain[\freqs],
phase: { Rand(0, 2pi) } ! chain[\numPartials],
mul: chain[\amps]
);
sig = sig[0,2..].sum + ([-1,1] * sig[1,3..].sum);
sig = sig * -15.dbamp;
sig = sig * \amp.kr(-5, spec: ControlSpec(-5, -25, \lin, 1)).dbamp;
sig = sig * Env.asr(0.001, 1, 0.001).ar(Done.freeSelf, \gate.kr(1));
sig = Limiter.ar(sig);
sig = LeakDC.ar(sig);
Out.ar(\out.kr(0), sig);
}).add;
)
(
Routine({
s.bind {
Synth(\additiveComb, [
\freq, 110,
\freqMD, 0,
\inharmonicity, 0,
\modMF, 0.5,
\combOffset, 0,
\combOffsetMD, 0,
\combDensity, 0.5,
\combDensityMD, 1,
\combSkew, 0.5,
\combSkewMD, 0,
\combPeak, 5,
\combPeakMD, 0,
\warpSpec, 0.5,
\warpSpecMD, 0,
\tiltPerOctaveDb, -3.00,
\amp, -15,
\out, 0,
]);
};
}).play;
)