(Big Nested) Arrays: taking more and more time to compute when it should take less and less

Questions Code Review
1

I’m not good at computing large number of datas, and I ended up with a counter-intuitive result which I wasn’t able to diagnose, so I’m looking for help if you have any clue about this problem.

[context, skip here if needed]
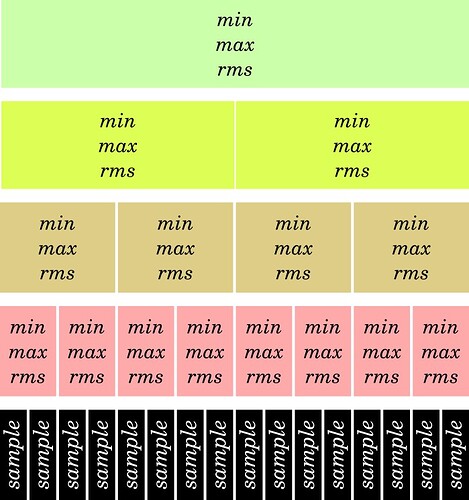
Here’s the context: I’m trying to mimic Audacity’s file view display, with min, max and rms for each ‘sound area’ a pixel covers.

A friend of mine told me that using dyadic rationals might be the fastest way to recompute min, max and rms for a new area. This saturates RAM with a lot of datas in exchange for less CPU usage. Visually:

dr
dr699×745 87.9 KB

For each power of 2 ‘samples areas’, we precalculate min, max and rms. When we need to find those data for a certain area, we find the biggest chunk that is located within the boundaries, then do the same on each extremities until it is filled. Then, we only need to calculate min, max and rms once with the least possible number of data.

[end of context, here’s the problem]
Anyway, I tried to generate those layers of data automatically, starting with 2 samples chunk, then constructing subsequent layers on top of the previous one. Each layers has half the number of data the previous one had: it should take half the time to compute. But that is not the case: it takes more and more time to compute less values! I think this has to do with pointers but I’m not sure.

Here is the code. But wait: only try it with a really small sound file. On my computer, a mono file lasting 300ms takes 45 sec to compute! A 4s stereo file never finishes computing and make SC laggy…

(
var getDRData = { |filePath|
	var soundFile = SoundFile.openRead(filePath);
	var array = FloatArray.newClear(
		soundFile.numFrames * soundFile.numChannels
	);
	var channels;
	var data = Array.newClear(soundFile.numChannels);
	var fileSize = soundFile.numFrames;
	var maxPow = 2;
	var nPow = 1;
	var sizes;
	var min, max, rms;
	var current, prev;
	soundFile.readData(array);
	soundFile.close;
	channels = array.unlace(soundFile.numChannels);
	while { 2.pow(nPow + 1) < fileSize } {
		nPow = nPow + 1;
	};
	sizes = Array.newClear(nPow);
	// Calculate array sizes
	nPow.do({ |pow|
		var remainder = fileSize % 2.pow(pow + 1);
		var size = (fileSize - remainder) / 2.pow(pow + 1);
		if(remainder > 0) {
			size = size + 1;
		};
		sizes[pow] = size.asInteger;
	});
	// Create place holders
	data.size.do({ |channel|
		data[channel] = Array.newClear(nPow + 1);
		nPow.do({ |index|
			data[channel][index + 1] = Array.newClear(sizes[index]);
		});
	});

	// Compute datas
	channels.do({ |channel, channelIndex|
		data[channelIndex][0] = channel;
		// 2 samples first
		data[channelIndex][1] = Array.newClear(sizes[0]);
		(data[channelIndex][1].size - 1).do({ |index|
			min = min(channel[index * 2], channel[(index * 2) + 1]);
			max = max(channel[index * 2], channel[(index * 2) + 1]);
			rms = (channel[index * 2].pow(2) + channel[(index * 2) + 1].pow(2)).sqrt;
			data[channelIndex][1][index] = [min, max, rms];
		});
		// Calculate last index
		if((channel.size % 2) == 0) {
			min = min(channel[channel.size - 2], channel.last);
			max = max(channel[channel.size - 2], channel.last);
			rms = (channel[channel.size - 2].pow(2) + channel.last.pow(2)).sqrt;
			data[channelIndex][1][data[channelIndex][1].size - 1] = [min, max, rms];
		} {
			data[channelIndex][1][data[channelIndex][1].size - 1] = Array.fill(3, { channel.last });
		};

		// HERE COMES THE TROUBLE:
		// Calculate other powers of 2:
		(nPow - 1).do({ |pow|
			"Power: ".post;
			2.pow(pow + 1).asInteger.postln;
			"Data number: ".post;
			data[channelIndex][pow + 2].size.postln;
			bench {
				(data[channelIndex][pow + 2].size - 1).do({ |index|
					min = min(
						data[channelIndex][pow + 1][index * 2],
						data[channelIndex][pow + 1][(index * 2) + 1]
					);
					max = max(
						data[channelIndex][pow + 1][index * 2],
						data[channelIndex][pow + 1][(index * 2) + 1]
					);
					rms = (
						data[channelIndex][pow + 1][index * 2].pow(2) + data[channelIndex][pow + 1][(index * 2) + 1].pow(2)
					).sqrt;
					data[channelIndex][pow + 2][index] = [min, max, rms];
				});
			};

			bench {
				if((data[channelIndex][pow + 1].size % 2) == 0) {
					min = min(
						data[channelIndex][pow + 1][data[channelIndex][pow + 1].size - 2],
						data[channelIndex][pow + 1].last
					);
					max = max(
						data[channelIndex][pow + 1][data[channelIndex][pow + 1].size - 2],
						data[channelIndex][pow + 1].last
					);
					rms = (
						data[channelIndex][pow + 1][data[channelIndex][pow + 1].size - 2].pow(2) + data[channelIndex][pow + 1].last.pow(2)
					).sqrt;
					data[channelIndex][pow + 2][data[channelIndex][pow + 2].size - 1] = [min, max, rms];
				} {
					data[channelIndex][pow + 2][data[channelIndex][pow + 2].size - 1] = Array.fill(3, { data[channelIndex][pow + 1].last });
				};
			};
			"".postln;
		});
	});
};

getDRData.value(thisProcess.nowExecutingPath.dirname +/+ "filename.wav");
)

Thanks for your attention,
Simon

2

At a glance, I can’t quite see what’s up, but the algorithm you describe would be ideally implemented as an iterative process.

E.g., if the basic data structure were an array of “min, max, rms,” then you could make one function that takes an array of these triplets and outputs the result of the pairwise reduction (or it could even support other factors). Get this one thing working reliably before proceeding. That’s its only job; don’t embed this into a bigger gnarly process.

Pre-seed the function by converting the channel into an array of triplets (just copy the data 3 times).

Then get the first result – then call the function again on that first result to get the second layer, etc. You can collect these into a bigger data structure if you like, but I suspect one of the issues here is that you’re trying to do it all in a big data structure, making it harder to see what’s happening in the code.

Maybe I could take a stab at it later, but any attempt I make would be to start from scratch.

On my computer, a mono file lasting 300ms takes 45 sec to compute!

That’s definitely a sign of inefficiency – no way that it should take this long to do 9 log2 iterations over < 14000 samples.

hjh

1 Like
3

OK, ended up having some down time. Doing it this way, I get 0.29 seconds to handle a11wlk01.wav – this is ten times longer than your 300 ms case, and 2 orders of magnitude faster = 3 orders of magnitude improvement.

(
~oneDataPoint = { |array, i, n|
	var min = 1e34, max = -1e34, rms = 0;
	n = min(n, array.size - i);
	n.do { |j|
		var row = array[i+j];
		min = min(min, row[0]);
		max = max(max, row[1]);
		rms = rms + row[2].squared;
	};
	[min, max, sqrt(rms / n)]
};

~reduce = { |array, factor = 2|
	var size = (array.size / factor).roundUp.asInteger;
	var new = Array(size);
	size.do { |i|
		new.add(~oneDataPoint.(array, i * factor, factor));
	};
	new
};

~prepArray = { |array|
	array.dup(3).flop
};
)

f = SoundFile.openRead(Platform.resourceDir +/+ "sounds/a11wlk01.wav");
d = Signal.newClear(f.numFrames * f.numChannels);
f.readData(d);
f.close;

(
bench {
	var out;
	a = ~prepArray.(d);
	out = [a];
	while { out.last.size > 1 } {
		out = out.add(~reduce.(out.last, 2));
	};
	o = out
};
)

BTW the higher-level RMS-es will not be true RMS – if you do the RMS calculation over 256 samples, the result is not the same as aggregating previously aggregated results. But for visual display it may be an acceptable approximation.

(Some edits, I kept finding small mistakes in the rms calculation.)

hjh

1 Like
4

Thanks a lot for the help on this!

I’m impressed by the way you are concatenating conditional statements into a single formula. I have to start thinking like this.

This runs, indeed, much faster than what I wrote. Processing a11wlk01 takes 0.8s on my computer, and a 3m30 stereo file took ~70s to compute.

In theory, RMS (which I failed to calculate properly on my code…) should be perfectly deductible from previous iteration right? It’s only rounding errors that accumulates every iteration that are posing problems here?

5

That’s correct – I rechecked my assumptions and found that this is true if all the buckets are the same size (which this algorithm guarantees, except for the last value).

( (a+b)/2 + (c+d)/2 ) / 2 = (a+b+c+d)/4 ok

But, if the chunks have 2 and 3 items respectively, then ( (a+b)/2 + (c+d+e)/3 ) / 2 = (3a+3b+2c+2d+2e)/12, which is not equal to (a+b+c+d+e)/5.

I was thinking of the second case – but you don’t have differently sized buckets in this RMS approach (except at the end), so, no problem.

hjh

1 Like