Bounded Loop / "Power Operator" in SynthDefs?

Questions
1

Do we have a “Power Operator” that works in a SynthDef, somewhat equivalent to ⍣ in APL? For example as in ({1+÷⍵}⍣3)1, applying one function ({1+÷⍵} in this case) n times (3 in this case) to one initial argument?

I don’t remember seeing anything other than n.do{}

4.do({ source = AllpassN.ar(source, 0.050, [Rand(0, 0.05), Rand(0, 0.05)], 1) })

Not the same thing as it is (it would return a function if valid); something along those lines:

{AllpassN.ar(_,0.050,[Rand(0,0.05),Rand(0,0.05)],1)}⍣4

I’ve seen some people playing with operators inside the SD, you guys might know that. (Or even cooler things)

2

I think we don’t.

As an aside, we (SC community) have a love-hate relationship with syntax sugar. Proposals for new syntax sugar are often met with, “oh yeah, that would be cool.” Then, some time down the road, the same syntax sugar may be held up as an example of “why SC is so confusing to learn – too many ways to do the same thing.”

So for me, whether a new syntax sugary thing makes the cut or not depends on how much of a usability improvement the new way is. If the existing way is painful and the new way is significantly easier (and if it’s a frequently-encountered bottleneck), then maybe go for it. If the existing way isn’t that bad and the new way is an incremental improvement (or a side case that doesn’t happen very often), maybe it isn’t necessary.

For me, writing the do loop isn’t so awful. Others’ mileage may vary – so I wouldn’t argue too strenuously against it. (Sure, this thread isn’t a proposal as such, fwiw.)

hjh

1 Like
3

This one is pretty easy to add actually because it is just a left–fold.

This is would be the long version using inject.

( {_ + 4}!n).inject(inital_value, {|acc, f| f.(acc) })

You can then add an operator (or adverb) to Object as a shorthand (I’ll use ⍣ as an example here) , where the right-hand side is expected to be an event with the args in. These args can be validated by the member function.

inital_value ⍣ (n: 10, func: (_ + 4))

You could invert this by extending Function too

(_ + 1) ⍣ (n: 10, init: 2)

Just occasionally, the pure object oriented nature of smalltalk is quite a joy.

Personally, do think that these kinds of operators (piping and the like) should be included because they occur a lot in signal processing.

Here is an implementation for 1 |>.doN (\n: 10, \func: (_ + 0.1))


+Object {
	|> { |f, adverb|
		^case
		{adverb == \doN} {
			if(f.isKindOf(Event).not, {Error("doN requires an Event").throw});
			if(f.size != 2, {Error("doN requires an Event of size 2").throw});
			if(f.includesKey(\n).not, {Error("doN requires an Event with the key 'n' ").throw});
			if(f[\n].isKindOf(Number).not, {Error("doN requires an Event with the key 'n' which is a Number").throw});
			if(f.includesKey(\func).not, {Error("doN requires an Event with the key 'func'").throw});
			if(f[\func].isKindOf(Function).not, {Error("doN requires an Event with the key 'func' which is a Function").throw});

			({f[\func]}.dup(f[\n])).inject( this, {|acc, f| f.(acc) });
        }
   }
}
2 Likes
4

Have a look at miSCellaneous_lib’s GFIS class. I wrote it for implementing Di Scipio’s FIS synthesis, but you can use it also for nested allpass filters. By the way, that hadn’t come to my mind yet, so thanks for the nudge.
In the concrete example there’s no real benefit in terms of typing. However GFIS has some options – e.g. returning different iteration levels – that might be interesting to explore.


// variant with do loop
(
{
	var source = Decay2.ar(Impulse.ar(1)) * Saw.ar(100, 0.1);
	4.do({ source = AllpassN.ar(source, 0.05, [Rand(0, 0.05), Rand(0, 0.05)], 1) });
	source 
}.play
)



// same with GFIS
// different tone colours come from the random components

(
{
	var source = Decay2.ar(Impulse.ar(1)) * Saw.ar(100, 0.1);
	GFIS.ar({ |x| AllpassN.ar(x, 0.05, [Rand(0, 0.05), Rand(0, 0.05)], 1) }, source, 4)
}.play
)




// proof of concept: difference gives silence
// GFIS by default leaks DC (as it was designed with Agostino Di Scipio's FIS synthesis in mind)
// hence turn it off for check

(
{
	var source = Decay2.ar(Impulse.ar(1)) * Saw.ar([100, 150], 0.1);	
	var gfis = GFIS.ar(
		{ |x| AllpassN.ar(x, 0.05, [0.01, 0.011], 1) }, 
		source, 
		4,
		leakDC: false
	);
	4.do({ source = AllpassN.ar(source, 0.05, [0.01, 0.011], 1) });
	source - gfis
}.play
)
1 Like
5

I reckon this particular form of ⍣:

(({⍵*2}⍣3)2)≡256

perhaps written as:

{|x|x**2}.iterate(3,2)==256

is rather useful, particularly in the middle of a sequence of bindings, where one cannot easily write a do loop.

1 Like
6

Maybe this?

+ AbstractFunction {
    iterate { |n, i|
        var r = i;
        n.do { r = this.(r)};
        ^r
    }
}

/*
// (({⍵*2}⍣3)2)≡256

{|x|x**2}.iterate(3,2) == 256
-> true
*/

It could also work with a implementation of a LazyList (I think a quark tried something like this already)

7

I’ll take a look at Di Scipio’s Iterated Nonlinear Functions, it sounds quite interesting. Thank you!

Nested allpass filters are not uncommon. It could be interesting if part of something more general.

FreeVerb, for example:

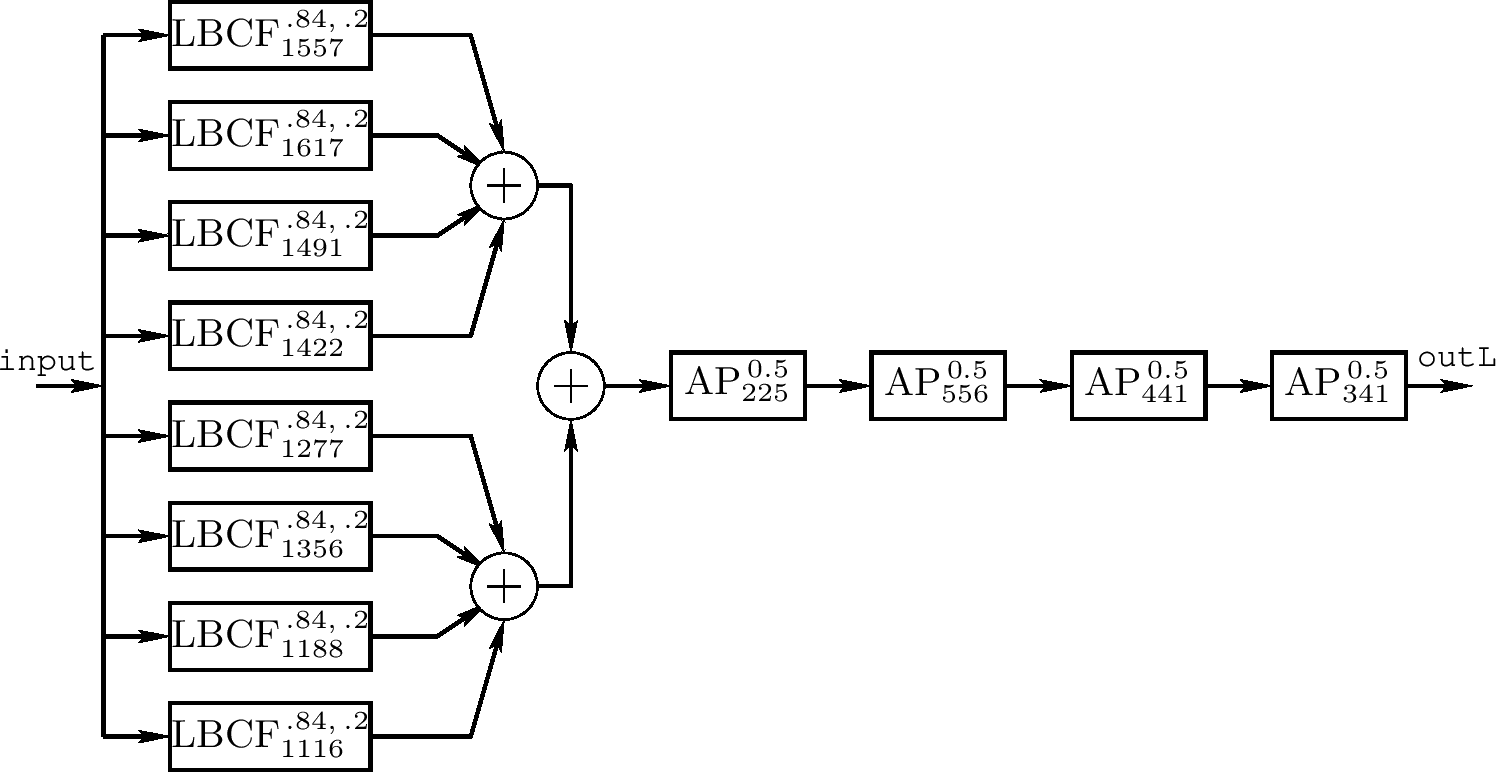
image
image1496×772 17.3 KB

8

Yea, sure.

As you’ve noted, my suggestions do not involve altering the language itself.Given that SuperCollider’s sclang is currently experiencing conservative cycle, it hadn’t even crossed my mind.

I don’t have a love/hate relationship with this historical aspect of sclang. I just appreciate it. That’s how it is.

On a broader note, it’s important to recognize that what might initially seem like ‘syntactic sugar’ can become eventually a qualitative change. When applied extensively in a certain direction, it can be groundwork for new algebraic approach. See APL as a classic example of that. Another example: applications working with circuits use different ideas to represent processes on signals, which might include local loops etc. Those things are not far away from audio signals, and I’m sure they are used elsewhere.

1 Like
9

Sure, and FWIW, I wasn’t saying I would absolutely always oppose introducing a new method.

I think what I was driving at is that we have at times tended to add convenience methods in an ad-hoc way, without a broader plan, and this results in messy interfaces. What you’re talking about in this paragraph is a more organized process, which would be good.

hjh

1 Like
10

Yes, I’m aware of the nested allpass strategies, I just never used GFIS for that.
FWIW, here are some variants derived from the Schroeder ideas:


//////////////////////////
REVERB WITH ALLPASS-FILTER
//////////////////////////



Interesting comment on the 1962 paper by Manfred SCHROEDER from 1962:

https://valhalladsp.com/2009/05/30/schroeder-reverbs-the-forgotten-algorithm/


1.) Comb and Allpass


// Idea: by chosen params a Comb-Delay can be transformed to an Allpass-Delay:


// frequency response with comb delay -> multiples of 500 Hz 500 Hz

s.freqscope;

(
x = {
	var in = WhiteNoise.ar(0.05);
	var delayTime = 0.002; // ~500 Hz
	var decayTime = 0.1;

	var comb = CombL.ar(in, 0.2, delayTime, decayTime);
	comb ! 2;
}.play
)

x.release

// flat frequency response ! (= Allpassfilter)

(
x = {
	var in = WhiteNoise.ar(0.05);
	var delayTime = 0.002; // ~500 Hz
	var decayTime = 0.1;

	var comb = CombL.ar(in, 0.2, delayTime, decayTime);

	// calculate feedback gain
	var fbGain = 0.001 ** (delayTime / decayTime).poll(0, fbGain);

	// mix with correctl chosen params -> flat frequency response
	comb * (1 - (fbGain ** 2)) - (in * fbGain) ! 2;
}.play
)

x.release


// compare with AllpassL -> identical (silence) !

(
x = {
	var in = WhiteNoise.ar(0.05);
	var delayTime = 0.002; // ~500 Hz
	var decayTime = 0.1;

	var comb = CombL.ar(in, 0.2, delayTime, decayTime);

	// calculate feedback gain
	var fbGain = 0.001 ** (delayTime / decayTime).poll(0, fbGain);

	// difference = 0 !
	comb * (1 - (fbGain ** 2)) - (in * fbGain) - AllpassL.ar(in, 0.2, delayTime, decayTime);
}.play
)

x.release


// allpass + source  -> audible frequency (1/delaytime)

(
x = {
	var in = WhiteNoise.ar(0.05);
	var delayTime = 0.002; // ~500 Hz
	var decayTime = 0.1;

	var comb = CombL.ar(in, 0.2, delayTime, decayTime);

	// calculate feedback gain
	var fbGain = 0.001 ** (delayTime / decayTime).poll(0, fbGain);

	// allpass + source
	comb * (1 - (fbGain ** 2)) - (in * fbGain) + in ! 2;

	// identical
	// AllpassL.ar(in, 0.2, delayTime, decayTime) + in ! 2;
}.play
)

x.release

/////////////////////////////////////////////


2.) Schroeder Reverb I: serial allpass  (P.221, 222)

(
s.options.blockSize = 1;
s.reboot;
)


(
// number of allpas filters in sequence
~num = 5;
~fxBus = Bus.audio(s, 2);


// force nicely distributed random numbers for deviation of allpassDelayFactor
// this seed worked ok for me, try others

~minCombDelayTime = 30;
thisThread.randSeed = 121;

~allpassDelayFactorDeviationMax = 0.1;
~allpassDelayFactorDeviations = { rand2(~allpassDelayFactorDeviationMax) } ! ~num + 1;

"~allpassDelayFactorDeviations: ".postln;
~allpassDelayFactorDeviations.do(_.postln);


SynthDef(\schroeder_I, { |outBus, amp = 1, initDelay = 30, cutoff = 7000, overallGain = 0.89|

	var out, in = In.ar(~fxBus, 2);
	var sig = in;
	var maxDelay = 0.2;

	// Schroeder suggestions
	var allpassGain = 0.7;
	var firstAllpassDelay = 30;
	var allpassDelayFactor = 1/3;

	var allpassDelay = firstAllpassDelay * 0.001;
	var fb = LocalIn.ar(2);

	sig = DelayL.ar(fb + sig, 0.2, initDelay * 0.001 - ControlDur.ir);

	{ |i|
		var decay;
		(i != 0).if { allpassDelay = allpassDelay * allpassDelayFactor * ~allpassDelayFactorDeviations[i] };
		decay = allpassDelay * log(0.001) / log(allpassGain);
		sig = AllpassL.ar(sig, maxDelay, allpassDelay, decay);
	} ! ~num;

	// variant: damping of high frequencies
	LocalOut.ar(overallGain * BHiShelf.ar(sig, cutoff, 1, -18));

	out = (1 - (overallGain ** 2)) * sig - (in * overallGain);
	Out.ar(outBus, out * amp)
}, metadata: (
	specs: (
		amp: [0, 1, \db, 0, 0.5],
		initDelay: [2, 1000, 3, 0, 30],  // in ms
		overallGain: [0, 1, \lin, 0, 0.89],
		cutoff: [200, 16000, \exp, 0, 7000]
	)
)
).add;

SynthDef(\sawPerc, { |out, freq = 400, att = 0.01, rel = 0.1, amp = 0.1|
	var env = EnvGen.ar(Env.perc(att, rel), doneAction: 2);
	Out.ar(out, Saw.ar(freq * [1, 1.02], amp) * env)
}).add;
)



// needs miSCellaneous_lib
\schroeder_I.sVarGui.gui(sliderWidth: 320, labelWidth: 120)

// alternative:
SynthDescLib.global[\schroeder_I].makeGui

(
x = Pbind(
	\instrument, \sawPerc,
	\dur, 0.2,
	\note, Prand([0, 2, 4, 7, 9], inf),
	\octave, 4,
	\amp, 0.3,
	\out, ~fxBus
).play
)

x.stop

// stop reverb in GUI

/////////////////////////////////////////////


2.) Schroeder Reverb II: 4 parallele Combs + 2 Allpass in Serie (S. 223)


(
~combNum = 4;
~allpassNum = 2;  // if you change this, you must adapt allpassDelayTimes and allpassGains

~fxBus = Bus.audio(s, 2);

// force nicely distributed random numbers for comb delaytimes
// this seed worked ok for me, try others

thisThread.randSeed = 121;

~combDelayTimeSpread = 1.5;
~combDelayTimeFactors = { |i|
	((~combDelayTimeSpread - 1 * i) + rand(~combDelayTimeSpread - 1)) / ~combNum + 1
} ! ~combNum;


"minCombDelayTime: ".post;
~minCombDelayTime.post;
" ms".postln;
"combDelayTimeFactors: ".postln;
~combDelayTimeFactors.do(_.postln);


SynthDef(\schroeder_II_vs_1, { |outBus, amp = 0.7, mix = 0.12, minCombDelay = 30, revTime = 1|

	var minCombDelayTime = 30;
	var combDelayTimes = ~combDelayTimeFactors * minCombDelay * 0.001;

	// calculate from desired reverb time according to Schroeder
	var combGains = 10 ** (-3 * combDelayTimes / revTime);

	// fix allpass delaytime choices by Schroeder
	var allpassDelayTimes = [5, 1.7] * 0.001;
	var allpassGains = [0.7, 0.7];

	var sig, out;
	var in = In.ar(~fxBus, 2);
	var maxDelay = 0.2;

	var combDecayTimes = combDelayTimes * log(0.001) / log(combGains);
	var allpassDecayTimes = allpassDelayTimes * log(0.001) / log(allpassGains);

	// core:

	// ~combNum parallel Combs for L and R ...
	sig = { |i| CombL.ar(in[i], maxDelay, combDelayTimes, combDecayTimes).sum } ! 2;

	// ... followed by 2 sequential Allpasses
	{ |i| sig = AllpassL.ar(sig, maxDelay, allpassDelayTimes[i], allpassDecayTimes[i]) } ! ~allpassNum;

	out = mix * sig - ((1 - mix) * in);
	Out.ar(outBus, out * amp)
}, metadata: (
	specs: (
		amp: [0, 1, \db, 0, 0.7],
		mix: [0, 1, 3, 0, 0.12],
		minCombDelay: [1, 150, \lin, 0, 30],
		revTime: [0, 15, 3, 0, 1]
	)
)
).add;

SynthDef(\sawPerc, { |out, freq = 400, att = 0.01, rel = 0.1, amp = 0.1|
	var env = EnvGen.ar(Env.perc(att, rel), doneAction: 2);
	Out.ar(out, Saw.ar(freq * [1, 1.02], amp) * env)
}).add;
)

// needs miSCellaneous_lib
\schroeder_II_vs_1.sVarGui.gui(sliderWidth: 320, labelWidth: 120)

// alternative:
SynthDescLib.global[\schroeder_II_vs_1].makeGui


// minCombDelay should be 30 (recommended by S.)
(
x = Pbind(
	\instrument, \sawPerc,
	\dur, 0.2,
	\note, Prand([0, 2, 4, 7, 9], inf),
	\octave, 4,
	\amp, 0.3,
	\out, ~fxBus
).play
)

x.stop

// stop reverb in GUI


(
~combNum = 4;

~fxBus = Bus.audio(s, 2);

// force nicely distributed random numbers for comb delaytimes
// this seed worked ok for me, try others

~minCombDelayTime = 30;
thisThread.randSeed = 121;

~combDelayTimeSpread = 1.5;
~combDelayTimeFactors = { |i|
	((~combDelayTimeSpread - 1 * i) + rand(~combDelayTimeSpread - 1)) / ~combNum + 1
} ! ~combNum;


"minCombDelayTime: ".post;
~minCombDelayTime.post;
" ms".postln;
"combDelayTimeFactors: ".postln;
~combDelayTimeFactors.do(_.postln);


SynthDef(\schroeder_II_vs_2, { |outBus, amp = 0.7, mix = 0.12, revTime = 1, revCorr = 0.5, srcCorr = 0.2, cutoff = 3500|

	var minCombDelayTime = 30;
	var combDelayTimes = ~combDelayTimeFactors * minCombDelayTime * 0.001;

	// calculate from desired reverb time according to Schroeder
	var combGains = 10 ** (-3 * combDelayTimes / revTime);

	// fix allpass delaytime choices by Schroeder
	var allpassDelayTimes = [5, 1.7] * 0.001;
	var allpassGains = [0.7, 0.7];

	var sig, out;
	var in = In.ar(~fxBus, 2);
	var maxDelay = 0.2;

	var combDecayTimes = combDelayTimes * log(0.001) / log(combGains);
	var allpassDecayTimes = allpassDelayTimes * log(0.001) / log(allpassGains);

	// core:

	// dampened input, 4 parallel Combs for L and R  ...
	sig = { |i| CombL.ar(BHiShelf.ar(in[i], cutoff, 1, -18), maxDelay, combDelayTimes, combDecayTimes).sum } ! 2;

	// ... followed by 2 sequential Allpasses
	{ |i| sig = AllpassL.ar(sig, maxDelay, allpassDelayTimes[i], allpassDecayTimes[i]) } ! ~allpassNum;

	// correlations for src and reverb
	in = [
		XFade2.ar(in[0], in[1], srcCorr - 1),
		XFade2.ar(in[0], in[1], 1 - srcCorr)
	];
	// better: SelectX.ar(srcCorr, [in, in.sum ! 2])
	sig = [
		XFade2.ar(sig[0], sig[1], revCorr - 1),
		XFade2.ar(sig[0], sig[1], 1 - revCorr)
	];
	// better: SelectX.ar(revCorr, [sig, sig.sum ! 2])

	out = mix * sig - ((1 - mix) * in);
	Out.ar(outBus, out * amp)
}, metadata: (
	specs: (
		amp: [0, 1, \db, 0, 0.7],
		mix: [0, 1, 3, 0, 0.12],
		revTime: [0, 15, 3, 0, 1],
		revCorr: [0, 1, \lin, 0, 0.5],
		srcCorr: [0, 1, \lin, 0, 0.2],
		cutoff: [200, 16000, \exp, 0, 3500]
	)
)
).add;

SynthDef(\sawPerc_2, { |out, freq = 400, att = 0.01, rel = 0.1, pan = 0, amp = 0.1|
	var env = EnvGen.ar(Env.perc(att, rel), doneAction: 2);
	Out.ar(out, Pan2.ar(Saw.ar(freq, amp), pan) * env)
}).add
)

// needs miSCellaneous_lib
\schroeder_II_vs_2.sVarGui.gui(sliderWidth: 320, labelWidth: 120)

// alternative:
SynthDescLib.global[\schroeder_II_vs_2].makeGui


(
x = Pbind(
	\instrument, \sawPerc_2,
	\dur, 0.2,
	\note, Prand([0, 2, 4, 7, 9], inf) + [0, 16],
	\octave, 4,
	\pan, [-1, 1],
	\amp, 0.3,
	\out, ~fxBus
).play
)

x.stop

// stop reverb in GUI
1 Like
11

Yes, a stream form is nice too, perhaps as below?

Which suggests placing the count second, so the “switch on nil” idiom works nicely:

{ |x| x ** 2 }.iterate(2, 3) == 256
{ |x| x ** 2 }.iterate(2).nextN(4) == [2, 4, 16, 256]

Functon>>iterate:

	iterate { |anObject|
		var state = anObject;
		^FuncStream {
			var next = state;
			state = this.value(state);
			next
		} {
			state = anObject
		}
	}

Ps. You don’t need the var r above, you’re allowed to mutate i!

1 Like
12

Rohan @rdd , all of these implementations are very idiomatic, and fit perfectly into the sclang style.

I like them.

I know. It just didn’t feel right to mutate an argument named “initial”, or start with an argument named “result” as the initial value. That was just a naming thing here.

EDIT, OT: I was trying out your hsc3 project, and it seems you’re reworking the syntax for some things. Is it under revision right now?

13

Thanks for the reply, quite cool.

Actually it could be also an unfoldr, couldn’t it? Foldr reduces a list to a value, while unfoldr builds a list from a seed value. If you want to have the intermediate signals/number/values too.

unfoldr (\x -> if x == 0 then Nothing else Just (x, x-1)) 10
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]

OR:

iterate :: (a -> a) -> a -> [a]
iterate f x =  x : iterate f (f x)

Something too would be a replicate, a map, and a reduce.

14

Something useful too would be a replicate, a map, and a reduce.

I’m sure you know this already, but replicate is !, map is collect, foldl1 is reduce?

Ie.

1!5 == [1,1,1,1,1]
[1,2,3].collect(_+1) == [2,3,4]
[1,2,3].reduce(_-_) == -4

Cf.

replicate 5 1 == [1,1,1,1,1]
map (+ 1) [1,2,3] == [2,3,4]
foldl1 (-) [1,2,3] == -4

But in any case, the first part of the diagram above would, in Sc, just be:

LBCF.ar(input, 0.84, 0.2, [1557, 1617, 1491, 1422, &etc.]).sum

Ps. I don’t think there’s been much change at hsc3? Write me off list if anything isn’t working?

1 Like
15

Yes, of course. I was thinking as one operation. All that is simple programming, I’m just wondering about a simple “mapreduce” pattern, no claims of novelty no far))))

Going a bit further with the “mapReduce” idea, map can process in more different ways, or even analyzing. There could be a shuffle intermediate data, and reduce could also do a bit more, like adjusting levels or applying crossfades etc. Theoretically those kind of things could be done in parallel, but that’s not the case inside a SD>