On current stability issues in BPF. Feedback, concerns, or suggestions are welcome.
The current implementation has some issues with negative frequencies and instabilities near zero. The BPF calculates its coefficients using the standard tangent function:
double pfreq = freq * unit->mRate->mRadiansPerSample;
double pbw = bw * pfreq * 0.5;
double C = 1 / tan(pbw);
The distortions occur because:
- Negative pfreq results in negative pbw.
- Tangent of negative values or near zero can produce very large negative numbers.
- Dividing 1 by these large numbers leads to very small values or floating-point instabilities.
- These abnormal values propagate through subsequent calculations, resulting in filter coefficients outside normal ranges.
The result can be distortions, loud pops, clicks, or extremely (dangerous) loud output.
Possible change: Chebyshev Polynomial Approximation
One possible enhancement could be to replace the tangent calculation with a Chebyshev approximation. For example:
constexpr double PI_4 = 0.7853981633974483;
constexpr double c1 = 1.3800431431142994;
constexpr double c3 = 0.1546028061638477;
constexpr double c5 = 1.9821882628706124e-2;
constexpr double c7 = 2.5538677244514307e-3;
constexpr double c9 = 2.879200910730129e-4;
double chebyshev_tan_approx(double x) {
// Range reduction, if necessary
// function is most accurate for x in -π/4 ~ π/4
int quadrant = std::round(x / PI_4);
x -= quadrant * PI_4;
double x2 = x * x;
double x4 = x2 * x2;
double p = (c5 + x2 * c7) + x4 * c9;
double result = x * (c1 + x2 * (c3 + x2 * p));
return (quadrant & 1) ? (1.0 / result) : result;
}
double C = 1.0 / chebyshev_tan_approx(pbw);
why?
-
Avoids instabilities near zero and with negative frequencies.
-
Potentially 2-5 times faster on average.
-
The filter’s accuracy will depend on the accuracy of the Chebyshev approximation. We may need to adjust the number of terms in the polynomial.
-
Chebyshev approximation relies on basic arithmetic operations, which are far less computationally intensive than transcendental calculations.
Reference
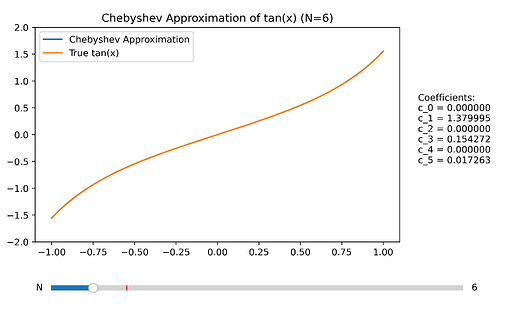
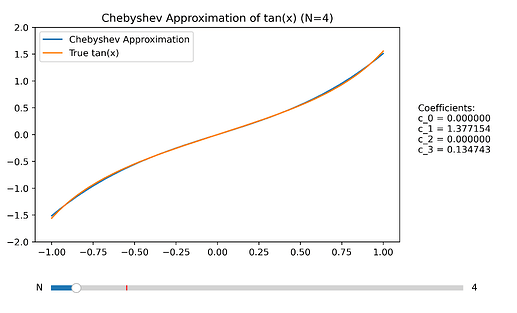
This Python code directly implements this formula. It calculates the coefficients to the N degree of approximation.
import math
def chebyshev_tan_coeffs(N):
coeffs = [0.0] * N
PI = math.pi
for j in range(N):
sum = 0.0
for k in range(1, N + 1):
x_k = math.cos(PI * (k - 0.5) / N)
sum += math.tan(x_k) * math.cos(j * math.acos(x_k))
coeffs[j] = (2.0 / N) * sum
return coeffs
Testing this methodś precision: 6 is a very good approximation. Anything less than 5 or 4 is imprecise. The C++ code above uses N=10 (see output below), maybe unecessary.
Comparison implemented in Haskell. The results show that the approximation is very accurate, with differences typically in the order of 10^-5 or smaller:
import Data.List (genericLength)
import Text.Printf (printf)
chebyshevTanCoeffs :: Int -> [Double]
chebyshevTanCoeffs n =
let n' = fromIntegral n
pi' = pi :: Double
coeffs = [sum [tan (x_k k) * cos (fromIntegral j * acos (x_k k)) | k <- [1..n]] | j <- [0..n-1]]
x_k k = cos (pi' * (fromIntegral k - 0.5) / n')
in map ((2.0 / n') *) coeffs
chebyshevTanApprox :: [Double] -> Double -> Double
chebyshevTanApprox coeffs x =
let n = length coeffs
result = (head coeffs) / 2 + sum [coeffs !! i * cos (fromIntegral i * acos x) | i <- [1..n-1]]
in result
-- chebyshevTanCoeffs 10
--[8.881784197001253e-17,1.3800431431142994,3.1086244689504386e-16,0.1546028061638477,7.105427357601002e-16,1.9821882628706124e-2,1.1546319456101628e-15,2.5538677244514307e-3,1.7097434579227411e-15,2.879200910730129e-4
compareTanApprox :: Int -> IO ()
compareTanApprox n = do
let coeffs = chebyshevTanCoeffs n
putStrLn $ "Coefficients for N = " ++ show n ++ ":"
mapM_ (\(i, c) -> printf "c_%d = %.15e\n" i c) $ zip [0..] coeffs
putStrLn "\nComparison of approximation vs actual tan:"
let testPoints = [0.1, 0.2 .. 0.9]
let results = map (\x -> (x, chebyshevTanApprox coeffs x, tan x)) testPoints
mapM_ (\(x, approx, actual) ->
printf "x = %.2f: Approx = %.6f, Actual = %.6f, Diff = %.6e\n"
x approx actual (abs (approx - actual))
) results
main :: IO ()
main = do
putStrLn "Enter the degree of approximation (N):"
n <- readLn
compareTanApprox n
-->main
--Enter the degree of approximation (N):
--10
--Coefficients for N = 10:
--c_0 = 8.881784197001253e-17
--c_1 = 1.380043143114299e0
--c_2 = 3.108624468950439e-16
--c_3 = 1.546028061638477e-1
--c_4 = 7.105427357601002e-16
--c_5 = 1.982188262870612e-2
--c_6 = 1.154631945610163e-15
--c_7 = 2.553867724451431e-3
--c_8 = 1.709743457922741e-15
--c_9 = 2.879200910730129e-4
--
--Comparison of approximation vs actual tan:
--x = 0.10: Approx = 0.100338, Actual = 0.100335, Diff = 3.156938e-6
--x = 0.20: Approx = 0.202705, Actual = 0.202710, Diff = 5.081993e-6
--x = 0.30: Approx = 0.309318, Actual = 0.309336, Diff = 1.808463e-5
--x = 0.40: Approx = 0.422779, Actual = 0.422793, Diff = 1.403397e-5
--x = 0.50: Approx = 0.546319, Actual = 0.546302, Diff = 1.623064e-5
--x = 0.60: Approx = 0.684177, Actual = 0.684137, Diff = 4.051529e-5
--x = 0.70: Approx = 0.842293, Actual = 0.842288, Diff = 5.088008e-6
--x = 0.80: Approx = 1.029576, Actual = 1.029639, Diff = 6.229755e-5
--x = 0.90: Approx = 1.260174, Actual = 1.260158, Diff = 1.569295e-5
``