Coding FM Synthesis Algorithms

Questions
1

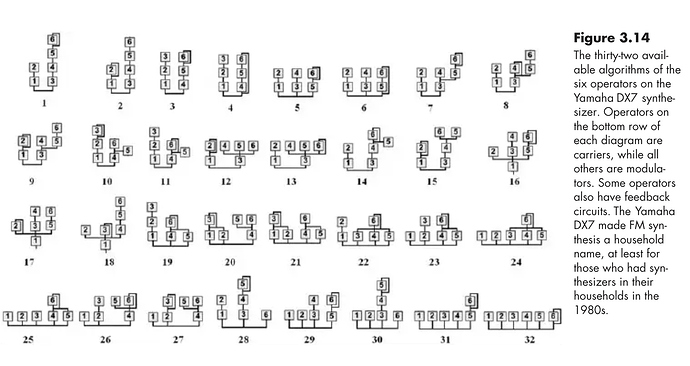
Building off of Eli Fieldsteel’s FM Synthesis synth, I think it would be useful for the community to code other typical FM Synthesis Algorithms, as seen in the DX7. I’d appreciate any help on this. I’ll attach a pic of the diagrams for the algorithms. And I’ll attach the code for the synthdef of Eli’s FM Synth from his tutorials.

55%20PM
Screen Shot 2019-10-20 at 3.28.55 PM.jpg1682×894 231 KB 

//interval space of sidebands = frequency of modulator

//number of audible sidebands = index of modulation = amplitude of modulator

//modulator frequency + carrier frequency = ratio (e.g. 2:1 = 500hz:250hz), then we get harmonic content

//as integers increase for carrier ratio, we get more harmonic sidebands centered on the overtone series, and intervalic spacing stays the same

//non-integers (e.g. 2.1, 2.3, 2.5) for carrier ratio produce inharmonic content that sounds like a bell

//integers used for the modulator ratio, the carrier stays put but the spacing of the sidebands increases, so we get different combinations of specific overtones

//non-integers for modulator ratio produce inharmonic content

//index = modAmp/modHz, loosely corresponds to number of audible sideband pairs in the spectrum



(
SynthDef(\fm, {
	arg freq = 500, mRatio = 1, cRatio = 1, index = 1, iScale = 5, amp = 0.2, atk = 0.01, rel = 3, cAtk = 4, cRel = (-4), pan = 0;
	var car, mod, env, iEnv;
	iEnv = EnvGen.kr(
		Env.new(
			[index, index * iScale, index],
			[atk, rel],
			[cAtk, cRel]
		)
	);
	env = EnvGen.kr(
		Env.perc(atk, rel, curve: [cAtk, cRel]),
		doneAction: 2
	);
	mod = SinOsc.ar(freq * mRatio, mul: freq * mRatio * iEnv);
	car = SinOsc.ar(freq * cRatio + mod) * env * amp;
	car = Pan2.ar(car, pan);
	Out.ar(0, car);
}).add;
)

Synth(\fm, [\freq, 46.midicps, \rel, 1, \index, 20, \iScale, 0.10, \mRatio, 2.0]);


(
Pbind(
	\instrument, \fm,
	\freq, Pseq([73.42, 87.31, 130.81, 146.83, 98, 116.54, 174.61, 233.08, 73.42, 87.31, 130.81, 146.83, 98, 116.54, 233.08, 174.61], inf),
	\dur, 1/8,
	\stretch, 3.5,
	\mRatio, 1,
	\cRatio, 1,
	\index, 1,
	\iScale, 5,
	\amp, 0.2,
	\atk, 0.01,
	\rel, 3,
	\cAtk, 4,
	\cRel, (-4),
	\pan, 0,
).play;
)
2

In case it can be useful to you, someone made an accurate simulation of a DX7 in supercollider:

3

I would suggest phase modulation instead of FM.

	mod = SinOsc.ar(freq * mRatio, mul: iEnv);
	car = SinOsc.ar(freq * cRatio, mod.wrap(0, 4pi)) * env * amp;

There should be no audible difference for mod -> carrier. (I had to scratch my head over that a while back, but: frequency is the derivative of phase. PM adds a sinusoid to the linearly-increasing phase. The derivative of the linear increase is a flat frequency – check – and the derivative of the sinusoidal modulator is itself a sinusoid – d/dx sin(x) = cos(x) – so phase + sin(…) and freq + cos(…) do the same thing! Simple phase modulation is mathematically equivalent to FM, just with a phase shift in the modulator that you won’t hear.)

For mod2 -> mod1 -> carrier, the frequency will drift away from center with FM, but not with PM.

mod2 -> mod1 is very likely to produce a signal with a strong DC offset. In FM, “-> car” will add this to frequency, so the average frequency applied to the carrier is biased away from true. If you add this to phase instead, then the resulting signal might have a little phase shift but the phasor representing the desired frequency continues at its own rate and you hear the frequency you wanted.

hjh

4

Maybe not an as accurate DX7 model as the one @shiihs suggests , but have you checked the FM7 UGen? Provides an FM7.ar(ctls, mods) and FM7.arAlgo(algo, ctls) methods.

5

Yeah the DX7 code uses the FM7 UGen, it can do any of the classic DX7 algorithms.