I’m working on a wavefolding effect, and I want to have the potential for pre- and post- effect for amplitude modulation or ring mod.
I’ve got an input, along with a pre-gain and post-gain. The modulation is optional, but since it is a multiplication with the signal, I need to be careful about nulling out the main signal.
Currently, I’ve been doing something like this, in pseudo-code:
in = \in.ar([0, 0]);
mod = \mod.ar([0, 0]);
modPreGain = \modPreGain.kr(0);
modPostGain = \modPostGain.kr(0);
modPre = mod * modPreGain;
modPre = modPre + (modPreGain |==| 0);
modPost = mod * modPostGain;
modPost = modPost + (modPostGain |==| 0);
sig = in * modPre;
sig = { effect core here }
sig = sig * modPost;
This works fine at the moment, but I’m wondering if there’s a better way to achieve this type of thing. I’ve thought about Select or ‘.blend’ but if I want control of the gain, then that requires an additional parameter control for pre- and post-.
Thanks,
Boris
Hm, the way you wrote it here, there would be a large discontinuity between e.g. modPreGain = 0.0001 and modPreGain = 0.
Another way to think of it: a dry-wet mix. modPreGain = 0 would correspond to a fully dry signal (no RM), = 1 would be fully wet (100% RM signal), and every mixture in between.
// not modPreGain, but modPreAmt
sig = LinXFade2.ar(sig, sig * mod, modPreAmt * 2 - 1);
Algebraically, this works around to a modulator with an interesting property (which also, when you see it, makes intuitive sense).
// mix = 0 .. 1
linxfade = (b - a) * mix + a
= ((sig * mod) - sig) * mix + sig
= (sig * mod * mix) - (sig * mix) + sig
// here, factoring out sig means
// it's worked back around to ring modulation!
= sig * ((mod * mix) - mix + 1)
// ... i.e., mod has now mul = mix, and add = 1 - mix
// let's plot the final modulator signal then
{
var mix = Line.ar(0, 1, 0.01);
SinOsc.ar(1000) * mix + (1 - mix)
}.plot;
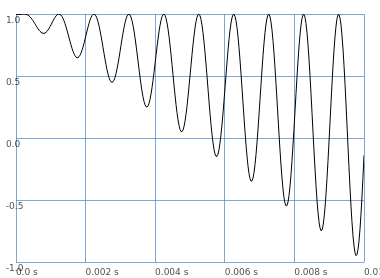
So the LinXFade2 is the same as scaling the modulator (analogous to gain) while also offsetting it so that the peak is always 1.0 (= no nulling-out).
hjh
1 Like
Would there be a discontinuity? If modPreGain = 0.0001, mod would oscillate between 0.0001 and -0.0001, and then, since modPreGain is not equal to 0, the boolean expression would add 0 to the signal.
eg:
modPreGain = 0.0001;
modPre = mod * modPreGain; // oscillates between +/- 0.0001
modPre = modPre + (modPreGain |==| 0); // since modPreGain != 0, this would be the signal from line above + 0.
For example:
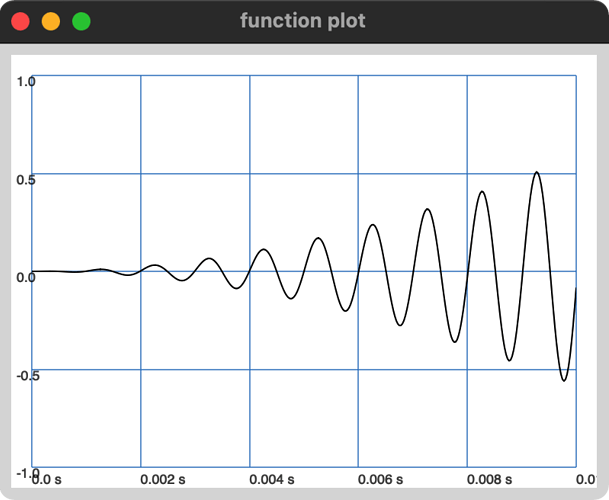
{
var sig = SinOsc.ar(1000);
var modPreGain = Line.ar(0, 1, 0.01);
var mod = 1;
var modPre = mod * modPreGain;
modPre = modPre + (modPreGain |==| 0);
sig * modPre;
}.plot;
)
Or
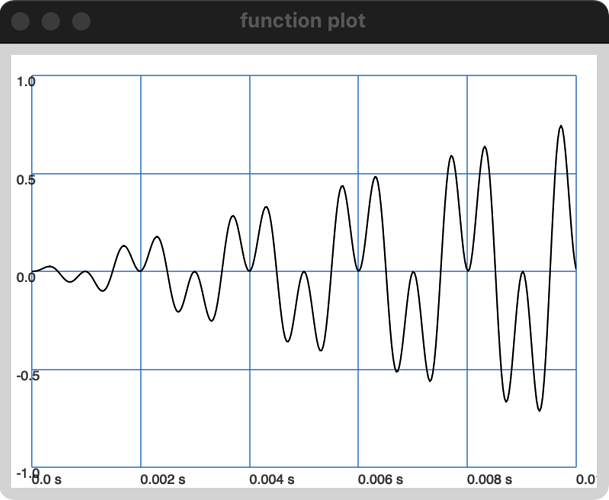
(
{
var sig = SinOsc.ar(1000);
var modPreGain = Line.ar(0, 1, 0.01);
var mod = SinOsc.ar(500);
var modPre = mod * modPreGain;
modPre = modPre + (modPreGain |==| 0);
sig * modPre;
}.plot;
)
The thing I lose by using the dry/wet blending is the ability to either overdrive the signal to taste or to use a negative gain value to flip the phase. The phase flipping especially is interesting to me in my current use case… flipping post- but not pre-, for example.
Oh, I see, the discontinuity may be from no AM or ring mod to a tiny bit:
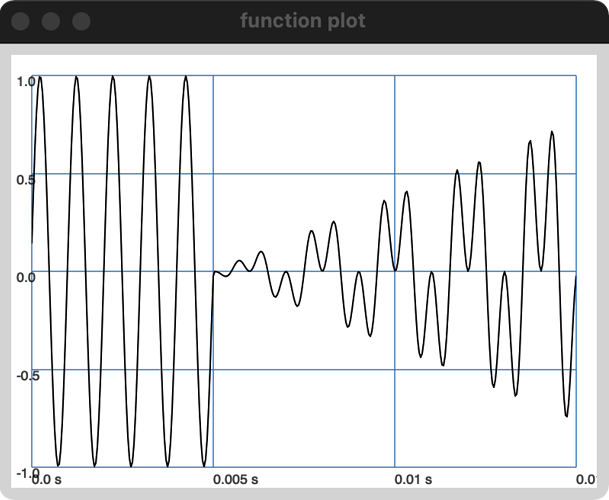
(
{
var sig = SinOsc.ar(1000);
var modPreGain = Env([0, 0, 1], [0.005, 0.01]).ar;
var mod = SinOsc.ar(500);
var modPre = mod * modPreGain;
modPre = modPre + (modPreGain |==| 0);
sig * modPre;
}.plot(0.015);
)
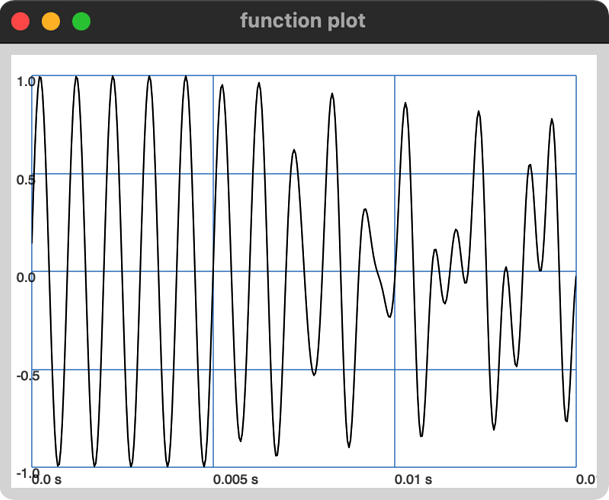
(
{
var sig = SinOsc.ar(1000);
var modPreAmt = Env([0, 0, 1], [0.005, 0.01]).ar;
var mod = SinOsc.ar(500);
sig = LinXFade2.ar(sig, sig * mod, modPreAmt * 2 - 1);
}.plot(0.015);
)
Hm, then:
// -1 <= modGain <= 1
sig = sig * ((mod * modGain) + (1 - abs(modGain)))
(
a = {
var modGain = Line.ar(-1, 1, 0.02);
var positiveGain = modGain.fold(0, 1);
// plot modulator only
var mod = SinOsc.ar(1000);
[
// upper: no negative gain allowed
((mod * positiveGain) + (1 - positiveGain)),
// lower: with negative gain
((mod * modGain) + (1 - abs(modGain)))
]
}.plot(duration: 0.02);
)
hjh
1 Like
Thanks! This is working nicely!