I implemented a spline to replace sharp corners in functions. Suppose we have the following function:
(
f = { |x|
var out;
out = if(x <= 0,
x.lincurve(-1, 0, -1, 0, 5),
x
);
out = if(x > 0,
x.lincurve(0, 1, 0, 1, 5),
out
);
out
};
{ |x| f.(x) }.plotGraph(500, -1, 1)
)
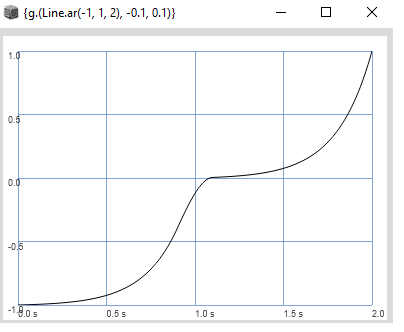
This shows the following plot:
There is a sharp corner for x = 0. I wanted this to be smoothed out. So i used cubic splining for this. I do this by choosing an interval which has the sharp corner in it. So in this case the sharp corner is on x = 0, so i choose the interval [-0.1, 0.1]:
(
g = { |x, startSpline, endSpline|
var out, spline;
spline = CubicSpline.new(f).spline(startSpline, endSpline);
out = if(x <= 0,
f.(x),
x
);
out = if(x > 0,
f.(x),
out
);
out = if(x >= startSpline && (x <= endSpline),
spline.(x),
out
);
};
{ |x| g.(x, -0.1, 0.1) }.plotGraph(500, -1, 1)
)
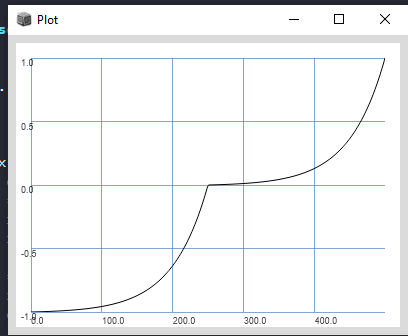
This shows the following plot:
So it does seem to work. But i also want it to work for uGens.
When i adjust the code a little bit and use a phasor to represent a straight line from -1 to 1, it doesnt seem to work anymore:
(
g = { |x, startSpline, endSpline|
var out, spline;
spline = CubicSpline.new(f).spline(startSpline, endSpline);
out = if(x <= 0,
f.(x),
x
);
out = if(x > 0,
f.(x),
out
);
//the mentioned adjustment is && --> &
out = if(x >= startSpline & (x <= endSpline),
spline.(x),
out
);
};
{g.(Phasor.ar(DC.ar(0), 44100.reciprocal, -1, 1), -0.1, 0.1)}.plot(2)
)
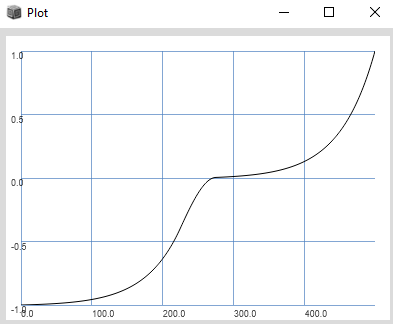
This shows the following plot:
Does anyone have an indication of what might be the problem? Any tips for finding the problem?
Here is the cubicspline class:
CubicSpline {
//this is the function that needs to be splined
var func;
*new { | function |
^super.newCopyArgs(function);
}
//calculates the slope for a certain x
calcSlope { |x|
^[func.(x + (1e-13)) - func.(x) / (1e-13)]
}
//calculates the y coordinate for a certain x
calcY { |x|
^[func.(x)]
}
//calculates a matrix row based on func
calcRow { |x|
^[x**3, x**2, x, 1]
}
//calculates a matrix row based on the derivative of func
calcRowDeriv { |x|
^[3*(x**2), 2*x, 1, 0]
}
//now a bunch of functions with arguments x1 and x2 will show up
//x1 and x2 are the x-coordinates of the starting and endpoint respectively
//we want to calculate X = A^(-1) * B
//X, A and B are matrices and A^(-1) is the inverse of A
calcMatrixA { |x1, x2|
var row0, row1, row2, row3;
row0 = this.calcRow(x1);
row1 = this.calcRow(x2);
row2 = this.calcRowDeriv(x1);
row3 = this.calcRowDeriv(x2);
^[row0, row1, row2, row3]
}
calcMatrixB { |x1, x2|
var row0, row1, row2, row3;
row0 = this.calcY(x1);
row1 = this.calcY(x2);
row2 = this.calcSlope(x1);
row3 = this.calcSlope(x2);
^[row0, row1, row2, row3]
}
//calculate the inverse of a matrix
calcInverse { |x1, x2|
//here i used the matrix class from mathlib
^Matrix.with(this.calcMatrixA(x1, x2)).inverse.asArray;
}
//calculate the multiplication of two matrices
calcMul { |x1, x2|
^MyMatrix.mul(this.calcInverse(x1, x2), this.calcMatrixB(x1, x2))
}
//return the spline, based on a starting and an end point
spline { |x1, x2|
var a, b, c, d;
var matrix = this.calcMul(x1, x2);
a = matrix[0][0];
b = matrix[1][0];
c = matrix[2][0];
d = matrix[3][0];
^{ |x| a*(x**3) + (b * (x**2)) + (c * x) + d }
}
}
I use a matrix multiplication method from my own defined class MyMatrix, since Matrix.mul from mathlib doesnt work well fully. Here is that class:
MyMatrix{
*mul{|m1, m2|
var result = 0;
if(m1[0].size == m2.size,
{result = MyMatrix.calcmul(m1, m2)},
{"not compatible matrices".postln}
);
^result
}
*calcmul{|m1, m2|
var result = Array.fill(m1.size, {Array.fill(m2[0].size, {0})});
var flippedm2 = MyMatrix.flip(m2);
result.do{|x, i|
result[i].do{|y, j|
result[i][j] = (m1[i]*flippedm2[j]).sum;
}
};
^result
}
*flip{|m|
var result = Array.fill(m[0].size, {Array.fill(m.size, {0})});
result.do{|x, i|
result[i].do{|y, j|
result[i][j] = m[j][i]
}
};
^result
}
*calcInverse { |m|
//still to be implemented
}
}