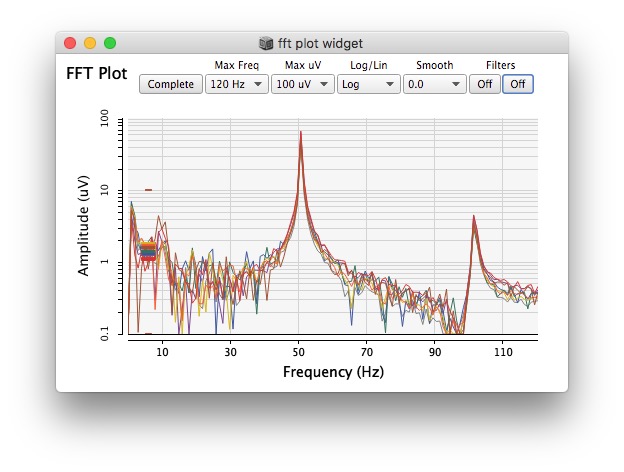
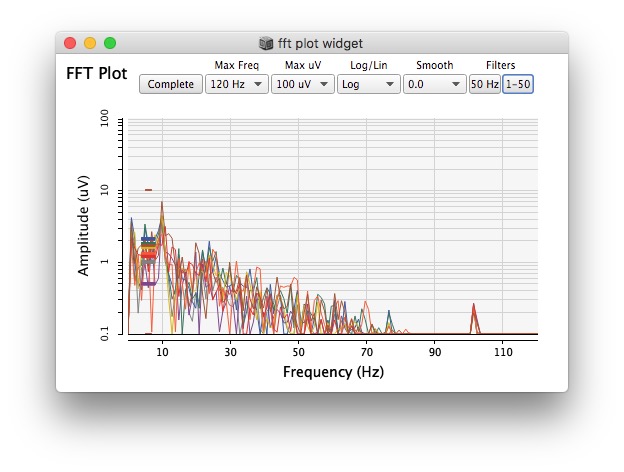
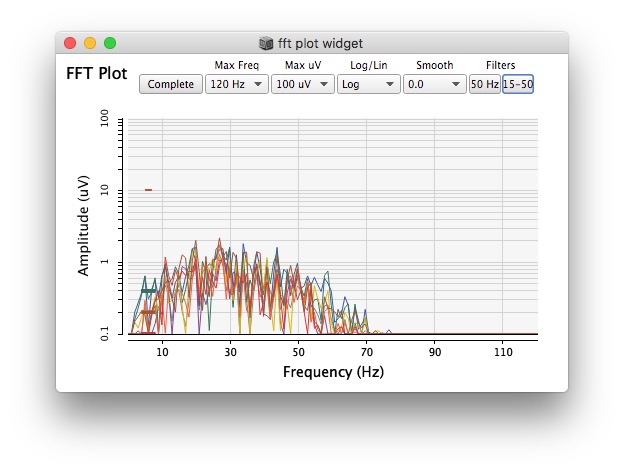
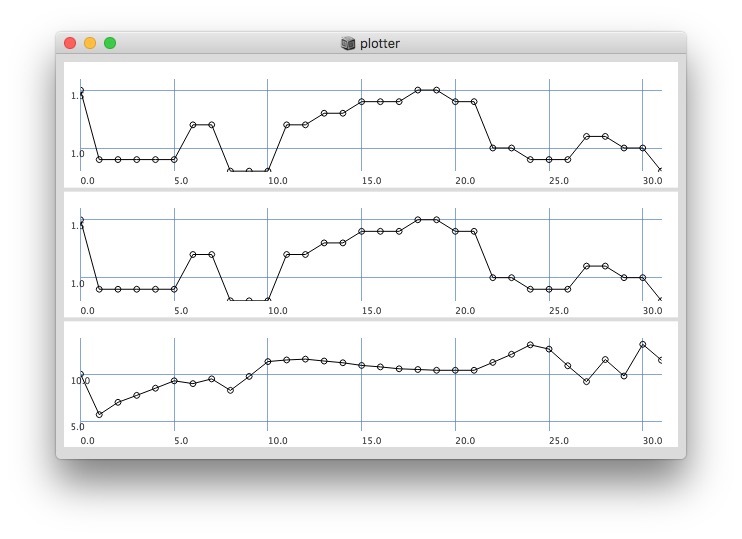
many thanks, I changed to code:
(
var tempX= nil;
var tempY= nil;
x= Signal.newClear(512).fill(0); //change size to 512 for longer window
y= Signal.newClear(512).fill(0); //change size to 512
a= Signal.newClear(512).fill(0); //change size to 512
c= Signal.newClear(512).fill(0); //change size to 512
r= Routine.run({inf.do{
x= x.rotate(-1).postln;
y= y.rotate(-1).postln;
a= a.rotate(-1);
c= c.rotate(-1);
x[x.size-1]= ~bandEnergyAvg[6];
y[y.size-1]= ~bandEnergyAvg[6]; //change
// throw away DC (irrelevant to phase)
tempX = x - x.mean;
tempY = y - y.mean;
// normalize after DC removal
// hope you don't have any all-0 data sets
tempX = tempX / tempX.abs.maxItem;
tempY = tempY / tempY.abs.maxItem;
// now I'm not sure if you need to divide here
// because data ranges have already been controlled
b= sum(tempX * tempY) /* /sum(tempX.squared) */;
b= sum(x*y)/sum(x.squared);
a[a.size-1]= b;
a.postln;
(1/25).wait;
}});
);
r.stop;
(
var data = [x,y,a];
var plotter = Plotter("plotter",Rect(5,5,630,405));
plotter.plotMode = \plines;
plotter.value_(data);
);
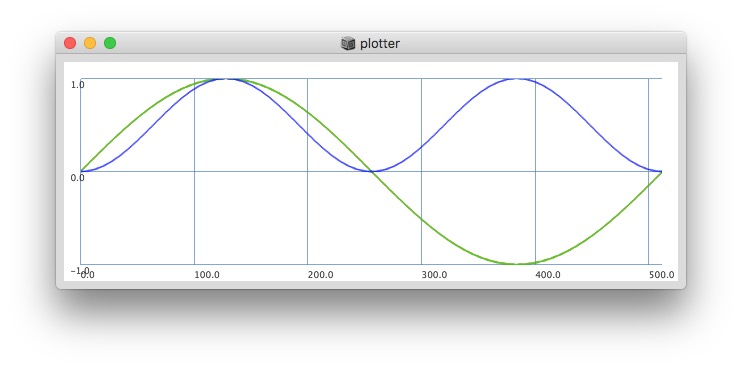
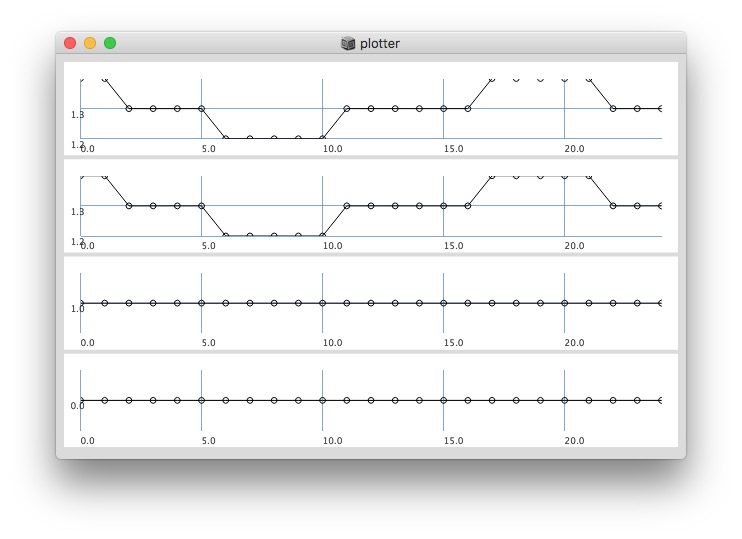
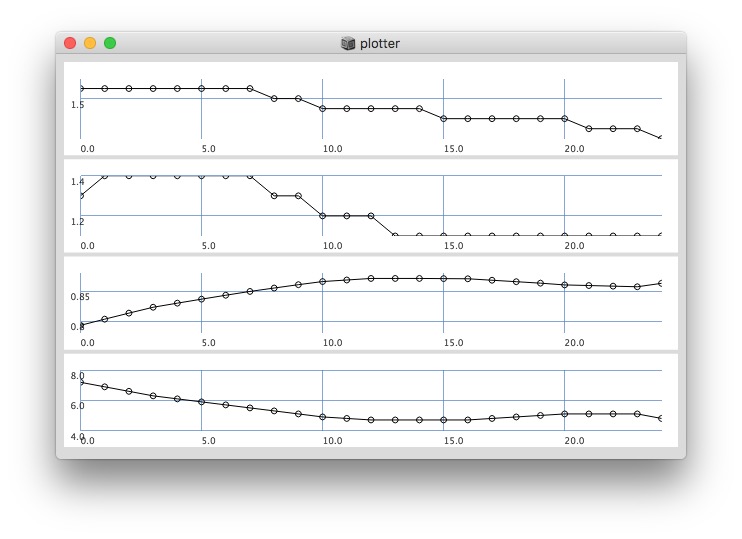
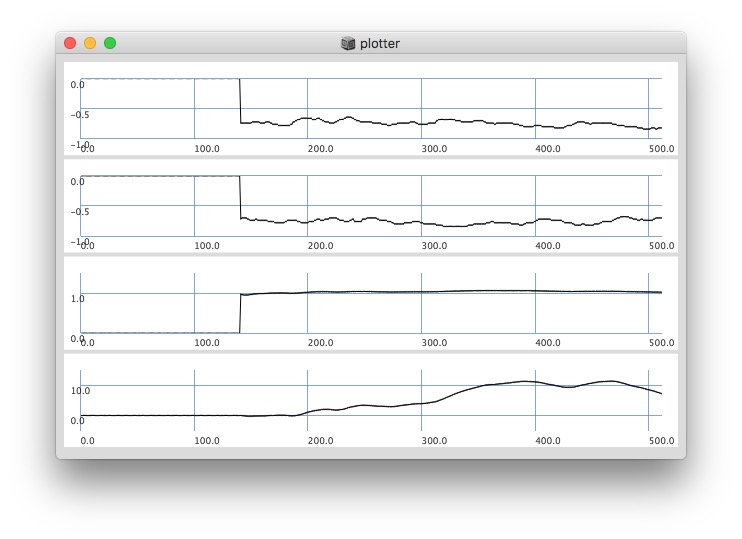
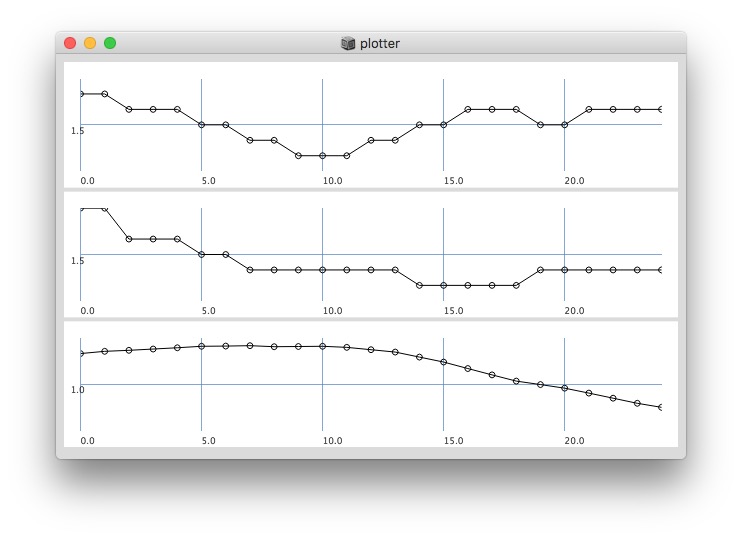
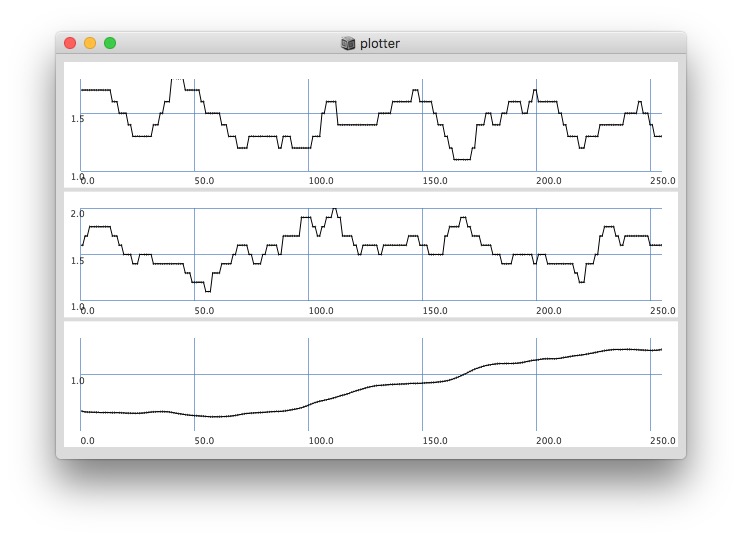
Plotting same signal (~bandEnergyAvg[6]) with 25 and 512 sized window:
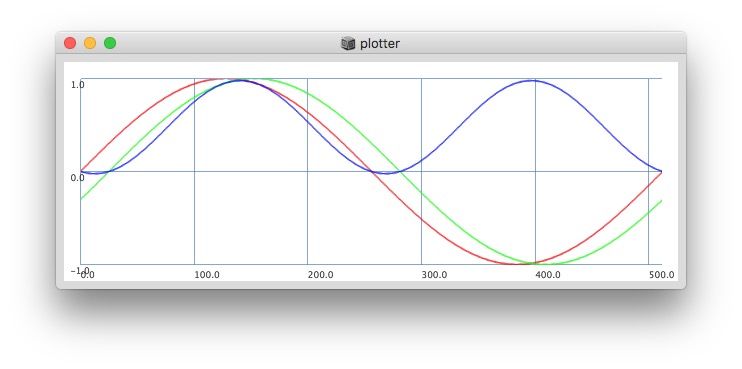
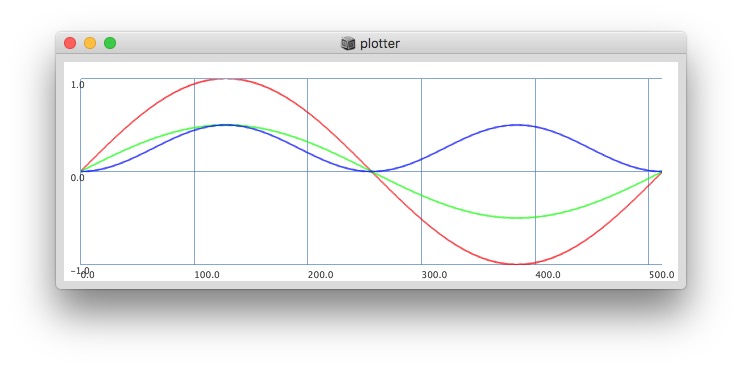
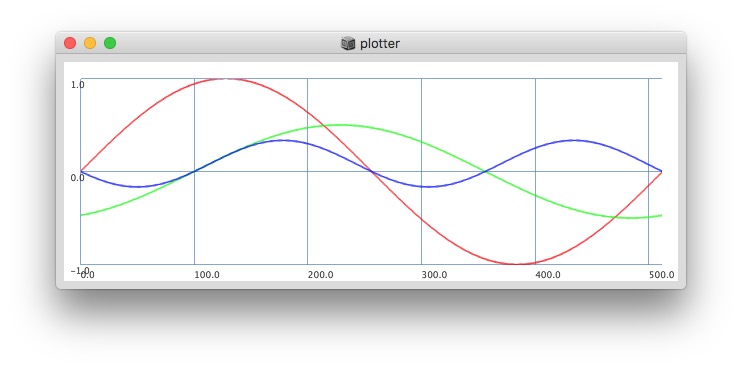
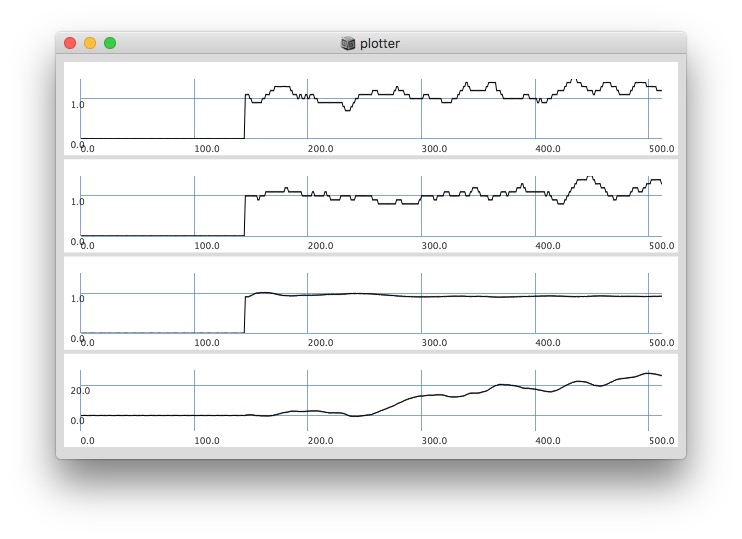
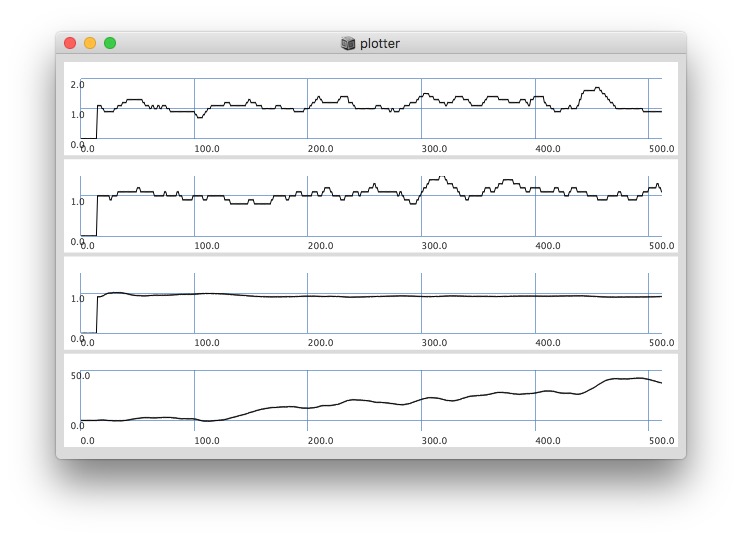
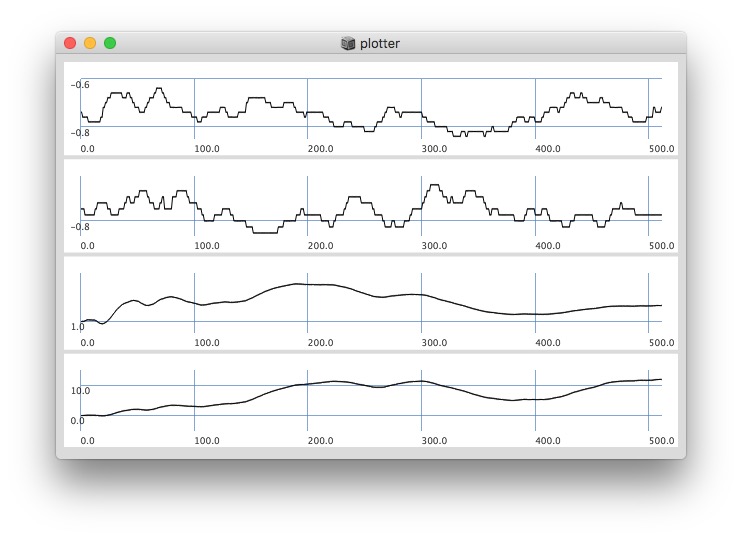
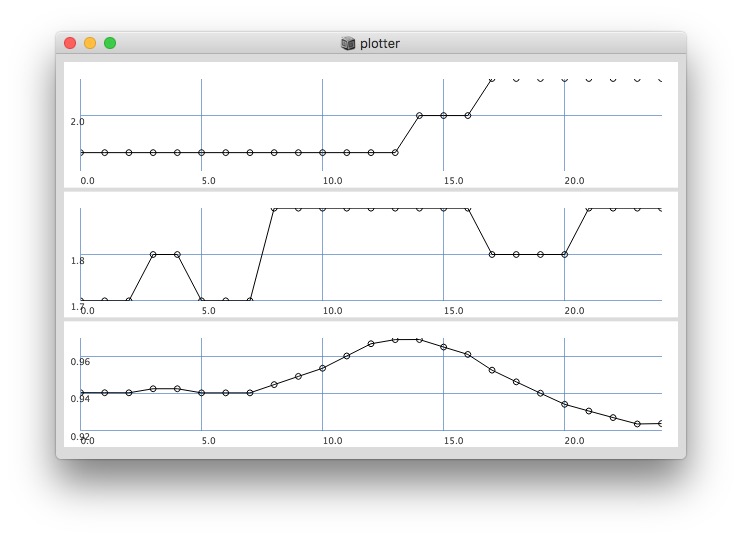
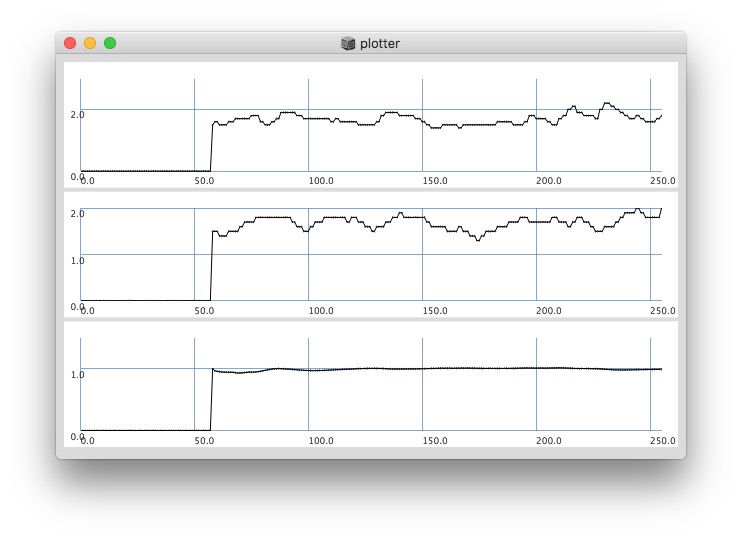
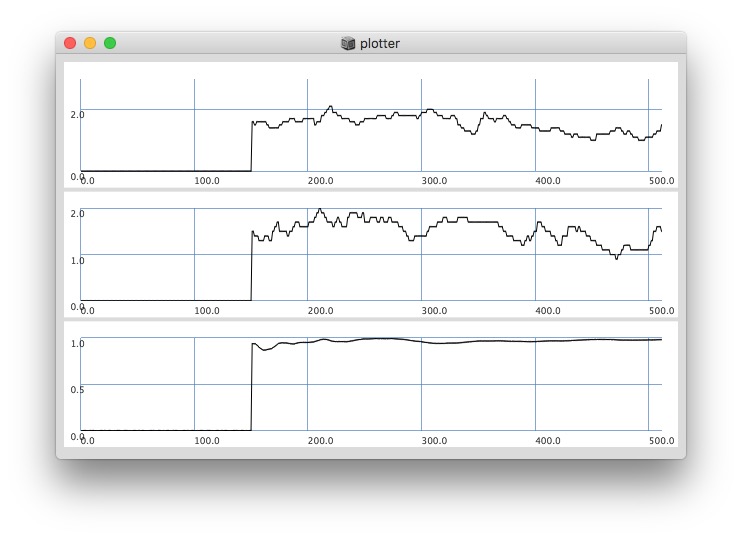
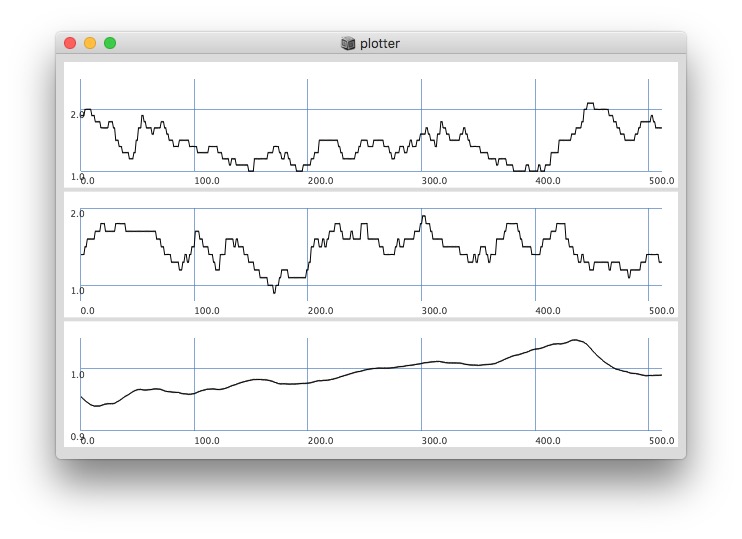
Plotting with different signals (~bandEnergyAvg[6] and ~bandEnergyAvg[7]):
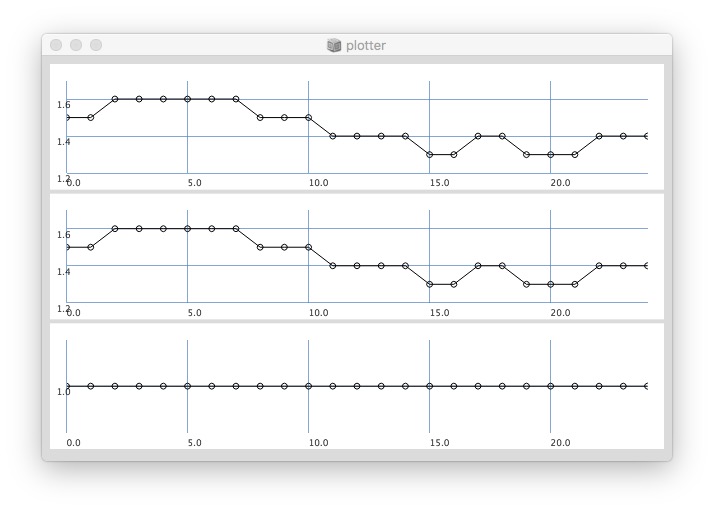
25 sized window:
256 sized window:
// yes the '0’s at start have an effect on the whole ‘coherence’ plot:
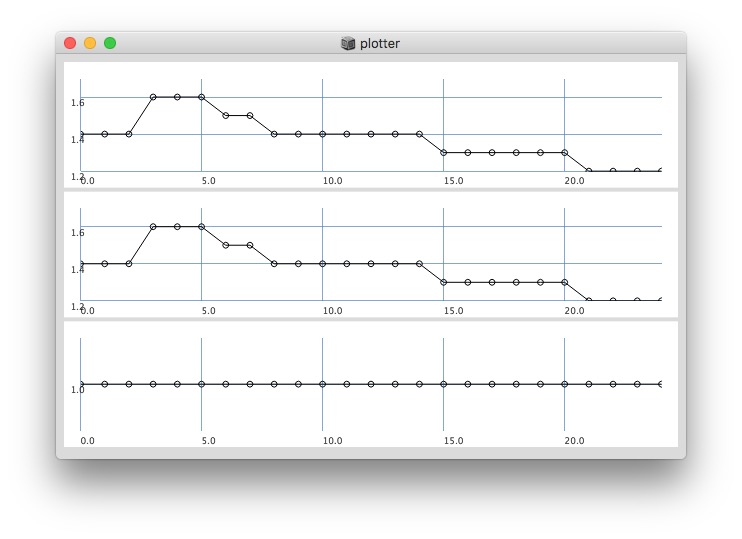
// after '0’s are gone, it changes:
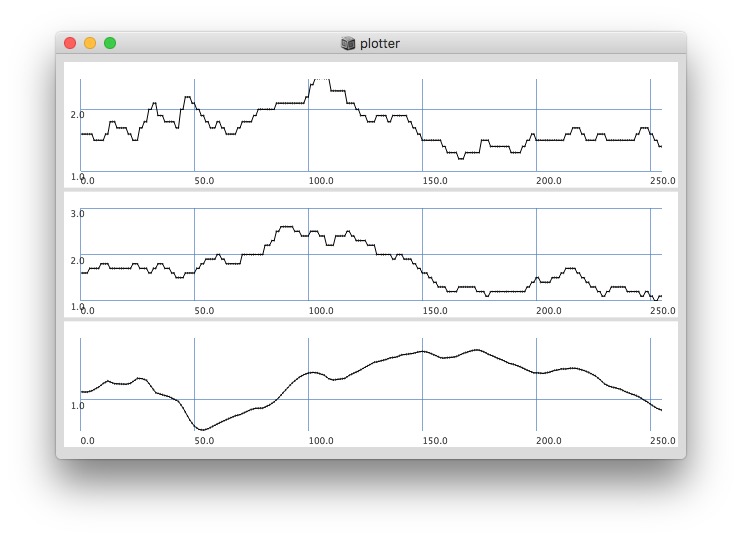
512:
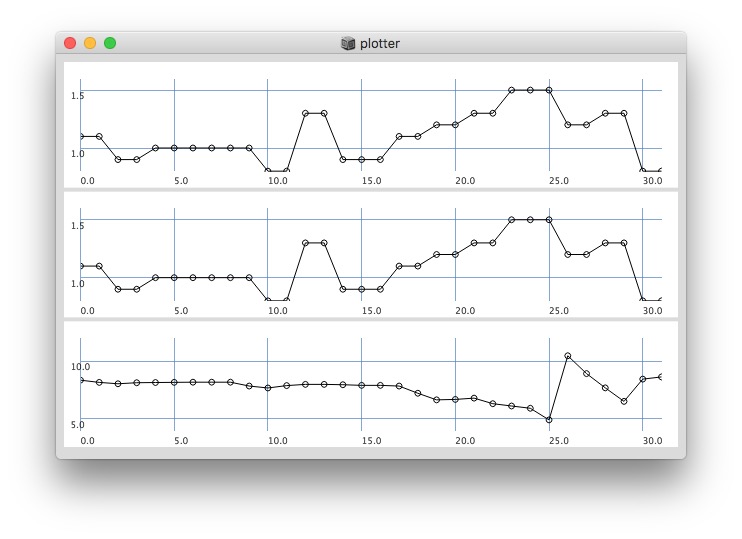
Post window with x, y and a might be interesting as well (512 sized windows):
Signal[ 1.5, 1.5, 1.5, 1.5, 1.5, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2...etc...
Signal[ 1.5, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000...etc...
Signal[ 0.98541378974915, 0.98531132936478, 0.98520904779434, 0.98499572277069, 0.98470383882523, 0.98463100194931, 0.98455816507339, 0.98440420627594, 0.98414701223373, 0.98387265205383, 0.9836984872818, 0.98352444171906, 0.98334735631943, 0.9831702709198, 0.98299318552017, 0.98281615972519, 0.98272758722305, 0.98263907432556, 0.98255050182343, 0.98246198892593, 0.98253279924393, 0.98260360956192, 0.98267447948456, 0.98265677690506, 0.98263907432556, 0.98254013061523, 0.98251914978027, 0.98249816894531, 0....etc...
Signal[ 1.5, 1.5, 1.5, 1.5, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.200000...etc...
Signal[ 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.200000047...etc...
Signal[ 0.98531132936478, 0.98520904779434, 0.98499572277069, 0.98470383882523, 0.98463100194931, 0.98455816507339, 0.98440420627594, 0.98414701223373, 0.98387265205383, 0.9836984872818, 0.98352444171906, 0.98334735631943, 0.9831702709198, 0.98299318552017, 0.98281615972519, 0.98272758722305, 0.98263907432556, 0.98255050182343, 0.98246198892593, 0.98253279924393, 0.98260360956192, 0.98267447948456, 0.98265677690506, 0.98263907432556, 0.98254013061523, 0.98251914978027, 0.98249816894531, 0.98238104581833, 0....etc...
Signal[ 1.5, 1.5, 1.5, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.20000004768...etc...
Signal[ 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.200000047...etc...
Signal[ 0.98520904779434, 0.98499572277069, 0.98470383882523, 0.98463100194931, 0.98455816507339, 0.98440420627594, 0.98414701223373, 0.98387265205383, 0.9836984872818, 0.98352444171906, 0.98334735631943, 0.9831702709198, 0.98299318552017, 0.98281615972519, 0.98272758722305, 0.98263907432556, 0.98255050182343, 0.98246198892593, 0.98253279924393, 0.98260360956192, 0.98267447948456, 0.98265677690506, 0.98263907432556, 0.98254013061523, 0.98251914978027, 0.98249816894531, 0.98238104581833, 0.9822638630867, 0.9...etc...
Signal[ 1.5, 1.5, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1...etc...
Signal[ 1.2999999523163, 1.2999999523163, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.200000047...etc...
Signal[ 0.98499572277069, 0.98470383882523, 0.98463100194931, 0.98455816507339, 0.98440420627594, 0.98414701223373, 0.98387265205383, 0.9836984872818, 0.98352444171906, 0.98334735631943, 0.9831702709198, 0.98299318552017, 0.98281615972519, 0.98272758722305, 0.98263907432556, 0.98255050182343, 0.98246198892593, 0.98253279924393, 0.98260360956192, 0.98267447948456, 0.98265677690506, 0.98263907432556, 0.98254013061523, 0.98251914978027, 0.98249816894531, 0.98238104581833, 0.9822638630867, 0.98214656114578, 0.9...etc...
Signal[ 1.5, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000...etc...
Signal[ 1.2999999523163, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.299999952...etc...
Signal[ 0.98470383882523, 0.98463100194931, 0.98455816507339, 0.98440420627594, 0.98414701223373, 0.98387265205383, 0.9836984872818, 0.98352444171906, 0.98334735631943, 0.9831702709198, 0.98299318552017, 0.98281615972519, 0.98272758722305, 0.98263907432556, 0.98255050182343, 0.98246198892593, 0.98253279924393, 0.98260360956192, 0.98267447948456, 0.98265677690506, 0.98263907432556, 0.98254013061523, 0.98251914978027, 0.98249816894531, 0.98238104581833, 0.9822638630867, 0.98214656114578, 0.98195087909698, 0.9...etc...
Signal[ 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.200000047...etc...
Signal[ 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2999999523163, 1.299999952...etc...
Signal[ 0.98463100194931, 0.98455816507339, 0.98440420627594, 0.98414701223373, 0.98387265205383, 0.9836984872818, 0.98352444171906, 0.98334735631943, 0.9831702709198, 0.98299318552017, 0.98281615972519, 0.98272758722305, 0.98263907432556, 0.98255050182343, 0.98246198892593, 0.98253279924393, 0.98260360956192, 0.98267447948456, 0.98265677690506, 0.98263907432556, 0.98254013061523, 0.98251914978027, 0.98249816894531, 0.98238104581833, 0.9822638630867, 0.98214656114578, 0.98195087909698, 0.9817550778389, 0.98...etc...
Signal[ 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.200000047...etc...
Signal[ 1.3999999761581, 1.3999999761581, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.1000000238419, 1.1000000238419, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2999999523163, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2000000476837, 1.2999999523163, 1.2999999523163, 1.299999952...etc...
Signal[ 0.98455816507339, 0.98440420627594, 0.98414701223373, 0.98387265205383, 0.9836984872818, 0.98352444171906, 0.98334735631943, 0.9831702709198, 0.98299318552017, 0.98281615972519, 0.98272758722305, 0.98263907432556, 0.98255050182343, 0.98246198892593, 0.98253279924393, 0.98260360956192, 0.98267447948456, 0.98265677690506, 0.98263907432556, 0.98254013061523, 0.98251914978027, 0.98249816894531, 0.98238104581833, 0.9822638630867, 0.98214656114578, 0.98195087909698, 0.9817550778389, 0.98157745599747, 0.98...etc...
Many thanks for looking into this… I will carry on thinking…
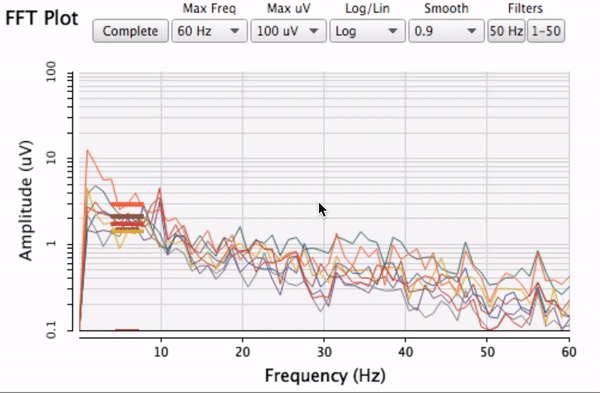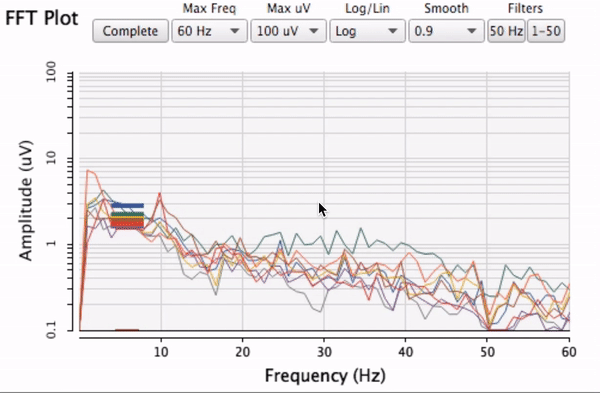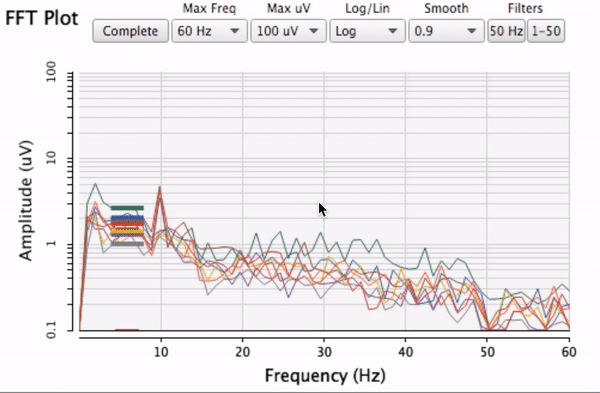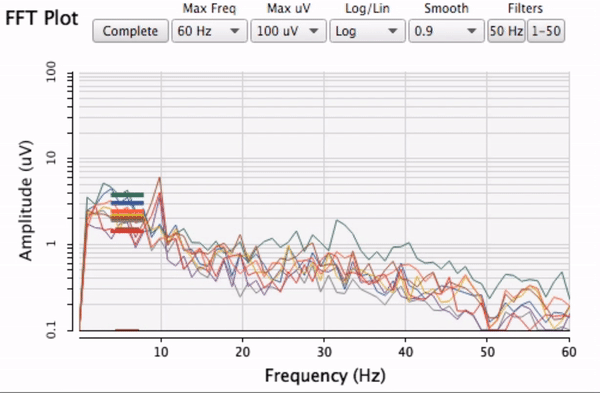

 which is a special case of this where x == y.)
which is a special case of this where x == y.)