Was looking to recreate this as simple as possible… but not sure that InFeedback is doing the trick
(
SynthDef(\sn,{
var input, sig;
input = InFeedback.ar(\out.kr(0),1);
sig = CombN.ar(Blip.ar(input * 300!2, mul:0.5) * Env.perc(0, 0.5).ar(Done.freeSelf), 0.01, 0.01, 0.1);
Out.ar(\out.kr(0), sig);
}).add;
)
Synth(\sn);
any thoughts , insight , advice great appreciated
This synthesis technique heavily relies on single-sample feedback for the resonance.
I would recommend to use Pluck | SuperCollider 3.12.2 Help instead.
Krapp’s Last Karplus Tape
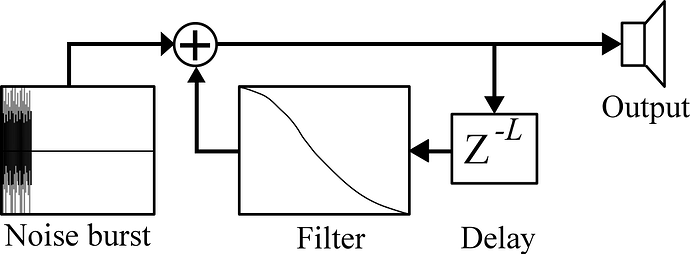
I never liked Karplus-Strong sound 
This is just a Karplus-Strong, but with a spicier SynthDef (extra processing for timbral variety). Scheduling using chaotic equations, prime number base material, and a kind of mathematical acceleration functions to make it sound groovier-ish
s.options.memSize = 65536*4;
s.options.numBuffers = 1024;
s.reboot;
(
SynthDef(\p, {
arg freq = 200, amp = 1.0, pan = 0, pos = 0.15, t = 2.0, b = 0.85;
var exc, str, res;
exc = LPF.ar(Mix([
PinkNoise.ar * Env.perc(0.00232, rrand(0.01, 0.03)).ar * 0.6,
WhiteNoise.ar * Env.perc(0.00124, rrand(0.005, 0.01)).ar * 0.4,
BrownNoise.ar * Env.perc(0.00534, rrand(0.008, 0.009)).ar * 0.3
]), freq * LFNoise1.kr(10.6).range(0.3, 13));
str = Mix.fill(2, { |i|
var d = [0, -0.03].at(i);
Pluck.ar(in: exc, trig: 1, maxdelaytime: 1.0,
delaytime: (freq * (1 + d)).reciprocal,
decaytime: t, coef: b)
});
res = LPF.ar(str, 17000);
res = HPF.ar(res, 120);
res = res + (HPF.ar(res, 4000) * 0.1);
res = res * (1 + (LFNoise2.kr(3) * 0.1));
res = FreqShift.ar(res, LFNoise1.kr(0.2).range(-2, 2));
res = XFade2.ar(
res,
Decimator.ar(res,
rate: LFNoise2.kr(0.3).exprange(12000, 44100),
bits: LFNoise2.kr(1.8).range(3, 24)
),
LFNoise1.kr(0.1) * 0.2
);
DetectSilence.ar(res, doneAction: 2);
Out.ar(0, Pan2.ar(res * amp, pan));
}).add;
~x = {
var bpm = 50;
var f = 100;
var n = 6, t = 1.0; var w = 1.0;
var m = Array.fill(13, { |i| (i+1).nthPrime / (i+2).nthPrime });
var r = Array.fill(n, { rrand(3.7, 3.9999) });
var x = Array.fill(n, { 0.5.rand });
var accelPatterns = [
{|t| t}, // linear
{|t| t * t}, // quadratic acceleration
{|t| t.sqrt}, // quadratic deceleration
{|t| sin(t * pi/2)}, // sinusoidal
{|t| exp(t - 1)}, // exponential
{|t| 1 - cos(t * pi/2)}, // inverse cosine
{|t| t.pow(3)}, // cubic acceleration
{|t| t.pow(1/3)} // cubic deceleration
];
var phaseMods = Array.fill(n, { rrand(0.02, 0.1) });
fork { loop { w = rrand(0.5, 2.0);
t = 0.gauss(6.3).abs * w + 0.1;
rrand(5, 20).wait}};
n.do { |i|
var p = i.linlin(0, n-1, -0.8, 0.8);
var currentPattern = accelPatterns.choose;
var accelPhase = 0;
fork {
loop {
if(0.2.coin) { currentPattern = accelPatterns.choose };
rrand(1,7.0).wait;
}
};
Task({
var baseTime = 60/bpm * (i + 1)/n;
var phaseOffset = 0;
loop {
var f1, c;
var timeWarp;
x[i] = r[i] * x[i] * (1 - x[i]);
c = Complex(0.7, 0.8);
c = c * exp(Complex(0, 0.4 - (6/(1 + x[i].squared))));
f1 = f * m.wrapAt((c.real.abs * 13).floor) * [0.17, 0.593, 0.866, 1, 1.25, 1.42, 9.3].choose * rrand(0.98, 1.12);
accelPhase = (accelPhase + phaseMods[i]).wrap(0, 1);
timeWarp = currentPattern.(accelPhase);
Synth(\p, [
\freq, f1 * (1 + 0.001.rand2),
\amp, c.real.abs.clip(0.1, 0.3),
\t, c.imag.abs.clip(0.9, 2.0),
\pos, x[i].wrap(0.1, 0.9),
\b, c.real.abs.wrap(0.2, 0.7),
\pan, p + (0.1.rand2)
]);
(baseTime * c.real.abs.clip(0.5, 1.5) * t * timeWarp).wait;
if(0.05.coin) {
accelPhase = 0;
if(0.3.coin) { currentPattern = accelPatterns.choose };
};
}
}).play;
};
};
)
// start
~x.();
Nice chaotic sound:) As a side question, I often find code in the help files or examples like this that don’t stop on command + period (for mac) but I also have a feeling that command + period does not work the same on every system or configuration. Often - but not always, it seems - this is the case for a Pbind not assigned to a variable. Even after quitting the server, the routine is still running resulting in loads of error messages after reboot, only way out seems to be recompiling the library. Does anybody have any insights on this?
I think it should not happen unless there is some failure in the server for some reason. Most of the time, you can increase server resources to fix this.
(Maybe happens here because this is a bit nuts)
I has been consistently this way since I started using SC 4 years ago. This is in my startup file:
s.options
.memSize_(2.pow(21))
.numWireBufs_(256)
.blockSize_(64)
.sampleRate_(48000)
.hardwareBufferSize_(128)
.numOutputBusChannels_(2);
Which of these settings could affect the behaviour described?
I increased memSize. After that, it ran for a long time without errors, and the CPU remained acceptable, but it varied a lot, too (from 5% up to 40%)
I thought that memsize = 2 ** 21 was already overkill…I will try numWireBufs but I doubt it will make a difference. Some of the cases I talk about are very basic Pbinds examples from the help files with nothing fancy going on.
It sounds like something we should examine closer! Which code and which failures are going on there? Simple Pbind examples?
Sorry for hijacking this thread, I will start a new one with the issue and see if other users are experiencing the same issues.
Check if there is an issue open on GH. I think that’s the protocol. However, the forum has more eyes; one can feel it if it happens with other users—both help.
Also, still repeating the protocol, give all the information. Is it the develop branch or stable release? What code? What failure? What’s the minimal example that triggers that? etc
some good sounds
I was looking to use the Karplus - Strong to make different percussive sounds
The basics are here; you can tweak many things and get very different sounds, too.
thank you! excited dive into this
Here is the most canonical Karplus-Strong I can come up with, without using extensions – basically a 1:1 implementation of the block chart.
s.options.blockSize = 16; // extend the upper frequency limit
s.boot;
(
SynthDef(\basicks, { |out, gate = 1, amp = 0.1, freq = 440, decay = 1,
excAtk = 0.001, excDcy = 0.005,
ffreq = 8000|
var feedback = LocalIn.ar(1); // don't need InFeedback
// n repetitions = freq * decay
// we want coeff ** n = 0.001, so coeff = 0.001 ** (1/n)
var coeff = 0.001 ** (freq * decay).reciprocal;
var excEnv = EnvGen.ar(Env.perc(excAtk, excDcy));
var mainEnv = EnvGen.ar(Env.asr(0, 1, 0.03), gate + 0.001, doneAction: 2);
var exc = PinkNoise.ar * excEnv;
var sig;
// filter must be inside the feedback-delay loop
feedback = LPF.ar(feedback, ffreq) * coeff;
sig = DelayC.ar(exc + feedback, 0.5, freq.reciprocal - ControlDur.ir);
LocalOut.ar(sig); // --> back to LocalIn
DetectSilence.ar(sig, doneAction: 2);
Out.ar(out, (sig * (mainEnv * amp)).dup);
}).add;
)
(
p = Pbind(
\instrument, \basicks,
\degree, Pwhite(-7, 7, inf),
\dur, Pexprand(0.08, 0.5, inf),
\decay, Pexprand(0.3, 9.0, inf),
\ffreq, Pexprand(5000, 16000, inf)
).play;
)
p.stop;
Not necessarily. Without single-sample feedback, there is an upper limit on note frequency = sr / blocksize, e.g. my example is running on my system at 48 kHz, divided by blockSize = 16, so I can play up to 3000 Hz. Without changing the block size, that limit would go down to 750 Hz.
Within the frequency limit, KS works perfectly well. There is no strict requirement for single-sample feedback.
Using an extension for single-sample feedback, e.g. Feedback quark, would push the upper frequency limit arbitrarily high (within Nyquist).
hjh
yes canonical is what I was trying to understand, Pluck is def made for it but in terms of understand how it works this is incredibly helpful. thank you !
Just to add:
The reason that the filter beeing implemented in the block diagram of Karplus-Strong is typically a OnePole filter, is that its not adding additional delay into the feedback path. In my opinion the default choice for adding a filter into a feedback path should be a OnePole filter. It doesnt matter all that much here, but just if one dont know you can calculate the coefficients for a OnePole filter like this, you can also derive an allpass:
lowpass = OnePole.ar(sig, exp(-2pi * fltCutOff * SampleDur.ir));
highpass = sig - OnePole.ar(sig, exp(-2pi * fltCutOff * SampleDur.ir));
The simplest form of a filter is a OnePole filter. It can be implemented by a weighted average (linear crossfade) of your unfiltered input with its single-sample feedback, where a mix param between 0 and 1 is determining the blending of the two signals. A typical higher order filter can be for example based on a biquad core which has two feedforward and two feedback sample delay paths and is therefore of the order 2.
The order of the filter determines how steep its cutoff is. The higher the order of the filter is, the steeper is its cutoff, but the higher is the number of samples of delay which are added.
Thats a cool insight, thanks!
That’s fair… I don’t have a particularly compelling reason for using the second-order LPF in my example, just lazy I guess.
For KS, it’s even fine to specify the one-pole coefficient directly as a damping parameter.
Thanks for the correction –
hjh