Mimic this filter with Supercollider

Questions
1

Hi, Most of my experience with filters has been in DAWs using native or VST EQs. And I’m trying to transpose that experience within SC. I find it hard to match the controls I have in my VST to the ones in SC.

For example:
filter

How can I translate (roughly) this into SC UGens ?

For now I’m using a BHiPass (despite it being a -12db slope while my initial filter is a -4.4db slope):
sig = BHiPass.ar(sig,freq,\freqboost.kr(13).dbamp/freq);

Actually, I don’t understand :

  • how to compute the rq field from “Resonance(db)”
  • how to get the desired filter slope

I listed many of the existing filters in SC, and, none seems to match the one of my VST…

This might be obvious for most of me but it remains a bit cryptic for me…

2

This doesn’t answer the filter design question, but… have you tried VSTPlugin?

Something like this:

(
SynthDef(\vstfx, { |out = 0|
	var sig = In.ar(out, 2);  // EDIT: treat as inline effect
	sig = VSTPlugin.ar(sig, numOut: 2);
	ReplaceOut.ar(out, sig);
}).add;
)

s.boot;
VSTPlugin.search;

a = Synth(\vstfx);
c = VSTPluginController(a);
c.open("NeatoFilterWhoseNameIsHiddenInTheImage.vst3");  // or .vst
c.editor;

// set the controls in the interface

c.writeProgram("... where do I want to save my filter preset? ...");

c.close;
a.free;


// then, next time
a = Synth(\vstfx);
c = VSTPluginController(a);

(
c.open("NeatoFilterWhoseNameIsHiddenInTheImage.vst3", action: { |vstctl, success|
	if(success) {
		c.readProgram("... preset path...");
	} {
		Error("VST plugin loading failed").throw;
	}
});
)

VSTPluginController has interfaces for setting parameters from SC, too.

hjh

1 Like
3

I can second @jamshark70’s recommendation :wink:

Use the right tool for the job! Of course, it is possible to implement good EQs (or Compressors, or Limiters, etc.) in SuperCollider, but why bother? If you already have a nice EQ plugin, by all means use it! Then you have more time to focus on the important (and novel!) parts of your project.

If you want to replicate the EQ plugin for learning purposes, that’s a different story, of course!

4

I’ve already used VST for other projects. And it is so easy.
My purpose is here mostly to learn to use the EQs in SC. How to translate my (limited) knowledge of EQ to the concepts of SC.

2 Likes
5

Match as in ‘null when the phase is flipped’?
There is no guarantee that it will.
There is no standard way to implement a filter, instead, there are many different varieties, and even then, the plugin author may have decided to add non-standard parts (perhaps some subtle saturation).

That being said…

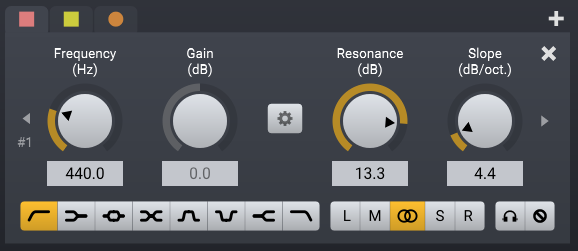
rq is the reciprocal of q, which is the bandwidth/cutoffFreq. Is resonance the some thing as q… maybe? It depends on what the plugin designer did. Perhaps the number for the setting shown in the picture would be 1/13.3, but its impossible to tell.

The Slope is even more complex as they have a knob for increasing slope. The built in filters do not support this. Instead, in super collider, you can double the slope by duplicating the filter in series. BHiPass4 does this for you. This is called the order of the filter - BHiPass is a 2nd order filter and gives 12db/oct, BiHiPass4 is a 4th order and gives 24db/oct. Therefore each order is 6db/oct. I think - hopefully some one will correct me if I’m wrong - that you can add another filter in series, and blend it with the previous signal to get factional amounts? I have no idea if this will create odd phasing issues having not dived into filter design too much.

The frequency is generally agreed to be some fixed reduction point, I imagine this will line up with all the supercollide ugens, but again, no guarantee.

I’m not too sure what the overlapping circles mean, is that bar: left, mid, stereo, side, right? Not too sure what thats about.

So, I’d guess the correct way (without slope) to implement this would be…

BHiPass.ar(sig, \freq.kr, \resonance.kr.reciprocal, \gain.kr(0).dbamp.sanitize )

Now with the slope - and I’m really guessing here…

x = {
	var max_slope = 24;                         // can change this if needed
	var slope_per_filter = 6;                   // fixed by BHiPass
	var num_filters = max_slope / slope_per_filter;
	
	var slope = \slope.kr(0).clip(0, max_slope);
	
	var lerp = (1..num_filters).collect{ |n| 
		(slope_per_filter + slope - (n*slope_per_filter)) / slope_per_filter   // in db not amps, probably wrong
	}.clip(0,1);
	
	var filter_bank = lerp.collect{ |l|    // an array of functions
		{|in| 
			var rq = 1.blend(\resonance.kr(4).clip(0.00001, inf).reciprocal, l);
			var f = BHiPass.ar(in, \freq.kr(220), rq);
			in.blend(f, l)
		}
	};
	
	var sig = WhiteNoise.ar();
	
	filter_bank.inject(sig, {|i, f| f.(i) }) * \gain.kr(0).dbamp.sanitize;
	
}.play

x.set(\slope, 0)
x.set(\freq, 1500)
x.set(\resonance, 36)
x.set(\gain, -10)
1 Like
7

Thanks for your answers. Let me some time to digest this, go deeper into transfer functions, complex frequency and above all experiment with this !

8

If you don’t already know it, I would recommend checking out Dan Worrall’s YT channel - he’s responsible for the FabFilter plugin demos (and I think he’s done some of the Waves promo as well). His channel is full of filter theory, plugin design theory, and it’s presented in a way that could easily be translated to SC. If you’re lucky, he’s already done an analysis of your VST; then you’ll definitely get some insight into what that Resonance knob is doing!

3 Likes
9

This is from the filter design book writer. It’s a bit of a chore trying to gather the resources to learn this online, so an actual course might help.

4 Likes