This question has been raised in the video, and I wondered why it was actually raised, for several reasons. Please let me try to explain.
Effort
I think we agree that in case of a 2 operator stack, the modulator modulates the phase of the carrier like this:
mod = SinOsc.ar(freq: car_freq * mod_ratio);
car = SinOsc.ar(freq: car_freq, phase: mod_index * mod);
If this is correct, I doubt that Yamaha has implemented the 3 operator stack differently. Wouldn’t it be inefficient to implement different ways on how an operator interprets incoming phase data depending on whether or not a modulator is modulating a carrier or a modulator? Given the limited resources, I find this hard to imagine. But I am not an engineer, I may be wrong.
Sound
So instead of theoretical musings, I’ll try an audible example. This rendition of one of the DX7’s more popular sounds, Preset 26 “TUB BELLS”, is extremely poor, but hopefully good enough to do the trick:
(
SynthDef(\PM_2OP_Tubular, {
arg car_freq=200, mod_ratio=3.5, mod_index=2;
var env, car, mod;
env = EnvGen.kr(envelope: Env.perc(releaseTime: 4), doneAction: 2);
mod = SinOsc.ar(freq: car_freq * mod_ratio) * env;
car = SinOsc.ar(freq: car_freq, phase: mod_index * mod) * env;
Out.ar(0, car!2 * 0.2);
}).play
)
Now let’s put one operator below this 2 operator stack. To make this test more obvious, I’ll use the fixed frequency setting for this new operator. This DX7 feature allowed to decouple an operator’s frequency from the keyboard and set it to an arbitrary fixed frequency between 0.1 and 9772 Hz. With very slow frequencies it was used for chorus- or PWM-like effects. With the bells on top, it sounds like this:
(
SynthDef(\PM_3OP_Tubular, {
arg car_freq=200, mod_ratio=3.5, mod_index=2;
var env, new_car, car, mod;
env = EnvGen.kr(envelope: Env.perc(releaseTime: 4), doneAction: 2);
mod = SinOsc.ar(freq: car_freq * mod_ratio) * env;
car = SinOsc.ar(freq: car_freq, phase: mod_index * mod) * env;
new_car = SinOsc.ar(freq: 1, phase: car) * env;
Out.ar(0, new_car!2 * 0.2);
}).play
)
Which is how it would have sounded on my old DX7 if I still had it.
Now let’s try the suggested alternatives, first the addition (as I understand it, please correct me if I am wrong):
(
SynthDef(\PM_3OP_Tubular_mix, {
arg car_freq=200, mod_ratio=3.5, mod_index=2;
var env, new_car, car, mod;
env = EnvGen.kr(envelope: Env.perc(releaseTime: 4), doneAction: 2);
mod = SinOsc.ar(freq: car_freq * mod_ratio) * env;
car = SinOsc.ar(freq: car_freq) * env;
new_car = SinOsc.ar(freq: 1, phase: car + mod) * env;
Out.ar(0, new_car!2 * 0.2);
}).play
)
Which sounds one octave lower, also the harmonic structure is duller. So I doubt that this addition is the right way to mimic serial 3 operator stacks.
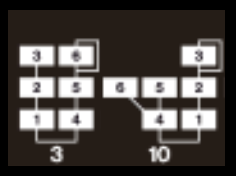
It is not a wrong way in itself though, as the DX7 offered dedicated algorithms to accomplish such parallel mixture, see e.g. operators 4,5 and 6 in algorithm 10:
Now on to the other suggested alternative, the multiplication (again, as I understand it, please correct me if I am wrong):
(
SynthDef(\PM_3OP_Tubular_mul, {
arg car_freq=200, mod_ratio=3.5, mod_index=2;
var env, new_car, car, mod;
env = EnvGen.kr(envelope: Env.perc(releaseTime: 4), doneAction: 2);
mod = SinOsc.ar(freq: car_freq * mod_ratio) * env;
car = SinOsc.ar(freq: car_freq, mul: mod_index * mod) * env;
new_car = SinOsc.ar(freq: 1, phase: car) * env;
Out.ar(0, new_car!2 * 0.2);
}).play
)
Also a considerably different harmonic structure.
This is why I am convinced that phase input signals are handled equally in all operators, independent of their positions in the stack: Each one is modulating the phase of the one below it. Phase input signals are mixed/added in case operators are going in parallel into an operator below. But I think we can rule out multiplication. What do you think?