hey,
about two or three years ago i came across a library of single cycle waveforms by Christian Vogel, which is shipped with the nuPG.
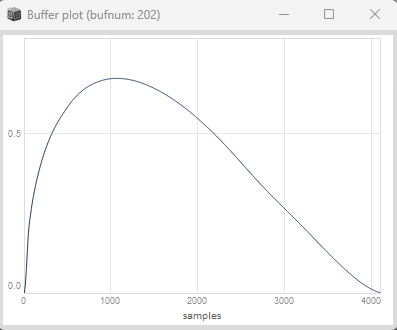
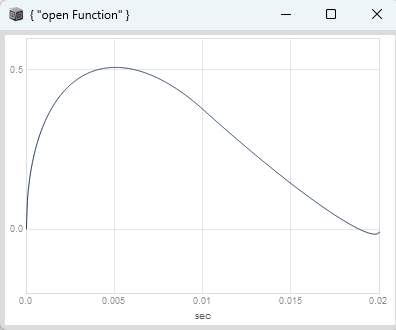
At the time i was investigating different waveforms for phase increment distortion in the context of pulsar synthesis to shape the phase of the pulsaret for a frequency trajectory per grain. The one which by far sounded the best (and thats kind of cute <3) was the halfAHeart window. It actually looks kind of similar to an analog RC envelope with convex rise during attack time.
Here it is:
After finding things by accident i always try to parameterize them, for the greater possibility of variation.
This might be the longest post i have ever written, so follow me down the rabbit hole. I will share some discoveries i have made along the way ![]()
So lets start at the beginning.
The core concept we are dealing with here is phase shaping vs. phase increment distortion.
Here are two papers about this topic:
1.) Adaptive Phase Distortion Synthesis
2.) Phase and Amplitude Distortion Methods for Digital Synthesis of Classic Analogue
Waveforms
phase shaping vs. phase increment distortion
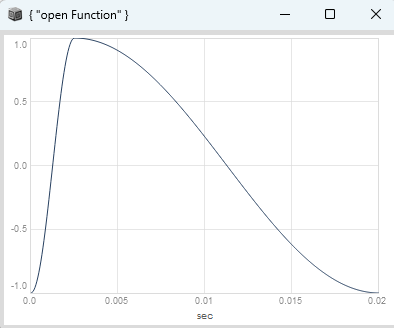
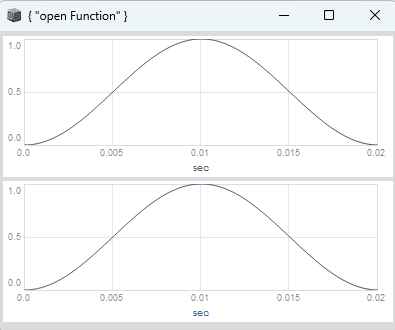
You might be familiar with phase distortion in the yamaha synthesizers from the 80s, where you have a sinusoidal oscillator which you can morph into a saw wave like this:
phase shaping
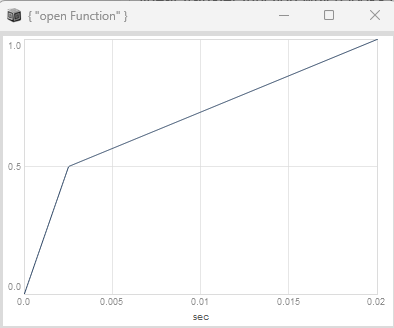
The classic phase distortion (PD) formula can be implemented as phase shaping by applying a segmented non-linear transfer function with a kink, which goes from 0 to 0.5 with one slope and then from 0.5 to 1 with another slope, with control over the skew parameter, which offsets the kink from the center position at 0.5 (no kink) either to the left or the right. It looks like this for a skew value of 0.125.
Here is how you can implement phase shaping for classic PD:
(
var kink = { |phase, skew|
Select.ar(phase > skew, [
0.5 * (phase / skew),
0.5 * (1 + ((phase - skew) / (1 - skew)))
]);
};
{
var skew = \skew.kr(0.125);
var phase = Phasor.ar(0, 50 * SampleDur.ir);
var warpedPhase = kink.(phase, skew);
cos(warpedPhase * 2pi).neg;
}.plot(0.02);
)
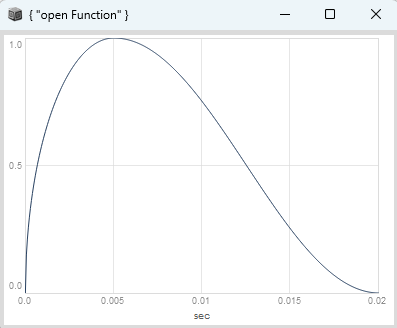
phase increment distortion
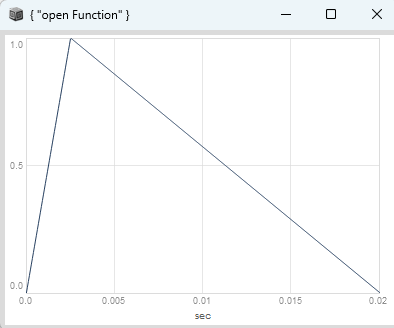
The classic phase distortion (PD) can also be implemented as phase increment distortion, where you add a triangular non-linear modulation term to your linear phase, which goes from 0 to 1 with one slope and back to 0 with another slope, with control over the skew parameter, which offsets the triangle peak from the center position at 0.5 (both slopes are the same) to the left or right.
It looks like this for a skew value of 0.125.
Here is how you can implement phase increment distortion for classic PD:
(
var triangle = { |phase, skew|
Select.ar(phase > skew, [
phase / skew,
1 - ((phase - skew) / (1 - skew))
]);
};
{
var skew = \skew.kr(0.125);
var phase = Phasor.ar(0, 50 * SampleDur.ir);
var warpedPhase = triangle.(phase, skew);
cos(phase + (warpedPhase * (0.5 - skew)) * 2pi).neg;
}.plot(0.02);
)
conclusion
Its worth noting that phase increment distortion is a subset of phase modulation, with the difference that the modulational index is only dependend on the skew param and is not added to the phase modulator explicitly.
We can further note that both techniques phase modulation and phase increment distortion produce identical results.
The implementation for the kink and the triangle function i have chosen is identical to:
var kink = { |phase, skew|
phase = phase.linlin(0, 1, skew.neg, 1 - skew);
phase.bilin(0, skew.neg, 1 - skew, 0.5, 0, 1);
};
var triangle = { |phase, skew|
phase = phase.linlin(0, 1, skew.neg, 1 - skew);
phase.bilin(0, skew.neg, 1 - skew, 1, 0, 0);
};
But i find using the combination of .linlin and .bilin way less intuitive to grasp whats actually happening.
Before we create the synthesized version of the halfAHeart window, i would like to share a neat dsp trick with you, which i have learned from the GO book. If you want to synthesize a symmetrical waveform, you just have to synthesize one side of it and can mirror it by driving it with a triangular phase. If we use our triangle function for this, we can bend that waveform to the left or the right, like we would do in phase distortion synthesis, depending on the skew parameter.
Here shown by applying a linear ramp signal to an ordinary hanning window, while a triangle shaped phase is applied to a unit hanning window. The results for skew = 0.5 are identical, but you are able to skew the unitHanning version to the left or the right:
(
var triangle = { |phase, skew|
Select.ar(phase > skew, [
phase / skew,
1 - ((phase - skew) / (1 - skew))
]);
};
var unitHanning = { |phase|
1 - cos(phase * pi) * 0.5;
};
var hanning = { |phase|
1 - cos(phase * 2pi) * 0.5;
};
{
var phase = Phasor.ar(0, 50 * SampleDur.ir);
var warpedPhase = triangle.(phase, \skew.kr(0.5));
var hanningA = unitHanning.(warpedPhase);
var hanningB = hanning.(phase);
[hanningA, hanningB];
}.plot(0.02);
)
parameterizing the halfAHeart Window for phase increment distortion
The halfAHeart window, found in the single cycle waveform pack by Christian Vogel can be implement like this:
(
var triangle = { |phase, skew|
Select.ar(phase > skew, [
phase / skew,
1 - ((phase - skew) / (1 - skew))
]);
};
var unitHanning = { |phase|
1 - cos(phase * pi) * 0.5;
};
var unitCircular = { |phase|
sqrt(phase * (2 - phase));
};
var halfAHeart = { |phase, skew|
var warpedPhase = triangle.(phase, skew);
var hanning = unitHanning.(warpedPhase);
var circular = unitCircular.(warpedPhase);
Select.ar(phase > skew, [
circular,
hanning
]);
};
{
var phase = Phasor.ar(0, 50 * SampleDur.ir);
halfAHeart.(phase, \skew.kr(0.25));
}.plot(0.02);
)
Its a combination of a circular easeOut function for the first segment, followed by a sinusoidal easeIn function. Worth noting is that the window now is perfectly normalized between 0 and 1 and that for a skew parameter of 0.25 it produces a smooth transition in slope from the first segment to the next.
After i had synthesized the halfAHeart window function, i came across the concept of easing functions and particularly the easingOutIn which is often times called a seat.
easingOutIn or seat
With an easingOutIn or easingSeat you are composing a transfer function out of an easingOut and an easingIn function. For a cubic core function into an easingSeat function with adjustable height this could look like this:
(
var easeIn = { |x|
x * x * x;
};
var easeOutIn = { |x, height = 0.5|
Select.ar(x > 0.5, [
height - (height * easeIn.(1 - (x * 2))),
height + ((1 - height) * easeIn.((x - 0.5) * 2))
]);
};
var cubicSeatReversedToLinear = { |x, shape, height = 0.5|
var mix = shape * 2;
var easeOut = 1 - easeOutIn.(1 - x, height);
easeOut * (1 - mix) + (x * mix);
};
var linearToCubicSeat = { |x, shape, height = 0.5|
var mix = (shape - 0.5) * 2;
var easeIn = easeOutIn.(x, height);
x * (1 - mix) + (easeIn * mix);
};
var cubicSeatToLinearMorph = { |x, shape, height = 0.5|
Select.ar(shape > 0.5, [
cubicSeatReversedToLinear.(x, shape, height),
linearToCubicSeat.(x, shape, height)
]);
};
{
var phase = Phasor.ar(DC.ar(0), 50 * SampleDur.ir);
var sigA = cubicSeatToLinearMorph.(phase, \shapeA.kr(0), \height.kr(0.875));
var sigB = cubicSeatToLinearMorph.(phase, \shapeB.kr(0.5), \height.kr(0.875));
var sigC = cubicSeatToLinearMorph.(phase, \shapeC.kr(1), \height.kr(0.875));
[sigA, sigB, sigC];
}.plot(0.02).superpose_(true).plotColor_([Color.red, Color.blue, Color.magenta]);
)
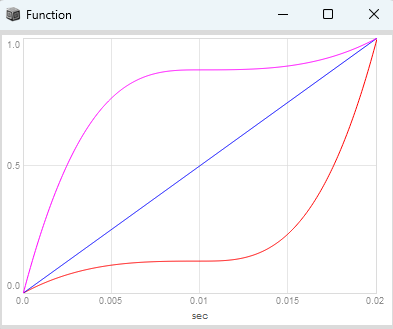
easing towards halfAHeart
After discovering easingOutIn functions with adjustable height, i found out that if you implement our synthesized halfAHeart window with a skew value of 0.25 as phase increment distortion and plot it aside these easingOutIn functions (one with a cubic and one with a circular core) implemented as phase shaping you get more or less the same results (beside what i have said earlier i have implemented the phase increment distortion with an index of 2 here, which results in this particular case of skew 0.25 to an index which is independent from the actual skew value. That was exactly the version you could hear in the sound example in the beginning):
(
// heart easing window
var triangle = { |phase, skew|
Select.ar(phase > skew, [
phase / skew,
1 - ((phase - skew) / (1 - skew))
]);
};
var unitHanning = { |phase|
1 - cos(phase * pi) * 0.5;
};
var unitCircular = { |phase|
sqrt(phase * (2 - phase));
};
var halfAHeart = { |phase, skew|
var warpedPhase = triangle.(phase, skew);
var hanning = unitHanning.(warpedPhase);
var circular = unitCircular.(warpedPhase);
Select.ar(phase > skew, [
circular,
hanning
]);
};
//////////////////////////////////////////////////////
// cubic seat
var cubicIn = { |x|
x * x * x;
};
var cubicOutIn = { |x, height = 0.5|
Select.ar(x > 0.5, [
height - (height * cubicIn.(1 - (x * 2))),
height + ((1 - height) * cubicIn.((x - 0.5) * 2))
]);
};
var cubicSeatReversedToLinear = { |x, shape, height = 0.5|
var mix = shape * 2;
var easeOut = 1 - cubicOutIn.(1 - x, height);
easeOut * (1 - mix) + (x * mix);
};
var linearToCubicSeat = { |x, shape, height = 0.5|
var mix = (shape - 0.5) * 2;
var easeIn = cubicOutIn.(x, height);
x * (1 - mix) + (easeIn * mix);
};
var cubicSeatToLinearMorph = { |x, shape, height = 0.5|
Select.ar(shape > 0.5, [
cubicSeatReversedToLinear.(x, shape, height),
linearToCubicSeat.(x, shape, height)
]);
};
//////////////////////////////////////////////////////
// circular seat
var circularIn = { |x|
1 - sqrt(1 - (x * x));
};
var circularOutIn = { |x, height = 0.5|
Select.ar(x > 0.5, [
height - (height * circularIn.(1 - (x * 2))),
height + ((1 - height) * circularIn.((x - 0.5) * 2))
]);
};
var circularSeatReversedToLinear = { |x, shape, height = 0.5|
var mix = shape * 2;
var easeOut = 1 - circularOutIn.(1 - x, height);
easeOut * (1 - mix) + (x * mix);
};
var linearToCircularSeat = { |x, shape, height = 0.5|
var mix = (shape - 0.5) * 2;
var easeIn = circularOutIn.(x, height);
x * (1 - mix) + (easeIn * mix);
};
var circularSeatToLinearMorph = { |x, shape, height = 0.5|
Select.ar(shape > 0.5, [
circularSeatReversedToLinear.(x, shape, height),
linearToCircularSeat.(x, shape, height)
]);
};
{
var skew = 0.25;
var height = 0.875;
var shape = 1;
var phase = Phasor.ar(0, 50 * SampleDur.ir);
var heartEase = phase + (halfAHeart.(phase, skew) * (0.5 - skew) * \index.kr(2));
var circular = circularSeatToLinearMorph.(phase, shape, height);
var cubic = cubicSeatToLinearMorph.(phase, shape, height);
[heartEase, circular, cubic];
}.plot(0.02).superpose_(true).plotColor_([Color.red, Color.blue, Color.magenta]);
)
Whats really interesting is, that the halfAHeart window implemented as phase increment distortion with a skew value of 0.25 and the easingSeat function with a height value of 0.875 are meeting at the unit circle at 0.5 on the x axis (here 0.01 seconds).
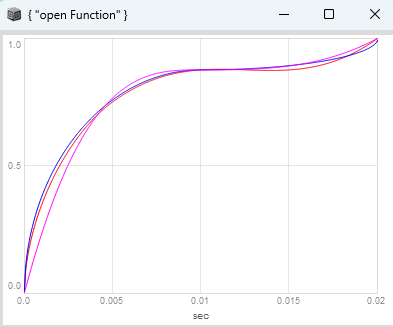
and now we are doing a full circle: if you substract the linear phase from your circular easingSeat function implemented as phase shaping, which is the most close to the synthesized halfAHeart window you get:
(
var circularIn = { |x|
1 - sqrt(1 - (x * x));
};
var circularOutIn = { |x, height = 0.5|
Select.ar(x > 0.5, [
height - (height * circularIn.(1 - (x * 2))),
height + ((1 - height) * circularIn.((x - 0.5) * 2))
]);
};
var circularSeatReversedToLinear = { |x, shape, height = 0.5|
var mix = shape * 2;
var easeOut = 1 - circularOutIn.(1 - x, height);
easeOut * (1 - mix) + (x * mix);
};
var linearToCircularSeat = { |x, shape, height = 0.5|
var mix = (shape - 0.5) * 2;
var easeIn = circularOutIn.(x, height);
x * (1 - mix) + (easeIn * mix);
};
var circularSeatToLinearMorph = { |x, shape, height = 0.5|
Select.ar(shape > 0.5, [
circularSeatReversedToLinear.(x, shape, height),
linearToCircularSeat.(x, shape, height)
]);
};
{
var phase = Phasor.ar(0, 50 * SampleDur.ir);
circularSeatToLinearMorph.(phase, \shape.kr(1), \height.kr(0.875)) - phase;
}.plot(0.02);
)
Which seems to have some similiar features to the initial halfAHeart single cycle waveform from the sample pack (look at the amplitudes, not beeing normalized between 0 and 1 anymore).
little easter egg:
Vector-Phase-Shaping implemented with phase shaping
(
var transferFunc = { |phase, harm, skew|
phase = phase.linlin(0, 1, skew.neg, 1 - skew);
phase.bilin(0, skew.neg, 1 - skew, harm, 0, 1);
};
var vps = { |freq, skew, harm|
var phase = Phasor.ar(DC.ar(0), freq * SampleDur.ir);
var harm_even = harm.round(2);
var harm_odd = ((harm + 1).round(2) - 1);
var phasor_even = transferFunc.(phase, harm_even, skew);
var phasor_odd = transferFunc.(phase, harm_odd, skew);
var sig_even = cos(phasor_even * 2pi).neg;
var sig_odd = cos(phasor_odd * 2pi).neg;
LinXFade2.ar(sig_even, sig_odd, harm.fold(0, 1) * 2 - 1);
};
{
var freq = 55;
var skew = MouseX.kr(0.01, 0.99);
var harm = MouseY.kr(1.0, 10.0);
var sig = vps.(freq, skew, harm);
sig = LeakDC.ar(sig);
sig !2 * 0.1;
}.play;
)
Vector-Phase-Shaping implemented with phase increment distortion
(
var transferFunc = { |phase, skew|
Select.ar(phase > skew, [
phase / skew,
1 - ((phase - skew) / (1 - skew))
]);
};
var vps = { |freq, skew, harm|
var phase = Phasor.ar(DC.ar(0), freq * SampleDur.ir);
var harm_even = harm.round(2);
var harm_odd = ((harm + 1).round(2) - 1);
var pmod = transferFunc.(phase, skew);
var sig_even = cos(phase + (pmod * (harm_even - skew)) * 2pi).neg;
var sig_odd = cos(phase + (pmod * (harm_odd - skew)) * 2pi).neg;
LinXFade2.ar(sig_even, sig_odd, harm.fold(0, 1) * 2 - 1);
};
{
var freq = 55;
var skew = MouseX.kr(0.01, 0.99);
var harm = MouseY.kr(1.0, 10.0);
var sig = vps.(freq, skew, harm);
sig = LeakDC.ar(sig);
sig !2 * 0.1;
}.play;
)