I know that Phasor is a rather delicate class, especially when modulating.
But during a deep dive/debug session of another project I found this behavior which I could not explain and I am unsure if this is a bug or not.
The setup is easy - use two phasors but one is offset by a sub-sample and simply take a look at their difference, which should be simply the offset right? Well, it’s not.
The code is
(
// why is this not constant?
{
var numSamples = s.sampleRate * 4;
var phasor1 = Phasor.ar(trig: 0, rate: 1, start: 0, end: numSamples);
var phasor2 = Phasor.ar(trig: 0, rate: 1, start: 0.2, end: numSamples);
phasor2-phasor1;
}.plot(4);
)
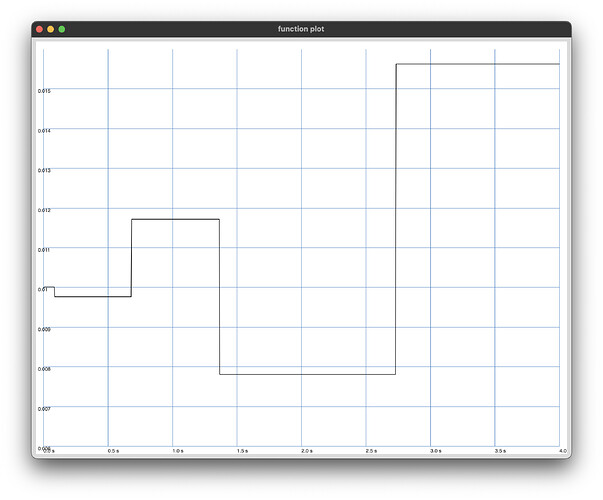
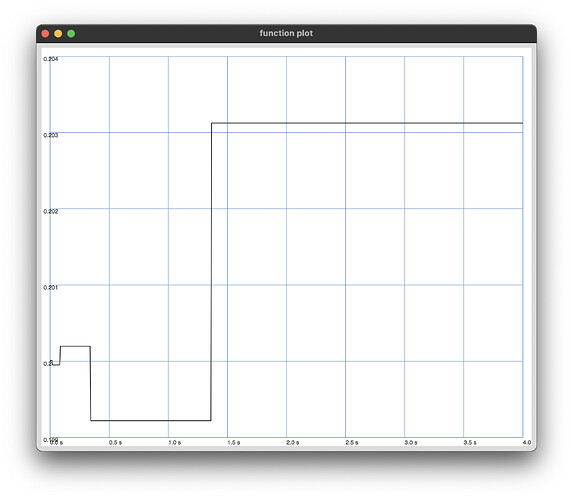
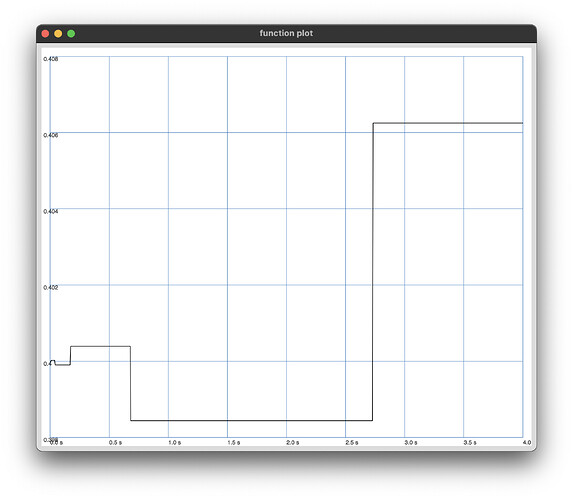
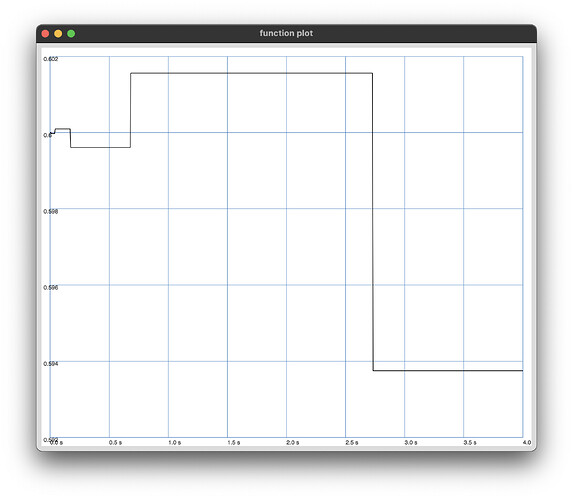
and results in the following plots
start: 0.01 (nearly 50% off!)
start: 0.2
start: 0.4
start: 0.6
Can someone explain why there is a fluctuation of the delta which is quite measurable?
Good question.
First of all to make sure we are not seeing a bug, here is a simple C++ program which approximates the behavior of phasor. On my machine, this produces the exact same output as Phasor in SC.
#include <iostream>
using f32 = float;
int main() {
f32 p1 = 0;
f32 p2 = 0.2;
f32 diff = p2 - p1;
std::cout << "Initial diff: " << diff << '\n';
constexpr auto sr = 48000;
for (auto i = 1; i < sr * 4; ++i) {
p1 += 1.0f;
p2 += 1.0f;
f32 newdiff = p2 - p1;
if (newdiff != diff) {
std::cout << "New diff at sample " << i << ": " << newdiff << '\n';
diff = newdiff;
}
}
}
[moss@mossybox phasortest]$ c++ -o main main.cpp
[moss@mossybox phasortest]$ ./main
Initial diff: 0.2
New diff at sample 1: 0.2
New diff at sample 4: 0.2
New diff at sample 16: 0.200001
New diff at sample 64: 0.199997
New diff at sample 256: 0.200012
New diff at sample 1024: 0.199951
New diff at sample 4096: 0.200195
New diff at sample 16384: 0.199219
New diff at sample 65536: 0.203125
The simplest explanation I can offer is: floating point math is hard and often counterintuitive.
Numerical instability is often going to result from adding and subtracting small and large floating point numbers, and that’s what this code does. You could say that the additions in phasor are just as responsible for the observed behavior as the subtraction in the last line. I would recommend reading https://floating-point-gui.de/ and optionally What Every Computer Scientist Should Know About Floating-Point Arithmetic for more information.
1 Like
Thanks for the explanation and C++ example!
The provided guides are also nice material
When numbers very close to each other are subtracted, the result’s less significant digits consist mostly of rounding errors - the more the closer the original numbers were. As an extreme example, in a single-precision calculation of the form 100,000,000 * (f1() - f2()) + 0,0001 where f1() and f2() are different functions that should return the same value, rounding errors will likely cause f1() - f2() to be (incorrectly) non-zero. Magnified by multiplication with a large value, the final result could be many orders of magnitude bigger than the 0,0001 value it should have.
https://floating-point-gui.de/errors/propagation/