Proposal: SynthDefs could eliminate duplicate UGens

Development
21

Hello,

Here (3.11.2):

LPF.ar.isKindOf(PureUGen) == true
LPF.superclass.superclass == PureUGen

Is the use of a random number generator the only way for a UGen to be non-deterministic?

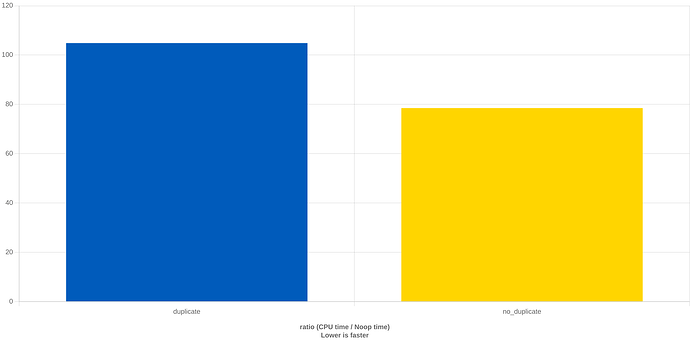
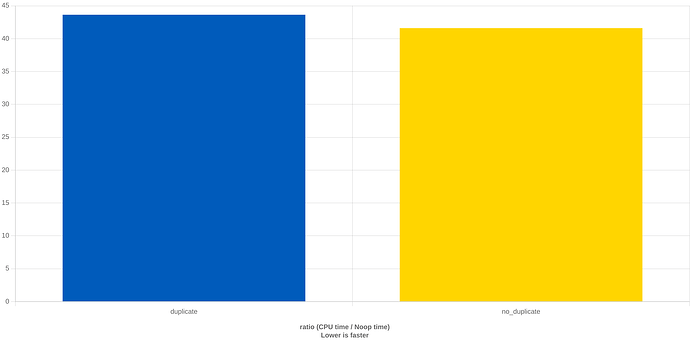
Demand UGens also behave differently if shared, ie.

// Dseq ; shared dseq, different patterns
{var a = Dseq.new(list: [1,3,2,7,8], repeats: inf)
;var t = Impulse.kr(freq: 5, phase: 0)
;var f = Demand.kr(trig: t, reset: 0, demandUGens: [a,a]) * 30 + 340
;SinOsc.ar(freq: f, phase:  0) * 0.1}

// Dseq ; distinct dseq, equal patterns
{var a = Dseq.new(list: [1,3,2,7,8], repeats: inf)
;var b = Dseq.new(list: [1,3,2,7,8], repeats: inf)
;var t = Impulse.kr(freq: 5, phase: 0)
;var f = Demand.kr(trig: t, reset: 0, demandUGens: [a,b]) * 30 + 340
;SinOsc.ar(freq: f, phase:  0) * 0.1}

Best,
Rohan

Ps. Some lists.

Here (3.11.2) the list of UGens marked Pure is:

A2K APF AllpassC AllpassL AllpassN AmpComp AmpCompA BAllPass BBandPass BBandStop BHiPass BHiShelf BLowPass BLowShelf BPF BPZ2 BPeakEQ BRF BRZ2 COsc CombC CombL CombN Decay Decay2 DegreeToKey Delay1 Delay2 DelayC DelayL DelayN DetectIndex DetectSilence FOS Formant Formlet FreeVerb HPF HPZ1 HPZ2 Impulse Index IndexInBetween IndexL Integrator K2A LFCub LFPar LFPulse LFSaw LFTri LPF LPZ1 LPZ2 Lag Lag2 Lag2UD Lag3 Lag3UD LagUD LeakDC LinExp Median MidEQ MoogFF OnePole OneZero Osc OscN RHPF RLPF Ramp Resonz Ringz SOS Select Shaper SinOsc SinOscFB Slew Slope SyncSaw T2A T2K TwoPole TwoZero VOsc VOsc3 VarLag VarSaw Vibrato WrapIndex

(Vibrato is an error, I think. The rateVariation and depthVariation are noise level controls.)

But it’s less work to annotate things the other way about, which I have as:

BrownNoise ClipNoise CoinGate Dbrown Dbufrd Dbufwr Dconst Dgeom Dibrown Diwhite Dpoll Drand Dreset Dseq Dser Dseries Dshuf Dstutter Dswitch Dswitch1 Dunique Dust Dust2 Dwhite Dwrand Dxrand ExpRand Gendy1 Gendy2 Gendy3 GrayNoise IRand LFClipNoise LFDClipNoise LFDNoise0 LFDNoise1 LFDNoise3 LFNoise0 LFNoise1 LFNoise2 LinRand LocalBuf NRand PV_BinScramble PV_RandComb PV_RandWipe PinkNoise Rand TExpRand TIRand TRand TWindex Vibrato WhiteNoise

Which then gives the list of un-annotated Pure UGens as:

Amplitude Balance2 Ball BeatTrack BeatTrack2 BiPanB2 Blip BlockSize BufAllpassC BufAllpassL BufAllpassN BufChannels BufCombC BufCombL BufCombN BufDelayC BufDelayL BufDelayN BufDur BufFrames BufRateScale BufRd BufSampleRate BufSamples BufWr CheckBadValues Clip Compander CompanderD ControlDur ControlRate Convolution Convolution2 Convolution2L Convolution3 Crackle CuspL CuspN DC DecodeB2 DelTapRd DelTapWr Demand DemandEnvGen DiskIn DiskOut Done Duty EnvGen FBSineC FBSineL FBSineN FFT FSinOsc Fold Free FreeSelf FreeSelfWhenDone FreeVerb2 FreqShift GVerb Gate GbmanL GbmanN GrainBuf GrainFM GrainIn GrainSin Hasher HenonC HenonL HenonN Hilbert IEnvGen IFFT In InFeedback InRange InRect InTrig InfoUGenBase KeyState KeyTrack Klang Klank LFGauss LagIn LastValue Latch LatoocarfianC LatoocarfianL LatoocarfianN LeastChange Limiter LinCongC LinCongL LinCongN LinPan2 LinXFade2 Line Linen LocalIn LocalOut Logistic LorenzL Loudness MFCC MantissaMask ModDif MostChange MouseButton MouseX MouseY NodeID Normalizer NumAudioBuses NumBuffers NumControlBuses NumInputBuses NumOutputBuses NumRunningSynths OffsetOut Onsets Out PSinGrain PV_Add PV_BinShift PV_BinWipe PV_BrickWall PV_ConformalMap PV_Conj PV_Copy PV_CopyPhase PV_Diffuser PV_Div PV_HainsworthFoote PV_JensenAndersen PV_LocalMax PV_MagAbove PV_MagBelow PV_MagClip PV_MagDiv PV_MagFreeze PV_MagMul PV_MagNoise PV_MagShift PV_MagSmear PV_MagSquared PV_Max PV_Min PV_Mul PV_PhaseShift PV_PhaseShift270 PV_PhaseShift90 PV_RectComb PV_RectComb2 Pan2 Pan4 PanAz PanB PanB2 PartConv Pause PauseSelf PauseSelfWhenDone Peak PeakFollower Phasor Pitch PitchShift PlayBuf Pluck Poll Pulse PulseCount PulseDivider QuadC QuadL QuadN RadiansPerSample RandID RandSeed RecordBuf ReplaceOut Rotate2 RunningMax RunningMin RunningSum SampleDur SampleRate Sanitize Saw Schmidt SendTrig SetResetFF SpecCentroid SpecFlatness SpecPcile Spring StandardL StandardN Stepper StereoConvolution2L SubsampleOffset Sum3 Sum4 Sweep TBall TDelay TDuty TGrains Timer ToggleFF Trig Trig1 VDiskIn Warp1 Wrap XFade2 XLine XOut ZeroCrossing MaxLocalBufs MulAdd SetBuf

22

Ah… I remembered it incorrectly. I looked at PureUGens a few years ago and I found a lot of them, e.g. Pulse, which AFAICS should be pure but aren’t.

Somehow I thought Filter did not inherit from PureUGen but now I see that was faulty memory.

Notes for the “should-be-pure” list:

  • PV_ units should not be pure because they modify buffer contents.
  • Buf* delays modify buffer contents, as do DiskIn and DiskOut.
  • Chaos and noise units should (probably?) not be pure because they change a random number generator’s state. RandSeed can’t be pure for the same reason.
  • *Out units modify buses.
  • SendReply / SendTrig send OSC.
  • Probably other types of side effects should be considered as well.

IMO PureUGen should be reserved for units that have absolutely no side effects outside of their direct output (and “side effects” should be broadly, liberally considered because it would be very bad if the user expects x and y side effects, but gets only x). Of course UGens in general update their member variables, but member variables are private so that’s not a side effect. Writing to buses or buffers, sending messages, etc are different from that.

For that reason, PureUGen probably is a valid check – even if two “side-effect-y” UGens are behaviorally deterministic and have the same input, if there are two of them, the user expects two side effects, so we can’t drop one.

hjh

23

Hello,

I think the Chaos UGens can be considered similarly to SinOsc, they’re just ordinary equations over their parameters?

Also, I mentioned Pure because it’s nice that it already exists!

But also, it’s not very clear what it means.

The help for Pure says it’s for both “common subexpression elimination” and “dead code elimination”.

In:

{SinOsc.ar(freq: 440, phase: 0) * 0.1
;SinOsc.ar(freq: 220, phase: 0) * 0.1}

the latter happens (very quietly!).

In:

{var a = SinOsc.ar(freq: 220, phase: 0)
;var b = SinOsc.ar(freq: 220, phase: 0)
;(a + b)* 0.05}

the former doesn’t.

In:

{var a = SinOsc.ar(freq: 220, phase: 0) * 0.1
;ReplaceOut.ar(bus: 0, channelsArray: a)
;ReplaceOut.ar(bus: 0, channelsArray: a)}

the latter doesn’t (although the “effect” is “dead”?)

As an aside, I’d be curious about interesting graphs that have multiple “buffer-side-effecting” UGens with equal parameters, if anyone reading has examples?

Where “interesting” is meant to exclude things like:

{var a = SinOsc.ar(freq: 220, phase: 0) * 0.05
;Out.ar(bus: 0, channelsArray: a)
;Out.ar(bus: 0, channelsArray: a)}

Best,
Rohan

24

AFAIK there is no common subexpression elimination logic currently, so the helpfile is … uhm… optimistic :laughing:

I tend to think that a better starting place is not to drop any side effects, even if (as in ReplaceOut) one side effect renders the other moot.

And yes, chaos units without RNGs could be pure. (Should be all of them.)

hjh

25

… wrote the code in the back of a tour bus as the battery ran out on my laptop and just wanted to share something I was working on with another user.

This also underscores: SC is a livecoding tool. A lot of times the goal really is get something out as soon as possible because people on the dance floor want to hear something new. Often there’s no time for elegance or code review.

I think it’s more than just new/inexperienced users who’d benefit from this, and I love the idea of at least getting some metrics on how many real-world SynthDefs would benefit from CSE.

26

A very very quick first step (procrastinating… but really just about 30 minutes).

+ SynthDef {
	checkCSE {
		var units = IdentityDictionary.new;
		var duplicates;
		var lookup;
		children.do { |unit|
			if(unit.isKindOf(PureUGen)) {
				lookup = units[unit.lookupKey];
				if(lookup.isNil) {
					lookup = Dictionary.new
					.put(unit.inputs, unit);
					units.put(unit.lookupKey, lookup);
				} {
					if(lookup[unit.inputs].notNil) {
						duplicates = duplicates.add(unit);
					} {
						lookup.put(unit.inputs, unit);
					};
				}
			}
		};
		duplicates.do { |unit|
			"SynthDef '%' duplicate unit: %(%)"
			.format(name, unit.dumpName,
				unit.inputs.collect { |in|
					if(in.respondsTo(\dumpName)) { in.dumpName } { in }
				}.join(", ")
			)
			.postln;
		};
		^duplicates
	}
}

+ UGen {
	lookupKey { ^this.class.name }
}

+ BasicOpUGen {
	lookupKey { ^operator }
}

Here, I found a catch: BasicOpUGen is not pure! That’s possibly because some of the operators use random number generators. So the test will have to be changed.

But, just for the sake of a proof of concept, change it to BasicOpUGen : PureUGen. Then:

(
SynthDef(\test, {
	var a = SinOsc.ar(freq: 220, phase: 0)
	;var b = SinOsc.ar(freq: 220, phase: 0)
	;var c = a + b
	;Out.ar(0, (a + b) * 0.05)
	;Out.ar(100, c)
}).checkCSE;
)

SynthDef 'test' duplicate unit: 1_SinOsc(220, 0)
SynthDef 'test' duplicate unit: 4_+(0_SinOsc, 1_SinOsc)

That’s not going as far as eliminating the common subexpressions, but it does find them (even with UGens as inputs).

How costly is it? This is my worst case, of a large number of same-class units with different inputs.

(
f = { |n = 100|
	bench {
		d = SynthDef(\additive, {
			var oscs = Array.fill(n, { SinOsc.ar(ExpRand(200, 300)) });
			Out.ar(0, (oscs.sum * 0.001).dup)
		});
	};
	
	bench { d.checkCSE };
};
)

f.(200);
time to run: 0.12884541599988 seconds.
time to run: 0.0033576989999347 seconds.

f.(500);
time to run: 0.56893285199999 seconds.
time to run: 0.0082966729999043 seconds.

f.(1000);
time to run: 2.130532053 seconds.
time to run: 0.014083072999938 seconds.

So… the hash lookup absolutely smokes it (appears to be more or less O(n)).

The final elimination stage would add some cost, but this does suggest that concerns about the performance of a CSE pass were overblown.

hjh