OK I’m sure I’m missing something basic here but I’ve been hammering at this problem for quite a bit.
I have some Pbindef patterns that are similar in functionality to synthesizer modules (they’re sending data to an external source through osc). I have for a example a LFO module that it’s polling volume data.
Each Pbindef is set on an environment variable.
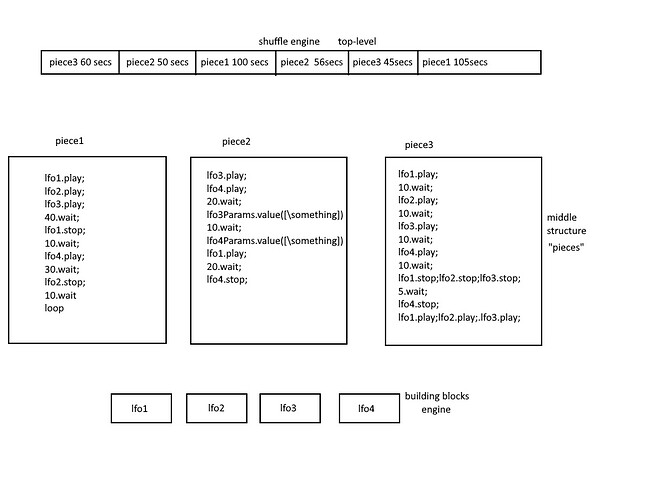
My goal is to be able to organize the way these Patterns are playing and stopping through time, roughly like a music tracker. Each structure will be labeled as a “piece” and then there will be a top level structure shuffling a sequence of the accumulated “pieces”.
I found out two ways to realize this concept but both of them has some issues that I need your help with.
The first way is through Routines, let’s take the following case:
~piece1 = Routine ({
~LFO1.play;
~LFO2.play;
7.wait;
~LFO1.stop;
~LFO2.stop;
~LFO3.play;
})
The problem presented here is that the Routine ~piece1 doesn’t control the patterns inside of the routine, that means that when the top level structure .stops the ~piece1 to start another piece, the ~LFO3 Pbindef will hang. More problems arise if you loop the pattern, you can hopefully see the issue.
The second case is with Pspawner:
~piece1 = Pspawner ({ |sp|
sp.par(~LFO1);
sp.par(~LFO2);
sp.wait(7);
sp.suspend(~LFO1);
sp.suspend(~LFO2);
sp.par(~LFO3);
}).play
This is working well for the most part, when the piece stops all the subpatterns stops as well and it almost does what I want.
The problem presented here is (if I"m understanding correctly), that I have to explicitly save the sp.par wrapper into a variable so I can be able to suspend it (above example does not work). This is too cumbersome for big pieces.
So how can I achieve what I want here? Thank you!
 -
-