This is a Request for Comments (RFC). I’m trying to make it happen on this forum to potentially reach more users. If anyone has comments or thoughts about the format itself, I would suggest making a separate post, to keep this discussion clear.
This discussion started on github: Sweep and Phasor do not wrap properly on inter-sample triggers · Issue #6883 · supercollider/supercollider · GitHub. I will keep this post updated with the state of the discussion as it goes on here on the forum.
The problem
Phasor and Sweep perform linear interpolation to calculate triggers’ subsample offsets, but 1) formulas are wrong and 2) the assumption is incompatible with non-linear signals, e.g. Impulse and LFPulse.
As a result Phasor and Sweep don’t reset precisely when triggered. They are expected to reset to their resetPos (0 for Sweep, and we will use 0 for Phasor too in this post), but they have inaccuracies due to the way they calculate subsample interpolation.
SC defines a trigger as a “transition from non-positive to positive”, that is x[t] is a trigger if x[t-1] <= 0 && x[t] > 0. Continuous signals could have such zero-crossing between samples: imagine a signal that outputs [-1,1,-1,1,...], under the assumption that the signal is linear, we can interpolate and assume the zero crossing happens 0.5 samples before each second sample.
Sweep and Phasor use linear interpolation to estimate inter-sample triggers offset and apply a fraction of their increment. For example, if the increment is 10 and subsample offset is 0.5, they would reset to 5 instead of 0. If subsample offset is 0, they would reset to 10: because the signal zero-crossed 1 sample ago, they have to apply a full increment to the current sample.
This assumption doesn’t hold for Impulse or step-like signals, e.g. [0,1,0,1,...] because the signal is non-linear, but it increments “instantly” from 0 to 1, so the zero crossing happens exactly on the 1 samples (every second sample in the example). Applying linear interpolation would result instead in a subsample offset of 0, i.e. triggers happening on the previous sample (the zeros), and the ugens resetting to 10 instead of 0 (if increment is 10 like in the previous example).
So, linear interpolation is incompatible with impulse or step-like signals. Phasor and Sweep also don’t calculate subsample offset correctly (bugged cpp formula), so the current implementation is wrong for both cases (linear and impulse).
Code examples
Here are some code example to illustrate the situation.
If when running this code the first samples of output look different from the pictures, it’s because of other bugs that got recently fixed on develop.
- Impulse triggers:
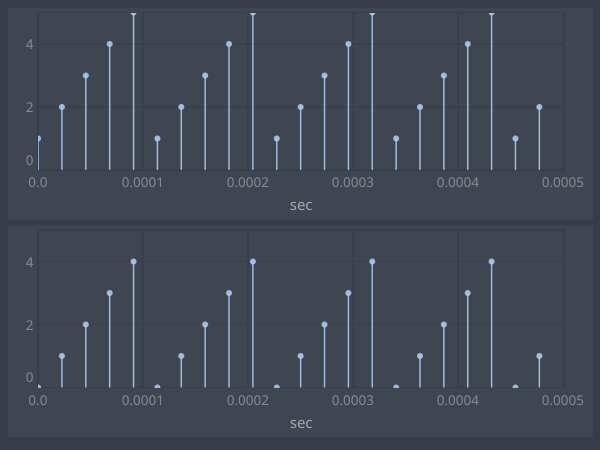
Phasor resets to 1 instead of 0. Sweep looks correct, but only because linear interp formula (cpp) is wrong
{
var trig = Impulse.ar(SampleRate.ir/5);
[Phasor.ar(trig, end: 10), Sweep.ar(trig, SampleRate.ir)]
}.plot(0.0005).plotMode_(\dstems)
- Inter-sample trigger
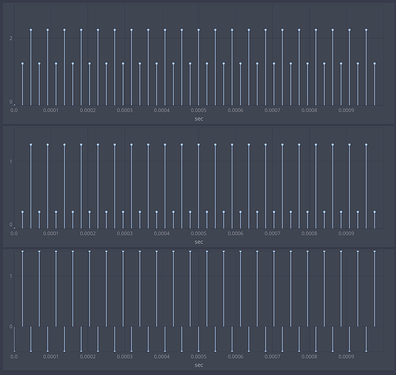
To get triggers between samples, we use a Phasor outputting[-0.5, 1.5, -0.5, 1.5, ...]. This results in a trig on samples 0.25, 2.25, 4.25, etc. That is, every other sample, we would expect UGens to reset to 0 and then apply 0.75 increment, since the inter-sample trig happened 0.75 samples earlier.
Due to errors in the interpolation formula, Sweep resets to 0.25 (= 1 - 0.75) and Phasor to 1.25 (= 1 + 0.25).
(for more details about how the formulas are wrong, see the github issue linked above)
{
var trig = Phasor.ar(0,2,-1,3) + 0.5; // [-0.5, 1.5, -0.5, 1.5, ...]
[
Phasor.ar(trig, 1, 0, 10),
Sweep.ar(trig, SampleRate.ir),
trig
]
}.plot(0.001, separately: true).plotMode_(\dstems)
// output
// Phasor: [0.0, 1.25, 2.25, 1.25, 2.25, 1.25, 2.25, 1.25]
// Sweep: [0.0, 0.25, 1.25, 0.25, 1.25, 0.25, 1.25, 0.25]
// trig: [-0.5, 1.5, -0.5, 1.5, -0.5, 1.5, -0.5, 1.5]
Alternatives for fixing it
We are discussing three alternatives for fixing this behavior. Note that none of these solution is perfectly retro-compatible: we would have in all cases to alter (even if slightly) the output of these UGens. We are talking about changes in the order of sample accuracy, but one never knows how these things amplify when used together in a musical situation.
From the initial discussion on github so far, there was a preference is for option A over the others. On the forum we’ve seen a preference for B, but we’ve found important false positives. Now it seems we are orientating more towards C.
I’m personally biased towards option C. Although I’m trying to be as neutral as possible, I wanted to make this explicit for the reader.
A: add an interp parameter to Sweep and Phasor
Control interpolation explicitly by adding a new interp parameter. It could be set to 0 (no interpolation) by default to support workflow with triggers (arguably the most common), or to 1 (linear interpolation) to maintain the old behavior (although the formula would now be fixed, so it would anyway produce different output).
Pros:
- no new UGens
- predictable behavior, controllable by the user
- works by default with impulses and can be set to interpolate correctly for linear signals
Cons:
- adding a new argument to a UGen is somehow shady: since there is no server-side spec for UGen inputs, the server doesn’t know how many inputs a UGen reads, and it just allocates as many as a SynthDef requests. Unaware clients would make the server allocate one input too few, and the UGens would then read the extra arg from adjacent buffers (likely their own output).
- cpp implementation becomes more complex (more cases to handle)
B: turn off interpolation if x[t-1] == 0.f
This fix attempts to detect impulse and step-like signals by checking if their previous sample was exactly 0, and in this case turn off linear interpolation.
A subsequent improvement proposes to turn on interpolation only if x[t-1] < 0.f || (x[t-1] == 0 && x[t-2] < 0.f). Checking for x[t-2] is proposed to further disambiguate between linear and non linear signals.
if (prevtrig <= 0 && curtrig > 0) {
float offset = 0;
if (prevtrig != 0 || prevprevtrig < 0) {
offset = curtrig / (curtrig - prevtrig) * rate;
}
// apply offset to resetPos
}
@mike @jamshark70 I have tried to be succint here, please let me know if I didn’t represent your proposals properly.
Pros:
- we keep the same UGens and interface: no new UGens, no new parameters
- UGens now behave correctly with impulse triggers, and interpolate correctly for subsample zero-crossings when
x[t-1]< 0 - Other than false positives, changes in UGen outputs would be only fixes: UGens still interpolate, now with the correct offset, including a null offset for Impulses.
Cons:
- Has false positives: linear signals that happen to be exactly 0.f would be treated as impulses (no interpolation). Most prominently, a ramp going
[1.0, 0.0, 0.1]would be treated as an Impulse by all formulas proposed so far. - interpolation can’t be controlled directly by users
C: remove linear interpolation from Sweep and Phasor, and make new dedicated UGens for it (e.g. PhasorL and SweepL)
This fix removes linear interpolation from Sweep and Phasor, and adds new dedicated UGens for it, e.g. SweepL and PhasorL (or Sweep1 and Phasor1).
Pros:
- predictable behavior: Sweep never interpolates and works correctly with triggers, SweepL always interpolates and works correctly with linear continuous signals
- new dedicated UGens could also implement more features for subsample accuracy (e.g. linear interpolation of
rateas well)
Cons:
- adding new UGens for a specialized use case: proliferating UGens may overwhelm users.
- old UGens don’t interpolate anymore, which might “break” old code (old code now produces different output). But apart from their cpp source, these UGens have never “promised” to do interpolation (no mention in schelp docs or code examples), and they have also been doing it wrong for about 20 years without anyone reporting it (to the best of my knowledge).