As long as I’ve been doing this, there are still things I don’t get about filters…
I had thought that a resonant filter with a relatively low Q would have a frequency response more or less similar to LPF.
Not so (with RLPF anyway).
s.boot;
s.freqscope;
(
a = {
var src = PinkNoise.ar(0.1);
var sigs = [src, RLPF.ar(src, 18000, 1), RLPF.ar(src, 18000, 0.5), LPF.ar(src, 18000)];
var x = MouseX.kr(0, sigs.size - 0.01);
// amusing slanted-stairstep interpolation function here
var xFrac = x.frac;
xFrac = clip(wrap(xFrac, -0.5, 0.5) * 10, -0.5, 0.5);
SelectX.ar(
clip(xFrac + (x + 0.5).trunc - 0.5, 0, sigs.size - 0.01),
sigs
).dup
}.play;
)
a.release;
- MouseX band 1 = source (pink noise)
- Band 2 = RLPF at 18000 Hz, Q = 1 (rq = 1): Attenuates quite heavily above 5000 Hz
- Band 3 = RLPF at 18000 Hz, Q = 2 (rq = 0.5): Almost flat response up to 10 kHz
- Band 4 = LPF at 18000 Hz: Similar to 3, but a little less attenuation below 10 kHz
That led me to compare the frequency responses of RLPF and BLowPass.
b = Buffer.alloc(s, 2048, 2);
// record filters' impulse responses
(
a = {
var sig = Impulse.ar(0);
RecordBuf.ar([RLPF.ar(sig, 18000, 1), BLowPass.ar(sig, 18000, 1)],
bufnum: b, loop: 0, doneAction: 2);
Silent.ar(1)
}.play;
)
// get time-domain IRs
b.getToFloatArray(wait: -1, timeout: 5, action: { |data| d = data });
// rejigger into 2 signals
d = d.as(Array).clump(2).flop.collectAs(_.as(Signal), Array);
// get frequency responses
f = d.collect { |ir|
var fft = ir.fft(Signal.newClear(ir.size), Signal.fftCosTable(ir.size)).asPolar;
fft.rho[0 .. ir.size div: 2]
};
// plot FRs
f.lace(f[0].size * 2).plot(numChannels: 2)
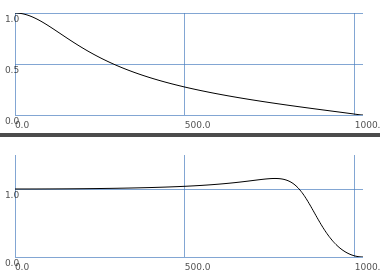
The RLPF frequency response (at the top) is… well… shocking to me. BLowPass is what I would expect for a resonant filter with a high cutoff and low resonance. RLPF… I don’t even know what the [bleep] that is but it was wiping out my drums.
TL;DR is… RLPF might not be doing what you think, while the B*** filters probably are.
hjh