Subdivide phase by Demand sequence and add swing

[dietcv]

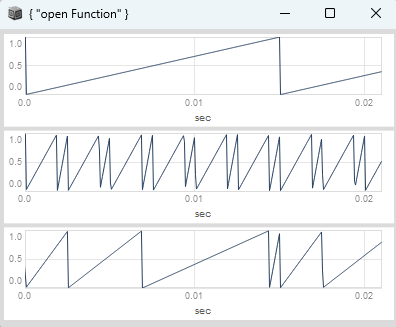
hey, this is a succesor to Subdivide phase by Demand sequence - #6 by dietcv

i have succesfully came up with way to subdivide a measure phase by an arbitrary demand sequence of divisions per measure and to get a continuous event phase.

(
var rampFromBPM = { |bpm, beatsPerMeasure, reset|
	var beatsPerSec = bpm / 60;
	var measureRate = beatsPerSec / beatsPerMeasure;
	var measurePhase = Phasor.ar(reset, measureRate * SampleDur.ir);
	(measurePhase - SampleDur.ir).wrap(0, 1);
};

var rampToTrig = { |phase|
	var history = Delay1.ar(phase);
	var delta = (phase - history);
	var sum = (phase + history);
	var trig = (delta / sum).abs > 0.5;
	Trig1.ar(trig, SampleDur.ir);
};

var rampToSwing = { |measurePhase, stepsPerMeasure, swing|
	var swingCount = stepsPerMeasure / 2;
	var swingPhase = (measurePhase * swingCount).wrap(0, 1);
	var swingIndex = (measurePhase * swingCount).floor;	
	var swingPhaseShaped = swingPhase.linlin(0, 1, swing.neg, 1 - swing).bilin(0, swing.neg, 1 - swing, 0.5, 0, 1);
	swingIndex + swingPhaseShaped / swingCount;
};

var rampToSlope = { |phase|
	var history = Delay1.ar(phase);
	var delta = (phase - history);
	delta.wrap(-0.5, 0.5);
};

var accum = { |trig|
	Duty.ar(SampleDur.ir, trig, Dseries(0, 1));
};

{
	var measurePhase, measurePhaseSwing, stepPhase, stepTrigger, stepSlope;
	var stepIndex, eventTrigger, eventPhase, eventDuration, stepDuration;

	var plotScale = 100;
	var stepsPerMeasure = 12;

	// measure phase
	measurePhase = rampFromBPM.(\bpm.kr(160) * plotScale, \beatsPerMeasure.kr(4), \reset.tr(0));
	measurePhaseSwing = rampToSwing.(measurePhase, stepsPerMeasure, \swing.ar(0.5));

	// step phase, slope, trigger and duration
	stepPhase = (measurePhaseSwing * stepsPerMeasure).wrap(0, 1);
	stepSlope = rampToSlope.(stepPhase);
	stepTrigger = rampToTrig.(stepPhase);
	stepDuration = rampToSlope.(measurePhase) / rampToSlope.(measurePhaseSwing);

	eventDuration = Ddup(2, Dseq([2, 6, 1, 2, 1], inf));
	eventDuration = Demand.ar(stepTrigger, 0, Ddup(eventDuration, eventDuration));

	stepIndex = Demand.ar(stepTrigger, 0, Dseq([Dseries(0, 1, eventDuration)], inf));

	eventTrigger = stepTrigger * Demand.ar(stepTrigger, 0, Dswitch1([1] ++ (0 ! (stepsPerMeasure - 1)), stepIndex));

	eventPhase = stepSlope * stepDuration / eventDuration * accum.(eventTrigger);

	[measurePhase, stepPhase, eventPhase];
}.plot(0.021);
)

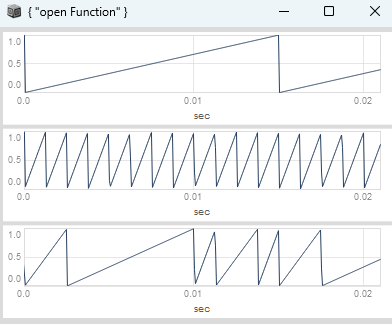
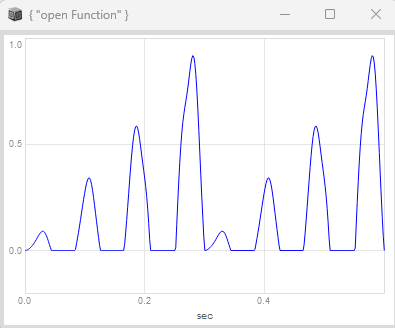
now i would like to add my rampToSwing function, its swinging every other step and adjust the event phase accordingly:

here swing is set to 0.75:

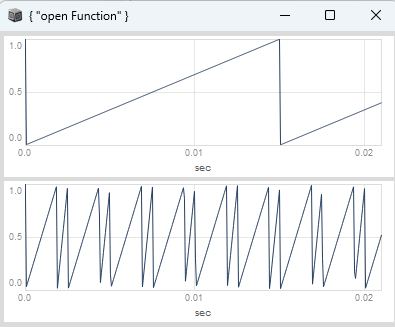
you can calculate the swung step duration by the slope of the measure phase divided by the slope of the swung measure phase. when setting swing to 0.75 you get a sequence for the step duration of 1.5, 0.5, 1.5, 0.5, etc.

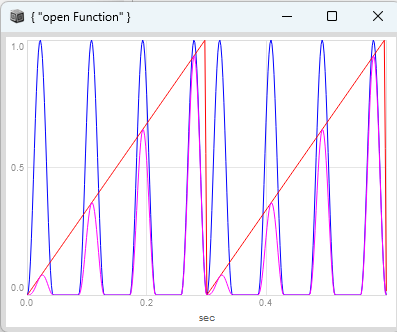
I have tried to use the stepDuration to scale the step slope to get a continous event phase between 0 and 1:

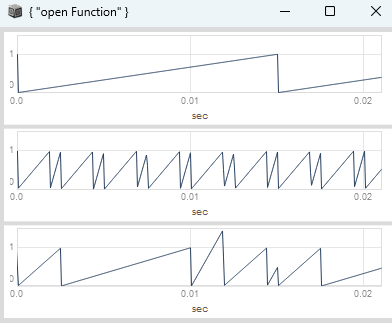
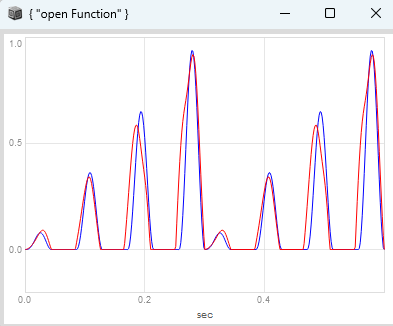
the event phase is continuous but as you can see in the plot, the problem arises for odd durations. for a sequence of event durations of [2, 6, 1, 2, 1] only the odd numbers, in this case the duration of 1 causes the event slope to be either outside of the range of 0 to 1 or not reach 1 at all, depending on its index in the sequence of durations.

I know that this is tricky but maybe someone is interested helping me out

[dietcv]

This part of the code is a hacky solution which repeats every item in the array x for x times on every step trigger and therefore gives the event duration, which is then used to run a counter to output a trigger for every new event, which is then used to reset the accumulator per event to get the event phase:

eventDuration = Ddup(2, Dseq([2, 6, 1, 2, 1], inf));
eventDuration = Demand.ar(stepTrigger, 0, Ddup(eventDuration, eventDuration));

stepIndex = Demand.ar(stepTrigger, 0, Dseq([Dseries(0, 1, eventDuration)], inf));

eventTrigger = stepTrigger * Demand.ar(stepTrigger, 0, Dswitch1([1] ++ (0 ! (stepsPerMeasure - 1)), stepIndex));

[dietcv]

Ive figured out an overcomplicated way which is not quite universal yet, because of the slope calculaton with Slope.ar or (phase - Delta1.ar(phase)). If you use a hardcoded Demand sequence of alternating values between \swing.kr * 2 and (1 - (\swing.kr * 2)).abs it works fine. In gen~ i get precise values of 1.5 and 0.5 for the stepDuration calculated by the slope instead of jittering floats.

(
var rampFromBPM = { |bpm, beatsPerMeasure, reset|
	var beatsPerSec = bpm / 60;
	var measureRate = beatsPerSec / beatsPerMeasure;
	var measurePhase = Phasor.ar(reset, measureRate * SampleDur.ir);
	(measurePhase - SampleDur.ir).wrap(0, 1);
};

var rampToTrig = { |phase|
	var history = Delay1.ar(phase);
	var delta = (phase - history);
	var sum = (phase + history);
	var trig = (delta / sum).abs > 0.5;
	Trig1.ar(trig, SampleDur.ir);
};

var rampToSwing = { |measurePhase, stepsPerMeasure, swing|
	var swingCount = stepsPerMeasure / 2;
	var swingPhase = (measurePhase * swingCount).wrap(0, 1);
	var swingIndex = (measurePhase * swingCount).floor;
	var swingPhaseShaped = swingPhase.linlin(0, 1, swing.neg, 1 - swing).bilin(0, swing.neg, 1 - swing, 0.5, 0, 1);
	swingIndex + swingPhaseShaped / swingCount;
};

var rampToSlope = { |phase|
	var history = Delay1.ar(phase);
	var delta = (phase - history);
	delta.wrap(-0.5, 0.5);
};

var accum = { |trig|
	Duty.ar(SampleDur.ir, trig, Dseries(0, 1));
};

{
	var measurePhase, measurePhaseSwing, stepPhase, stepTrigger, stepSlope;
	var stepIndex, eventTrigger, eventPhase, eventDuration, stepDuration;
	var stepPhaseSwing, stepSlopeSwing;

	var plotScale = 100;
	var stepsPerMeasure = 12;

	// measure phase
	measurePhase = rampFromBPM.(\bpm.kr(160) * plotScale, \beatsPerMeasure.kr(4), \reset.tr(0));
	measurePhaseSwing = rampToSwing.(measurePhase, stepsPerMeasure, \swing.kr(0.75));

	// step phase, slope, trigger and duration
	stepPhase = (measurePhase * stepsPerMeasure).wrap(0, 1);
	stepPhaseSwing = (measurePhaseSwing * stepsPerMeasure).wrap(0, 1);

	stepSlope = rampToSlope.(stepPhase);
	stepSlopeSwing = rampToSlope.(stepPhaseSwing);

	stepTrigger = rampToTrig.(stepPhaseSwing);
	//stepDuration = rampToSlope.(measurePhase) / rampToSlope.(measurePhaseSwing);
	stepDuration = Demand.ar(stepTrigger, 0, Dseq([\swing.kr * 2, (1 - (\swing.kr * 2)).abs], inf));
	//stepDuration = Demand.ar(stepTrigger, 0, Dseq([(1 - (\swing.kr * 2)).abs, \swing.kr * 2], inf));

	eventDuration = Ddup(2, Dseq([2, 3, 6, 1], inf));
	eventDuration = Demand.ar(stepTrigger, 0, Ddup(eventDuration, eventDuration));

	stepIndex = Demand.ar(stepTrigger, 0, Dseq([Dseries(0, 1, eventDuration)], inf));

	eventTrigger = stepTrigger * Demand.ar(stepTrigger, 0, Dswitch1([1] ++ (0 ! (stepsPerMeasure - 1)), stepIndex));

	// if duration is even select duration else select scaled duration
	// if duration is odd and starts on "longer" step add (1 - (swing * 2)) else subtract (1 - (swing * 2))
	eventPhase = stepSlope / Select.ar(eventDuration % 2, [
		eventDuration,
		eventDuration + ((1 - (\swing.kr * 2)) * Select.ar(Latch.ar(stepDuration, eventTrigger) > (1 - (\swing.kr * 2)).abs, [K2A.ar(1), K2A.ar(-1)]))
	]) * accum.(eventTrigger);

	[measurePhase, stepPhaseSwing, eventPhase];
}.plot(0.021);
)

[QQQQ]

Just wanted to say how much I appreciate you sharing this (and your other in-progress work)—thank you!

[mousaique]

hi @dietcv,

i’m not quite sure yet i fully grasp your example, but is it in effect a potential solution to this matter discussed a few weeks ago? Resetting start count with PulseDivider? - #30 by dietcv - namely asynchronous overlapping grains?
If so, this demands the asynchronous sequence to be hardcoded so as to be predictable?

Thanks
Jan

[dietcv]

hey,

its unfortunately not solving anything related to this thread. The solution i have suggested there is still the best i could come up with. But im currently working on a pulsar / grain Ugen in gen which has no problems with multichannel expansion (asynchronous overlapping grains or sequencing of events at audio rate) and is capable of heavy modulation per grain (cross feedback FM) and anti-aliased which i will export to SC.
Im currently just trying to get more possibilites out of audio rate sequencing and figuring out some interesting design decisions for sequencing granular events. It turns out that SC is really nice for prototyping using some plots.
Im currently working on an audio rate sequencing suite in gen which will be exported as Ugens to SC with some of my approaches

really cool to see you @mousaique @QQQQ participating. It currently seems to be a rather unpopular topic in SC. But i just keep posting my stuff Probably better to start a blog.

[mousaique]

i see! nevertheless, your outlined Ugen sounds really promising can’t wait to see it happening!!
i believe maybe the threshold to actively participate in these threads might be quite challenging also due to the complexity of the examples, i assume that eventually it will find its readership;) but a blog also surely good and fitting format as research notebook. good luck with all the further experimenting!!

[dietcv]

@mousaique @QQQQ would you be more interested in buffered waveforms + buffered grain envelopes / windows or stateless modulatable window functions + sinusoidal carrier waveforms? Could you tell me about your specific use cases ? With my experiments I found out that the higher the trigger rate, the more the window shape contributes to the overall sound and the carrier waveform itself isn’t that important. So my idea is to have cross feedback fm with sinusoids and additional onepole filters in the feedback path to shape the modulation and an additional modulatable function for the frequency trajectory per grain and a modulatable tilted tukey window for the grain window (that’s already working, currently just trying to figure out the anti-Aliasing and make some design decisions) But everything else is also possible.

I also found out that its desirable to have modulatable shapes on a micro scale per grain and additional modulation on a macro scale of the same params. These additional modulations would be no problem to implement directly in SC then with subdividing a phase for different modulation rates.
But thats where some of my sequencing ideas could come into play. Still working on a universal shift register with a self modulating feedback path for chaotic behaviour for modulation.

[QQQQ]

I most work with pulsar synthesis, buffered waveforms (with BufRd) and grain envelopes and per-grain FM with buffered waveforms (Frequency instead of phase - #29 by dietcv). The modulations you mention in your second paragraph sound great—definitely interested in that. And I’d be curious about FM with sinusoidal carriers and modulatable windows, too.

[mousaique]

hi @dietcv ,
that all sounds pretty great!!
i generally work with buffered waveforms, also to be able to use long recordings as source material (i don’t really use one-cycle pulsarets often). i do find the area between original timbre and its increasing synthetic feel through different granular approaches very interesting to explore. but i do value the option of having an external timbral blueprint on the material. as for the windowing this modulatable tukey window already covers a lot of ground. and actually granular feedback is a relatively unexplored area yet for me, so i’d be very curious on those implementations!..
thanks so much for the research!

[dietcv]

@QQQQ are you creating or using different buffered single cycles / envelope shapes or mostly the same?
Im asking because over a year i have made a lot of pulsar patches with buffered single cycles and envelope shapes and after that i looked at all the patches and evaluated how often i used which single cycles or envelope shapes. It turned out that most of the time the shapes have been more basic then i thought and mostly the same. For that reason i think its more interesting to start with basic shapes and have some modulation capabilities for different timbres then start with static complex single cycles or envelope shapes. Could you share some of the shapes you are using?

@mousaique thanks for your reply I also think that the modulatable tukey window covers alot of ground. It gives you hanning, square, percussive and reversed percussive shapes per grain (modulatable tilt and width params) and should be accompanied with an additional envelope which has a longer duration (for example one measure) and max 2 shaping params as well. I think getting complex modulation out of basic ingredients is better then having a static complex modulation source which cant be changed at all.

[QQQQ]

@dietcv, for the pulsarets, I probably use about 20 different buffered, single-cycle waveforms—different variations of sinusoidal, more or less saw-shaped, and square waveforms—to get different kinds of transients. For the envelopes, I also use about 20 waveforms, mostly various bell- and percussive shapes, some are more complex for a ring-modulation-like effect. I’ve tried additional shapes, but, as you wrote earlier, the differences are often not that significant. Does that answer your question? Happy to write more if that’s helpful.

[dietcv]

hey, thanks for letting me know I think your discoveries match with what i found out. It would be cool to have plots of all the shapes you are using. Im trying to generalize some interesting shaping functions to get more complex pulsaret shapes from basic sin functions and envelopes with just a few control params.

For example cubic interpolation:

(
var cubicInterpolation = { |x, control|
	var a = control.neg;
	var d = control;
	(x * (1 - (((2 * a) + d) / 6))) +
	((x * x) * ((a + 1) / 2)) +
	((x * x * x) * (((-1) / 2) + ((d - a) / 6)))
};

{
	var phase = Phasor.ar(0, 220 * SampleDur.ir);
	var interp = cubicInterpolation.(phase, MouseX.kr(0, 200).poll);
	var sine = sin(interp * 2pi);
	sine!2 * 0.1;
}.play;
)

I have played around with the shapes from the nuPG for some time now which are all from a single cycle pack by christian vogel which is now offline.
This pack seems to be the “go to buffered single cycle pack” for all the pulsar people independent from the implementation they are using (probably because of the nuPG). But alot of the more complex single cycle shapes you could use as pulsarets just sound like noise and introduce heavy aliasing. So i think basic shapes with modulation capabilities are more interesting then static complex shapes, especially if you use oversampling / bandlimiting.

One example for complex envelopes:
One of the envelope shapes from the pack i was using was this one, which i used as a grain window (i was just trying out all the shapes without thinking about it, and this one sounded cool):

If you apply these more complex envelope shapes you get instantly interesting results, but the downside is you are stuck then with what you have without the possibility for variation.

You could for example recreate this one by noticing that its basically a trigger mask sequence of 7 steps [1, 0, 1, 0, 1, 0, 1]
and two shapes, one hanning window shape on the micro scale per grain and one linear shape on the macro scale and the trigger frequency ratio between them is 7.

blue = hanning micro scale, red = linear macro scale and pink the resulting shape:

here is comparision with the buffered complex shape (red) and the resulting shape (blue):

[wehrk]

@dietcv

Probably better to start a blog.

I’m def in to follow your blog if it will pop up one day! Many of your posts on this forum have been the most useful for me

[asher]

Hey there, I’ve been following your threads - I’ve worked in gen for a very long time but not as long in SC - do you have a reliable method/template of exporting ~gen to ugen you’d be willing to share?

[dietcv]

Cool. Im currently getting familiar with RNBO.

Supercollider UGen Starter

[dietcv]

thanks a lot for the kind words