hey,
im trying to build a “time-varying” Feedback Delay Network (FDN).
For that to work i would like to change the delay weights of the feedback matrix by modulating the angle of the matrix with a control signal (LFO or Envelope) to rotate it by that angle in real time.
This idea of modulating the delay weights of the feedback matrix is loosely based on the “ZIGZAG” max4live device and results in a very interesting “swooshing” effect.
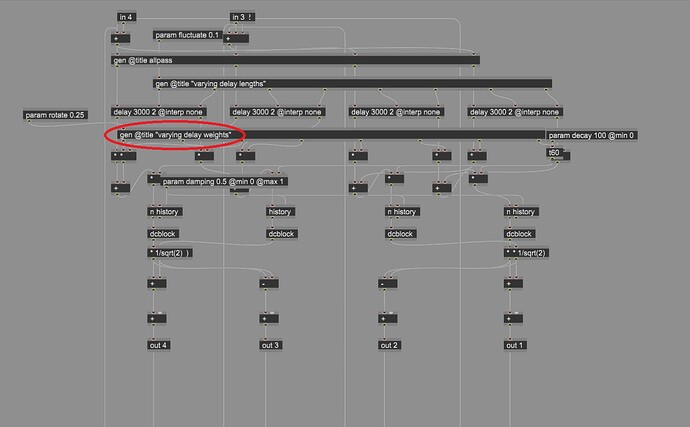
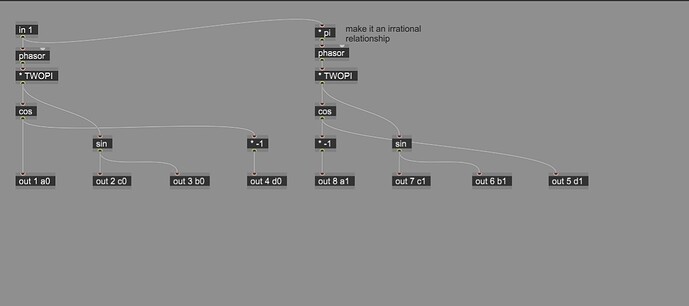
Ive made a rough sketch to create a rotatable feedback matrix by taking the kronecker product of the 2x2 givens rotation and a 4x4 householder reflection.
How can i now use a control signal to modulate the angle of the feedback matrix?
any other ideas ? thanks 
(
var s, c, angle;
// modulation of angle inside SynthDef with LFO?
angle = 0;
s = angle.sin;
c = angle.cos;
~givens2x2 = [
[c, s.neg],
[s, c]
];
~householder4x4 = [
[-0.5, 0.5, 0.5, 0.5],
[ 0.5,-0.5, 0.5, 0.5],
[ 0.5, 0.5,-0.5, 0.5],
[ 0.5, 0.5, 0.5,-0.5],
];
~kronecker = { |a, b|
a.collect { |x|
x.collect { |y| b * y }.reduce('+++')
}.reduce('++')
};
~circulant_fb_matrix = ~kronecker.(~givens2x2, ~householder4x4);
)
i already have this “non-time varying” FDN based on a hadamard 8x8 feedback matrix + reflector working and would like to implement the modulation of the delay weights here. You can have a listen below:
(
var matrix;
matrix = [
[ 1, 1, 1, 1, 1, 1, 1, 1 ],
[ 1, -1, 1, -1, 1, -1, 1, -1 ],
[ 1, 1, -1, -1, 1, 1, -1, -1 ],
[ 1, -1, -1, 1, 1, -1, -1, 1 ],
[ 1, 1, 1, 1, -1, -1, -1, -1 ],
[ 1, -1, 1, -1, -1, 1, -1, 1 ],
[ 1, 1, -1, -1, -1, -1, 1, 1 ],
[ 1, -1, -1, 1, -1, 1, 1, -1 ],
] * ( sqrt(2).reciprocal * sqrt(2).reciprocal * sqrt(2).reciprocal );
SynthDef(\jot_stereo, {
var ffreq = \ffreq.kr(16000);
var fq = \fq.kr(0.5);
var feedback = \feedback.kr(-3);
var sampleRate = 44100;
var sig, inSig, localOut;
var reverbTime, decayCoef, delTimesSec, delTimes, order;
var decayScale = \decayScale.kr(0.05);
order = matrix.size;
delTimes = order.collect({|i| rrand(1000, 4599).nextPrime });
( delTimes / sampleRate ).debug(\delTimes_);
( delTimes.sum / sampleRate ).debug(\delTimes_sum_);
inSig = In.ar(\in.kr(0), order);
inSig.collect { |it| it.source}.debug(\input);
sig = inSig + LocalIn.ar(order);
// multiplying signals by matrix
sig = matrix.collect({|it i| matrix[i].collect({|item j| item * sig[j] }).sum });
delTimesSec = delTimes / sampleRate;
reverbTime = \reverbTime.kr(1).lag(2);
decayCoef = 0.001.pow(delTimesSec * decayScale / reverbTime);
localOut = order.collect({|i|
DelayN.ar(sig[i], delTimesSec[i], delTimesSec[i] * decayScale - ControlDur.ir);
});
localOut = order.collect({|i|
HighShelf.ar(localOut[i], ffreq, fq, feedback) * decayCoef[i];
});
LocalOut.ar(localOut);
sig = localOut.size.div(2).collect({|i|
i = i * 2;
[
localOut[i] * -1,
localOut[i + 1]
]
}).sum;
sig = HighShelf.ar(sig, ffreq, fq, feedback.neg);
sig = sig * sqrt(reverbTime).reciprocal;
sig = LeakDC.ar(sig);
//sig = SafetyLimiter.ar(sig);
Out.ar(\out.kr(0), sig);
}).add;
SynthDef(\reflector, {
var numReflcs = 5;
var delays, delayPans, reflections, pannedReflections;
var sig, inSig;
inSig = In.ar(\in.kr(0));
delays = Array.fill( numReflcs, { |i| Rand(0.01, 0.025) });
delays = delays * \scaleDelays.kr(1);
delayPans = Array.fill(numReflcs, { |i|
( \reflPan.kr(0) + ( \spread.kr(1) * [ -1.0, 1.0 ].at(i.mod(2)) ) ).clip2(1)
});
sig = HPF.ar(inSig, \hpfRefl.kr(110));
reflections = Array.fill( numReflcs,
{|i|
DelayN.ar(
OnePole.ar(sig, \lpfRefl.kr(0.9) * Rand(0.8,1)) * Rand(-1,1),
0.2,
delays.at(i)
)
}
);
reflections.do { |it i|
var dt0 = Rand( 0.001, 0.01 );
var dt1 = Rand( 0.001, 0.01 );
reflections[i] = AllpassN.ar(reflections[i], dt0, dt0, Rand(0.1,0.4));
reflections[i] = AllpassN.ar(reflections[i], dt1, dt1, Rand(0.1,0.4));
};
pannedReflections = Array.fill(numReflcs,
{|i|
Pan2.ar(reflections.at(i), delayPans.at(i))
}
);
Out.ar(\out.kr(0), pannedReflections.sum * \amp.kr(0.5));
Out.ar(\fxOut.kr(2), reflections);
}).add;
SynthDef(\chirp, {
var sig, env;
env = EnvGen.ar(Env.perc(0.001, 0.2), doneAction: Done.freeSelf);
sig = Saw.ar(XLine.kr(100, 1000, 0.1));
sig = sig * env;
sig = Pan2.ar(sig, \pan.kr(0), \amp.kr(0.5));
Out.ar(\out.kr(0), sig);
}).add;
)
(
~makeBusses = {
~bus = Dictionary.new;
~bus.add(\reflector -> Array.fill(3, { Bus.audio(s, 1) }));
~bus.add(\tank -> Bus.audio(s, 16));
};
~makeBusses.();
)
(
~mainGrp = Group.new;
~reflectorGrp = Group.after(~mainGrp);
~tankGrp = Group.after(~reflectorGrp);
{
Pdef(\chirp,
Pbind(
\instrument, \chirp,
\freq, 440,
\dur, 1,
\out, ~bus[\reflector][0],
\group, ~mainGrp,
);
).play;
~reflector = Synth(\reflector,
[
\in, ~bus[\reflector],
\lpfRefl, 0.4,
\hpfRefl, 210,
\reflPan, 0,
\spread, 1,
\scaleDelays, 0.05,
\amp, 0.2,
\out, 0,
\fxOut, ~bus[\tank],
],
~reflectorGrp
);
~tank = Synth(\jot_stereo,
[
\in, ~bus[\tank],
\ffreq, 16000,
\fq, 0.8,
\feedback, -15,
\reverbTime, 1,
\decayScale, 0.05,
\out, 0,
],
~tankGrp
);
}.fork
)