Trying to understand reverb signal flow diagrams

Questions Code Review
1

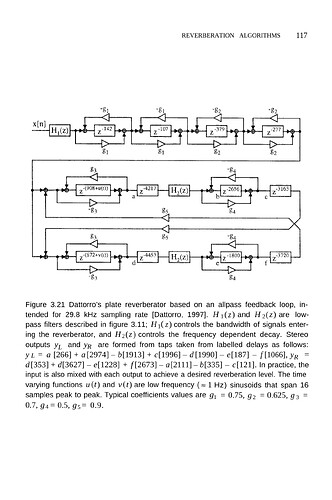
Hi, I’m trying to get a bit more into reverb theory and have been copying a few old algorithms from papers. I’m struggling now with a slightly more complex algorithm and hoping someone here could help me out.

Here’s the algorithm:

dattorro
dattorro1395×2095 294 KB

And here’s my attempt to code it - I have a feeling there might be a few pretty basic mistakes in there!

(
SynthDef(\test, {
        var sig = Saw.ar(XLine.kr(1000, 100, 1) + [0, 1]) * Env.perc(0.01, 1).ar(Done.freeSelf);
        sig = sig * -20.dbamp;
        Out.ar(0, sig);
}).add;

SynthDef(\dattorro, {
        var fb;
        var input = In.ar(0, 2);
        var sum = 0;
        var allpassTimes = [142, 107, 379, 277] / 29800;
        var lfo = 2.collect { SinOsc.kr(rand(0.99, 1.01)) * 16/29800 };
        var sig = LPF.ar(input, 8000);

        // 4 Allpass in series
        4.do { |i|
                sig = AllpassC.ar(sig, 1, allpassTimes[i], 1);
        };

        // fb loop starts here
        fb = sig + LocalIn.ar(2);
        fb[0] = AllpassC.ar(fb[1], 1, 908/29800 + lfo[0]);
        fb[0] = CombC.ar(fb[0], 1, 4127/29800);
        fb[0] = LPF.ar(fb[0], 8000);
        fb[0] = AllpassC.ar(fb[0], 1, 2656/29800);
        fb[0] = CombC.ar(fb[0], 1, 3163/29800);

        fb[1] = AllpassC.ar(fb[0], 1, 672/29800 + lfo[1]);
        fb[1] = CombC.ar(fb[1], 1, 4453/29800);
        fb[1] = LPF.ar(fb[1], 8000);
        fb[1] = AllpassC.ar(fb[1], 1, 1800/29800);
        fb[1] = CombC.ar(fb[1], 1, 3720/29800);
 
        LocalOut.ar(fb);
        sig = input + (fb * -80.dbamp);
        //sig = sig * \amp.kr(-80.dbamp);
        ReplaceOut.ar(0, sig);
}).add;
)

x = Synth.tail(nil, \dattorro);
Synth(\test);

Cheers,
Jordan

1 Like
2

Did you watch: Reververation(10)

His code is in the description.

Sam

1 Like
3

Thanks Sam, this is fantastic.

4

I spot a mistake, CombC should be DelayN. z^-N is the transfer function of an ordinary delay line, not a comb filter. (Comb filters have a very spiky response, algorithmic reverb designers have traditionally avoided that.)

A smaller mistake is that “decayTime” is not set on the allpasses, defaulting to 1.0. SuperCollider uses “decayTime” instead of the feedback coefficient (which is weird, but I guess the code for Allpass was just copied from CombC). The help file has a formula for converting between them.

1 Like