Understanding Resonz

[andie]

I’m trying to wrap my head around the specifics of Resonz.

The paper linked in the help file concludes that the filter should have constant gain with respect to frequency; but I believe this would mean keeping bw constant, which means supercollider’s parameter bwr would have to move in inverse proportion to freq, in order to keep bw and therefore gain constant.

I’m finding the documentation a little thin. Maybe I’m missing something. The .cpp code is also uncommented. I’ve been looking at pages with all these equations but unfortunately that’s not my forte. Wherever I start reading they seem to have defined some of the variables on a previous page and I’m not ready to dig into a textbook from page one… All I’m trying to do is plot freq vs magnitude response given (constant) params freq and bw! Anyone have a good grasp of this stuff?

[andie]

Wow Nathan, that’s amazingly helpful and detailed. I’m very grateful!

Should the ffreq in the second code-block be theta?

The H(z) equation was derived from the code? Or that’s a textbook formula for this kind of filter? I didn’t see the H(z) equation on the “Direct Form II” link, and it’s not clear to me how we know that the Resonz filter implements “Direct Form II”, since the y(t) equation looks to be different.

---

To make things a little more interesting: I noticed that csound also has a resonz, which has more extensive documentation, but which may or may not be the same as our Resonz. Digging into their doc, I found that Stiglitz defines the H(z) equation for csound-Resonz as (1 - z^-2) / (1 - 2Rcos(theta)z^-1 + R^2z^-2).

I subbed this into your python code and noticed that it doesn’t give the same curves as your H, and that the curves do NOT have constant gain.

H = (1 - z2) / (1 - (2 * R * np.cos(theta) * z1) + (R * R * z2))

HOWEVER, when I changed rq to vary with filter_frequency, so as to preserve constant bw, the curves then had constant gain.

plot_resonz_magnitude_response(filter_frequency, rq=(10 / filter_frequency))

So your equation for Resonz has constant gain with constant rq, wheras csound-Resonz has constant gain with constant bw.

If my arithmetic scribblings are correct, though, rq would be more musically useful because it scales the bandwidth to something more like (but not exactly like) the pitch relation rather than the frequency relation.

The curves for csound-Resonz also seem to be taller on the magnitude axis, but I’m not sure whether this is significant.

[andie]

… I’m rethinking the statement that constant rq is necesarily more musically useful than constant bw…

say we have input ideal white noise, and we want to keep output amp constant while moving the frequency, then we need to keep the integral constant, i.e. the area under the peak, not the peak height. so maybe a set of curves more like the csound-Resonz ones is better for that?

Looking at Ringz, I see it says it is like Resonz with “constant skirt” rather than constant gain – perhaps that’s the same as csound-Resonz? Does “constant skirt” imply constant amplitude output as in the ideal example above?

Of course, Ringz does not specify bw or rq, but rather decaytime – the doc says decaytime specifies bandwidth but doesn’t mention exactly how. I’m sure a little dive into the .cpp will turn this relation up without too much trouble, which I will do later and post it here (and I imagine it should be added to the doc as well…)

[alln4tural]

@nathan

the results at least look correct.

and so pretty!

.
.
.

[andie]

You’re right, I’m missing the gain factor – I was looking in the textbook, not the article.

Aside from the gain factor, there is another slight difference in the equations between Stieglitz’ book and article. The book has numerator 1 - z^-2 while the article has 1 - Rz^-2. This doesn’t seem to have to do with the gain factor, and seems to have very little difference on the shape of the curves. Neither one of these quite seems identical to the equation you’ve given, but again, there is no(?) difference in the curves.

Once I added the gain factor in, csound-resonz seems to be the same as our resonz.

[andie]

The only differences I can see between the code of Resonz and Ringz are as follows:

Ringz has R = exp(log001 / (decayTime * SAMPLERATE)
Resonz R = 1 - B * 0.5 [ B is bandwidth ]

Ringz has a0 = 0.5
Resonz a0 = (1 - R2) * 0.5 [ this is the scaling factor ]

modifying the python code to plot it:

import numpy as np
import matplotlib.pyplot as plt

sample_rate = 48000

def plot_ringz_magnitude_response(filter_frequency, decay_time):
    theta = filter_frequency * 2 * np.pi / sample_rate
    #R = 1 - (theta * rq) / 2 #resonz version
    R = np.exp(np.log(0.001) / (decay_time * sample_rate))
    b1 = (4 * R * R * np.cos(theta)) / (1 + R * R)
    b2 = -R * R;
    #a0 = (1 - R * R) / 2 # resonz version
    a0 = 0.5
    A0 = 1
    A1 = -b1
    A2 = -b2
    B0 = a0
    B1 = 0
    B2 = -a0

    frequency = np.linspace(0, sample_rate / 2, 50000)
    omega = frequency * 2 * np.pi / sample_rate
    z = np.exp(omega * 1j)
    z1 = 1 / z
    z2 = 1 / (z * z)
    H = (B0 + B1 * z1 + B2 * z2) / (A0 + A1 * z1 + A2 * z2)
    G = np.abs(H)

    plt.plot(frequency, 20 * np.log10(G))

plt.ylim(-60, 100)
plt.xlabel("Frequency (Hz)")
plt.ylabel("Magnitude (dB)")

for filter_frequency in np.linspace(100, 10000, 10):
    plot_ringz_magnitude_response(filter_frequency, decay_time=1)

plt.savefig("ringz.png")

We can see gains are high and equal, bandwidths are equal. changing decay_time to something very small makes the bandwidth wider and the gain lower.

[andie]

If anyone can work out the relation between bandwidth and decay_time, i’d find that interesting…

[andie]

OK, wow. Thanks very much for that, Nathan. I’m a little over my head with this right now, unfortunately. I’m going to have to step back quite a few steps to understand this kind of stuff. I appreciate a lot that you seem to be up for discussing these issues, and I hope to take you up on it more in the future

Personally it looks like I have to follow two tracks, one to really understand the meaning of the math and how dsp really works, and the other just to use these things programatically with a good understanding of what’s going to happen. Thinking of the Resonz filter as a black-box function, seems to me like there’s a gap where either it must be used “by hand” or really understood on an engineering level. As someone who wants to program with it, I was expecting it to behave like a code library (and be documented like one), and found it a rather odd beast. I’m horrified and fascinated…

---

Ok, back to some details:

I think that where Ringz and Resonz are concerned, to compute the relationship between ringtime and bandwidth, we can use the approximate definition for bandwidth as defined in the code Resonz, and get

R = 1 - B/2 and R = e^(log001 / (decaytime * samplerate))

… so the relationship is dependent on samplerate, but if we solve for rq instead of B then it’s dependent on freq but not samplerate…

---

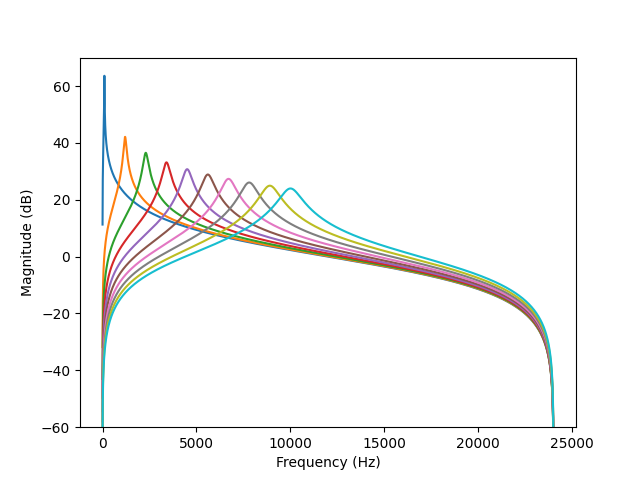
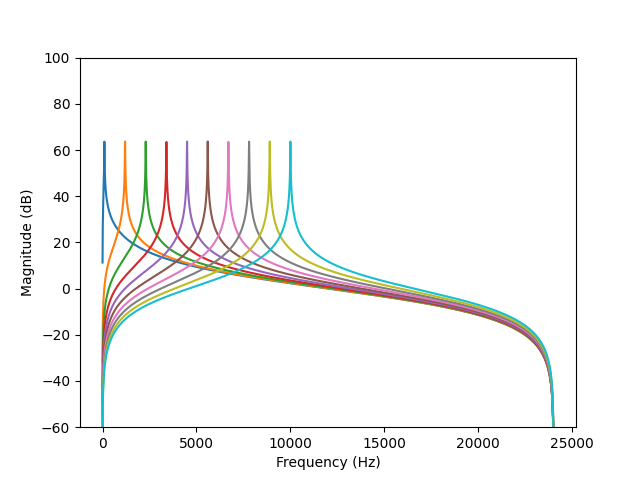
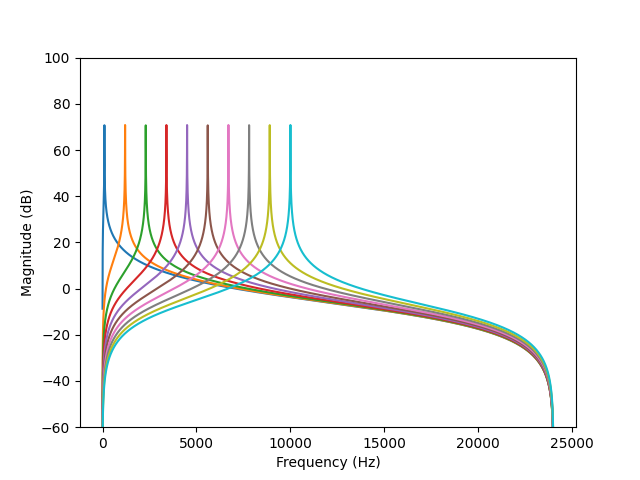
I was also trying to figure out the scaling stuff – I really wanted to have control over the output amp, not the peak gain, and it looks like the scaling factor should be sqrt(a0) rather than our a0 (for peak gain). This is both in the Stieglitz paper and csound’s version of resonz. a0 = (1 - R * R) / 2

This scaling doesn’t set amplitude to one however, they’re still too high. But it’s a good start as once it’s multiplied by sqrt(a0) rather than a0, we can just use another constant scalar rather than one that’s dependent on the parameters. The claim in the literature is that it sets the RMS to one but I don’t think I’m getting this.

sqrt(a0) experimentally results in amplitudes that are almost constant across much of the frequency range, but low frequencies with skinny bandwidths are still lower in amp – I suppose this is to be expected because there’s less time to express the frequency? I mention it because one might need to compensate for it to have low notes sound properly. And it trends very slightly upward with high frequencies. I don’t think this is because the scaling constant is wrong, just noticing details of this kind of system. Not exactly straightforward.

Anyway, my working code is now scaling the output of resonz by the (sqrt(a0) / a0) – might be good to have the sqrt(a0) factor as an option back in the ugen’s .cpp code? (as indeed csound does)

[andie]

What I meant by output amp was essentially the integral under the response curve. Stieglitz calls this the power gain (for white noise input).

I was thinking of it as summing the output amplitudes of all the frequencies, so that they sum to 1, so that (ideally) white noise at amp 1 would give you a response with amp 1.

[andie]

Nice!
I was actually just generating sound and eyeballing it in sonic visualiser as I wasn’t sure of the formula G^2
I’m much happier with your python code though!

My screenshots below: all pics have freqs ranging from 70 hz to 20000 hz; rqs are 0.1, 0.01, 0.001 for the 3 pics. I did a final multiplication by 0.1 to avoid clipping. So it looks like amplitudes are around 0.2 but they would have been around 2 – I’m not seeing where the doubling is coming from.

Here’s some code to run in scide, which shows a result around/over 2.

(
{
	var sig, ma, rez, env;
	var freq=800;
	var rq=0.010;
	var theta = (freq * 2 * 3.14159) / SampleRate.ir();
	//var theta=0.1139806858450;
	var r = 1 - ((theta * rq) / 2);
	//var r=0.9994300965710;
	var a0 = (1 - (r * r)) / 2;
	//var a0=0.0005697410342630;
	var scale = ( 1 / a0) * a0.sqrt;
	//var scale=41.89490888050;

	sig = WhiteNoise.ar();
	env = EnvGen.kr(Env([0,1,1,0],[0.001,1,0.1]));
	rez = Resonz.ar(sig * env, freq,rq) * scale;
	ma = RunningMax.ar(rez);
	[rez,ma]
}.plot(1)
)

[andie]

Aha, I get it, RMS! Thanks for the hint!

Amplitude of WhiteNoise goes almost up to 1, but its RMS is around 0.7 — so it’s uniform not Gaussian!? Yikes! SuperCollider has so many of these lovely undocumented black boxes…

The RMS output for Resonz is peaking somewhere around 1 though, so that’s good…