Why NaN from FOS here?

Questions
1

OK, I give up. Why is FOS outputting NaNs for a block here?

b = Buffer.alloc(s, 1024, 1);

(
a = {
	var sig = DC.ar(1);
	var frameCount = Sweep.ar(0, SampleRate.ir);
	var oneOverCount = frameCount.reciprocal;
	var overallAvg = FOS.ar(sig,
		a0: oneOverCount,  // new/count
		a1: 0,
		b1: (frameCount - 1) * oneOverCount
	);
	frameCount.poll(Impulse.ar(0));
	overallAvg.poll(Impulse.ar(1000));
	RecordBuf.ar(overallAvg, b, run: 1, loop: 0, doneAction: 2);
	Silent.ar(1);
}.play;
)

UGen(Sweep): 1  -- hence we are never dividing by zero
UGen(FOS): -nan  -- but...
UGen(FOS): -nan
UGen(FOS): 0.974178  -- and then a recursive filter recovers from NaN? How???
UGen(FOS): 0.298957
UGen(FOS): 0.403246

I’m guessing that FOS is incorrectly using init pre-samples at first…?

Was just trying to batch-analyze a bunch of files for overall average RMS level. SC usually doesn’t let me down… sigh

hjh

2

Answering my own question: FOS and SOS read inputs at audio rate only if ALL inputs are audio rate.

So it should be a1: DC.ar(0) :woozy_face:

(But ran out of time and I’ll have to just use sox instead… I think (?) that code snippet should converge on 1 but it converges on 1/2… for that, I really do have to give up.)

hjh

3

I think not, James. It seems there doesn’t need to be an audio rate. I think it’s just the initial coefficients and how they were initiated.

The first sample: i = 0 , and during initialization, in(i-1) and out(i-1) refer to undefined values.

It’s division by zero, indeed: oneOverCount = frameCount.max(1).reciprocal; fix it

4

I was trying to do this:

running_mean(n) = x(n)/n + running_mean(n-1) * (n-1)/n

I.e., input coefficient = 1/n, feedback coefficient = (n-1)/n, and previous feedforward coefficient = 0.

This means the coefficients must update at audio rate. This only happens when the _a calculation function is used, and _a is selected only if all inputs are explicitly audio rate. The scalar 0 causes coefficients to be read at kr. I had seen this before but forgot today. A quick glance at the source reminded me.

But, when I force audio rate, the NaN disappears.

hjh

5

I think it’s because operations (multiplication, etc) with audio signals do not output the same thing as floating-point numbers. I’m almost sure it’s a problem with initial coefficients.

The first sample is risky because there are no defined values for most of the equation.

Some situations make filters go loco: the more coefficients, the more risk:

  1. Initial state

  2. coefficients one cannot use; otherwise, the filter becomes unstable. I don’t know any filter that prevents “bad coefficients.” I found this only on Scipy, which is just for research.

  3. denormalized numbers (numbers closer to zero than e) are another danger. These numbers, which are very close to zero, also make the filters unstable. Using some functions to check is good practice, but that is not always the case.

EDIT: A simple check to handle this can be as simple as this: min_positive_value is the smallest positive normalized value represented by the floating-point type (float, double, long double). If that’s the case, change it to Zero.

We could update some filters with this function for safety, but don’t feel like defending this idea in a PR right now. It will undoubtedly have more than 50+ comments or zero :sweat_smile: -) . Of course, it does not need to be used everywhere.

template <std::floating_point T>
inline T denormal_handling (T arg) {
    const T min_positive_value = std::numeric_limits<T>::min();
    if (arg > 0) {
        if (arg < min_positive_value)
            return static_cast<T>(0.0);
        else
            return arg;
    } else {
        if (arg > -min_positive_value)
            return static_cast<T>(0.0);
        else
            return arg;
    }
}
6

Found this the other day. You could flush to zero with hardware flags and have it enabled when executing only certain code paths.

1 Like
7

Good, take note of the idea. I’m sure it has its use in some ugens.

8

There is nothing to do with audio rate!

Wouldn’t be the case to try to avoid bad coefficients in our filters? Just asking

Some helpfiles just say: “YOU MUST KNOW WHAT YOU’RE DOING”. :sweat_smile:
At the same time, there is another crew in the community that is obsessed with beginners and what is good or bad for them.

Go figures…

Ok, so that’s what happens:

  1. Initial Frame (frameCount = 0):
  2. oneOverCount = 1 / 0 = NaN
    EDIT: Corrrection: oneOverCount = (1/0) * 0 → nan
  3. b_1 = (0 - 1) * NaN = NaN
    • out(0) = NaN

For frameCount = 2:

  1. oneOverCount = 1 / 2 = 0.5
  2. b_1 = (2 - 1) * 0.5 = 0.5
  3. out(2) = (0.5 * 1) + (0 * 1) + (0.5 * 1) = 0.5 + 0.5 = 1

initial sample depends on this NaN value and it propagates (since it’s recursive). Since the initial out(i-1) is also NaN, this affects subsequent calculations, causing the output to remain NaN for some samples.

But, as it’s common, it recovers

image
image2379Ă—1979 183 KB

Disclaimer: this is a Python code with numpy library, used to calculate the behavior of digital filters

import numpy as np
import matplotlib.pyplot as plt

frameCount = np.arange(0, 50, 1)
oneOverCount = np.where(frameCount == 0, np.nan, 1 / frameCount)
b1 = (frameCount - 1) * oneOverCount

# Initialization
in_signal = np.ones_like(frameCount)
out = np.zeros_like(frameCount, dtype=float)
out[0] = np.nan

# recursive filter equation
for i in range(1, len(frameCount)):
    out[i] = (oneOverCount[i] * in_signal[i]) + (b1[i] * out[i-1])

ig, axs = plt.subplots(2, 1, figsize=(10, 8))

axs[0].plot
axs[1].plot
axs[1].grid()
plt.tight_layout()
plt.show()
9

I’d expect inf here…? 0/0 is NaN; 1/0 is inf, IIRC.

But I tested Sweep’s output and y(0) from Sweep = the increment and not 0. { var trig = Impulse.ar(0); Poll.ar(trig, Sweep.ar(0, SampleRate.ir)); FreeSelf.kr(trig <= 0); Silent.ar(1) }.play; – I’m not at the computer now but I’m pretty sure this prints 1.0.

So if FOS is getting polluted by 1/0, the only way this could happen is if the FOS constructor is receiving y(-1) as the coefficient’s initial sample.

My opinion is that it is always a mistake when a UGen returns y(-1) as its pre-sample.

Some UGens’ pre-sample is y(0); others’ is y(-1). This means that downstream units can’t assume anything about the meaning of the initial value. The only sense in which this is a good thing is that y(-1) may be easier to produce, from a code perspective. But IMO this is not a good rationale. And in fact, there’s a whole slew of weird bugs resulting from this inconsistency in the UGen library.

hjh

1 Like
10

EDIT: isn’t it (1/0) * 0 ? I think that’s what I wanted to write

But the Nan propagates in the first samples so it’s all a mess.

My personal opinion is that filters could avoid the user to ser "bad coefficients’ and "bad initialization’.

On top of that, also apply that function I posted to avoid another cause of troubles.

No, I don’t think no SuperCollider user is always safe and “knows what they’re doing”. And SC interface has not hint about it.

Unless it’s important to let the user to set bad coefficients, optionally.

EDIT: Also, to give an example, if I’m experimenting with a filter knowing the coefficients are limited to the range that the filter is stable, I will explore much more its possibilities.

Don’t you think? For example, this website implements those filters and impose those limits. I think without it, I would not play with it in the same way: Filter Playground

11

Ah… found it.

{ FOS.ar(DC.ar(1), Sweep.ar(0, 1) > 0, [0, DC.ar(0)], [0, DC.ar(0)]) }.plot;

sc-fos-bug

The top line picks up 0 from Sweep’s pre-sample and interpolates from this value to 1.

void FOS_next_k(FOS* unit, int inNumSamples) {
    float* out = ZOUT(0);
    float* in = ZIN(0);
    float next_a0 = ZIN0(1);
    float next_a1 = ZIN0(2);
    float next_b1 = ZIN0(3);

    double y1 = unit->m_y1;
    double a0 = unit->m_a0;
    double a1 = unit->m_a1;
    double b1 = unit->m_b1;
    double a0_slope = CALCSLOPE(next_a0, a0);
    double a1_slope = CALCSLOPE(next_a1, a1);
    double b1_slope = CALCSLOPE(next_b1, b1);

    ...
}

But the bottom line shows that Sweep’s true output is always nonzero: Sweep.ar(0, 1) > 0 is always 1 for sample index >= 0. This means the top line is picking up y(-1).

I haven’t yet heard a rationale why pre-sample = y(-1) is good, except for “it’s too hard to change” (which is just a cop-out).

hjh

1 Like
12

FOS help:

Formula is equivalent to:

out(i) = (a0 * in(i)) + (a1 * in(i-1)) + (b1 * out(i-1))

FOS source:

    double y0 = in + b1 * y1;
    ZOUT0(0) = a0 * y0 + a1 * y1;
    y1 = y0;

These certainly don’t behave the same.

(
r = Routine { |inval|
	var avg = 0.0, n = 0, recip;
	var avg2 = 0.0, a0, a1 = 0, b1, y0, y1 = 0;
	loop {
		n = n + 1;
		a0 = n.reciprocal;
		b1 = 1 - a0;

		avg = (a0 * inval) + (b1 * avg);
		y0 = inval + (b1 * y1);
		avg2 = a0 * y0 + (a1 * y1);
		inval = [avg, avg2].yield;
		y1 = y0;
	}
};
)

10.do { r.next(1).postln };

[1.0, 1.0]
[1.0, 0.75]
[1.0, 0.66666666666667]
[1.0, 0.625]
[1.0, 0.6]
[1.0, 0.58333333333333]
[1.0, 0.57142857142857]
[1.0, 0.5625]
[1.0, 0.55555555555556]
[1.0, 0.55]

So “equivalent to” is flat wrong in the docs.

hjh

1 Like
14

James, I think some design would have to be changed to avoid those things. The SynthDef would have to be checked before initialization, because the calculation is… not quite that simple.

Do you know how that could be done with current model?

Just for illustration, this is a code in Haskell that calculates that. It involves complex numbers and some computations that may not be cheap.

EDIT: Would be nice to benchmark the cost of checking this in an optimized real-time code. Actually, it doesn’t need to check at audio rate, but much lower rates or demand rates

import Data.Complex (Complex((:+)))

data IIRParams = IIRParams
    { b0 :: Float
    , b1 :: Float
    , b2 :: Float
    , a0 :: Float
    , a1 :: Float
    , a2 :: Float
    }
    deriving (Show)

-- Example of an unstable filter (IIR BAD Coefficients)
unstableFilter :: IIRParams
unstableFilter = IIRParams
    { b0 = 0.5
    , b1 = 0.5
    , b2 = 0.5
    , a0 = 1.0
    , a1 = -1.8  -- These coefficients
    , a2 = 0.9   -- produce poles outside 'circle'
    }

-- Calculate poles of IIR filters
calculatePoles :: IIRParams -> (Complex Float, Complex Float)
calculatePoles (IIRParams _ _ _ a0 a1 a2) =
    let discriminant = a1 * a1 - 4 * a0 * a2
        twoA = 2 * a0
        sqrtDisc = sqrt discriminant
        realPart = (-a1) / twoA
        imagPart = sqrtDisc / twoA
        root1 = realPart :+ imagPart
        root2 = realPart :+ (-imagPart)
    in (root1, root2)


-- Magnitude of complex numbers
magnitude :: Complex Float -> Float
magnitude (r :+ i) = sqrt (r * r + i * i)

-- Check IIR filter is stable
isStable :: IIRParams -> Bool
isStable params =
    let (pole1, pole2) = calculatePoles params
    in magnitude pole1 < 1 && magnitude pole2 < 1

main :: IO ()
main = do
    let params = unstableFilter
    print params
    print $ calculatePoles params
    print $ isStable params  -- should be False

The theory comes from here: Audio EQ Cookbook

One needs to calculate two things:

  1. The calculatePoles finds the roots of the characteristic equation; the equation that represents the poles of the filter. The characteristic equation is the filter transfer function denominators setting them equal to zero, then multiplying this by z^2

$a_0 + a_1 z^{ -1} + a_2 z^{-2} = 0$ then multiply this by z^2 → $ a_0 z^2 + a_1 z + a_2 = 0 $
image ----> image

  1. The isStable function ensures both poles have magnitudes less than 1.
16

I appreciate the thorough approach above, but perhaps that’s for a different thread?

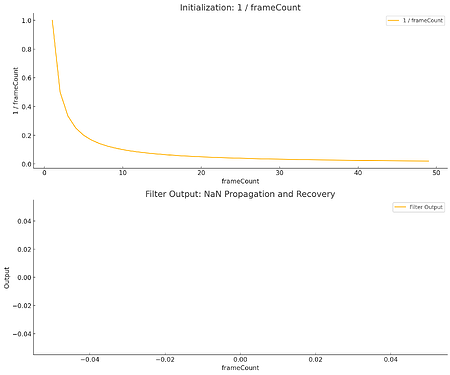
This thread is about a very specific case. The idea is to produce a running average – not a moving average (where SC already has the incorrectly-named RunningSum, which you can divide by the window size to get a moving average) – a true running average, which keeps accumulating indefinitely.

I was using FOS to try to achieve this, because a moving average can be implemented as a first-order recursive filter:

moving_avg(x(n)) = (1/n) * x(n) + (1 - 1/n) * y(n-1)

I.e., a0 = 1/n, b1 = 1 - (1/n).

The answer to the title question has two parts:

First, 1/0 and 0.reciprocal return different results in the server (while returning the same result in the language):

[0.reciprocal, 1/0];
-> [inf, inf]

s.boot;

(
f = { |sig|
	{
		var trig = Impulse.ar(0);
		Poll.ar(trig, sig.value);
		Silent.ar(1)
	}.play;
};

f.({ var x = DC.ar(0); [x.reciprocal, 1/x] });
)

UGen(UnaryOpUGen): -nan
UGen(BinaryOpUGen): inf

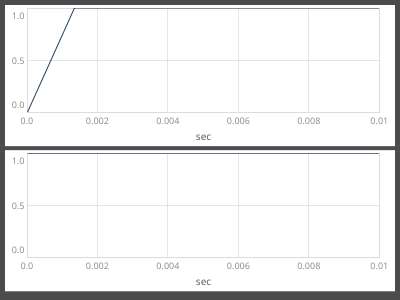
Second, that 0.reciprocal should never be entering FOS at all. The first sample, y(0), of Sweep.ar(trig, SampleRate.ir) is 1.0. Thus it can be entering FOS only in the Ctor. My opinion is that it’s a remaining bit of sloppiness in the SC plugin interfaces, that the Ctor “pre-sample” currently is either y(0) or y(-1), at the whim of each plug-in, which of course has no idea which value is expected downstream. The only way that you can have a consistent expectation downstream is if that initial value being produced is consistent.

The NaN’s here are not FOS’s fault. They’re Sweep’s fault.

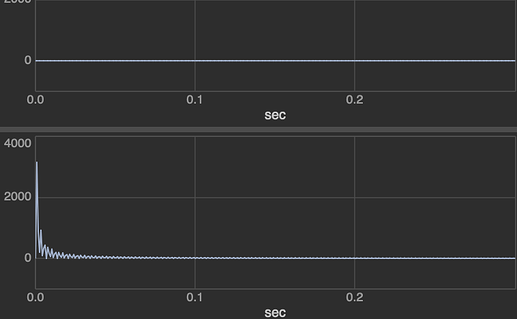
THEN… having resolved that by forcing audio rate coefficients, which causes the 0.reciprocal to be discarded before it affects FOS results, I found that FOS’s behavior does not match the documented “equivalent” formula.

I guess the UGen is trying to do a DR-II or TDR-II formula, to save one delay register, but the formula must be written incorrectly.

    double y0 = in + b1 * y1;
    ZOUT0(0) = a0 * y0 + a1 * y1;
    y1 = y0;

a0 * y0 + (a1 * y1) expands to (a0 * in) + (a0 * b1 * y1) + (a1 * y1) which reduces to (a0 * in) + ((a0 * b1 + a1) * y1) – now here, I’ll admit that my math isn’t good enough – but in the specific running-average case, first a0 = 1, first b1 = 0. So, first cycle, y0 = in(0), output = y0 * 1 + 0 * 0 = in(0), and second cycle starts with y1 = in(0). Then new a0 = 0.5, new b1 = 0.5, new y0 = in(1) + 0.5 * in(0), new out = 0.5 * (in + 0.5 * in(0)) so the feedback coefficient here is really 0.25, NOT 0.5 as supplied.

This can’t be right.

So I’d like to suggest that the purpose of this thread be to identify what is wrong with the formula that is causing this non-equivalent behavior. General filter safety is a different problem.

hjh

17

Some brainstorming ideas… (sketchy) just workarounds? rs

// In FOS_Ctor
unit->m_a0 = ZIN0(1) == 0 ? 1 : ZIN0(1); // a0 is NEVER zero



if (std::isnan(next_a0) || std::isnan(next_a1) || std::isnan(next_b1) || std::isinf(next_a0) || std::isinf(next_a1) || std::isinf(next_b1)) {
    next_a0 = 1; next_a1 = 0; next_b1 = 0;
}

EDIT
The irony of the SC3 ugen source structure is that it has a special place for initialization, and then it does not do the job to initialize the filters properly )))

18

How does this fix the wrong calculation?

hjh

19

Nothing, just aiming at safe initialization. ex:

unit->m_a0 = ZIN0(1);
unit->m_a1 = ZIN0(2);
unit->m_b1 = ZIN0(3);

// to

unit->m_a0 = std::isnan(ZIN0(1)) || std::isinf(ZIN0(1)) ? 1 : ZIN0(1);
unit->m_a1 = std::isnan(ZIN0(2)) || std::isinf(ZIN0(2)) ? 0 : ZIN0(2);
unit->m_b1 = std::isnan(ZIN0(3)) || std::isinf(ZIN0(3)) ? 0 : ZIN0(3);

The calculation is an equation. If it’s not what the helpfile says… I don’t know what to do. “Correct it”?

20

To create a running average that accumulates indefinitely , you need to keep track of the running sum of the signal and divide it by the number of samples processed so far.

Is that what you said? (maybe I just don’t know the concept)

{   var sig, runningAvg, trig, sr, count;
    sig = SinOsc.ar(440, 0, 0.1);  
    sr = SampleRate.ir;
    count = Sweep.ar(Impulse.ar(0), 1);  
        runningAvg = Integrator.ar(sig) / count;
   [sig, runningAvg]
}.plot(0.3)

image
image758Ă—468 13.2 KB

21

Yes, that’s what a running average is.

(Sigma [i = 1 … n] x(i)) / n

But this is equivalent to the recursive formula. Consider the case of n = 2, average = (a + b) / 2. Then the average for 3 samples = ((a+b)/2) * 2/3 + (c/3) = (a+b)/3 + (c/3) = (a+b+c)/3 and inductively it can be seen that this will extend indefinitely up to any n.

The potential advantage is that after a large number of values, the integrator may reach such a high magnitude that floating point addition may no longer produce a correct result – but the feedback term will remain in the same range (though dividing the new value by n might not be much better, I guess).

FOS’s documentation says you can render this formula using the coefficients that I tried (and my Routine test confirms this). But the behavior is discrepant. I think we should fix the discrepancy, but first I’d like to understand how the formula in FOS’s C++ source is related to the “equivalent” formula in the docs. Or perhaps this is a question for dsp stackexchange…?

hjh

22

Those edge cases make me think it would be useful to instantiate Graphs with another Float type, such as double, or long double (pushing the limit of the compiler), or even higher sampling rates in other cases. Not just a curiosity.

It might be useful to do a Faust version and compile with other flags and types