So let’s start with the easiest way to do this. In extras there’s a SyncSaw ugen that handles synching for us. Unfortunately it’s not anti-aliased, so let’s get a sense of what that means. First of all let’s fire up a frequency scope:
FreqScope.new();
Then play the synth below and switch between buses 0 and 1 on the frequency scope:
{[LFSaw.ar(1000), Saw.ar(1000)]}.play
So with the aliasing version on bus 0, and the anti-aliased version on bus 1 you should be able to see (and maybe hear) the difference. The aliasing is pretty bad. We can improve things a little:
{[LFSaw.ar(1000), HPF.ar(LFSaw.ar(1000), 900), Saw.ar(1000)]}.play
Bus 1 is better, but we still have a lot of noise between the fundamentals. So this is far from perfect. Let’s not worry about that for the moment. Evaluate the following function:
(
/* fFreq = Fundamental Frequency
sFreq = Saw Frequency
*/
f = {|fFreq, sFreq, cycles=5|
var x = {[
SyncSaw.ar(fFreq, sFreq),
LFSaw.ar(fFreq).range(-0.5, 0.5),
]};
x.plot(cycles/fFreq);
}
)
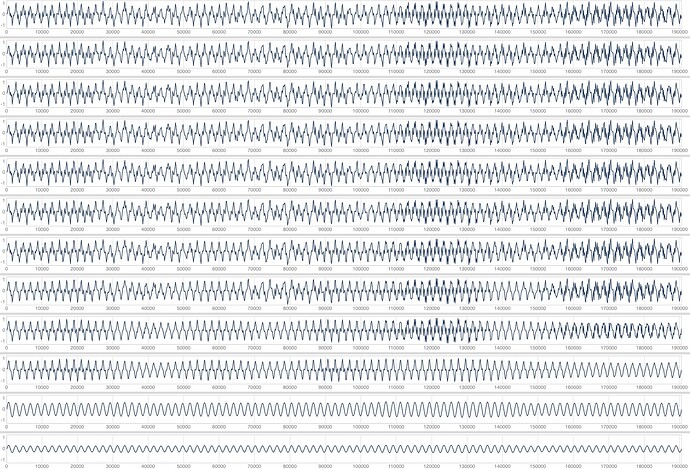
This function will plot the output of the syncsaw on the top graph, with a reference saw wave below. This will give you a sense of t
fFreq is the frequency of the sync wave and sFreq is the frequency of our output saw wave. So our saw wave is being reset fFreq times per second, but the saw wave’s frequency is sFreq. Too much theory, let’s draw stuff:
f.(100, 100);
So this just a saw wave. Our sync oscillator is resetting our saw wave when our saw wave reaches a phase of 0. Let’s try some more values:
f.(100, 200);
If you ignore the second wave which is some kind of weird artefact, you can see that we have doubled the frequency.
f.(100, 300);
and so on. Let’s do something more interesting:
f.(100, 150);
(again ignore the second wave). So this time our periodic frequency is unchange, but our wave is split into two waves. The first saw wave which has the frequency of our saw wave, the second wave which has a smaller frequency with a range of -1 to 0.
f.(100, 250);
and let’s look at the frequency components:
{SyncSaw.ar(100, 200)}.play
So our fundamental here has been shifted (as we’d expect) from the saw wave (remember to do cmd-period/ctrl-period each time):
{Saw.ar(100)}.play
Playing around a bit more:
f.(100, 120)
{SyncSaw.ar(100, 200)}.play
So essentially when we double the saw frequency, we double the fundamental of the overall wave, which makes sense.
Whereas the faction changes the timbre, with fractions closer to the next number shifting the energy into the next harmonic:
f.(100, 120)
{SyncSaw.ar(100, 120)}.play
f.(100, 280)
{SyncSaw.ar(100, 280)}.play
So whole number ratios shift us up an octave, fractional values change the timbre (though inevitably higher fractions will also shift the perceived tone). I suspect, though I haven’t checked, that the more imperfect the ratio between the fundamental and audio wave frequencies, the wilder the timbre. Feel free to check.
How about we cross the streams:
f.(300, 227.3)
So there’s nothing stopping us doing this, it’s just fairly uninteresting. We’re just reducing the amplitude and DC biasing our signal. So when doing hard sync always make the /fundamental/ lower than the audio wave. And when working out the affect remember:
- fundamental defines the fundamental note.
- The ratio of the audio wave frequency to the audio wave frequency defines the note we hear and the timbre.
So if we have a fundamental of 100hz and a saw wave of 243hz. the output wave will have a frequency of 200 hz, and and the 43 hz will affect our timbre.
That’s part one. Feel free to tell me what’s wrong and I’ll correct it. Part two will come whenever I find time and will start looking at some audio applications and ways to implement it in supercollider.
If you’re oversampling I think you could probably get away with octaves.
