Frequency instead of phase

Questions
1

hey, how can i get the exact same behaviour from the curved downward sweep when instead using frequency fm instead of driving the phase pm. With the Osc i want to use Squine you can unfortunately only define the initial phase. thanks

(
{
	var freq = 100;
	var formantFreq = 400;
	var trig = Impulse.ar(freq);

	var phase = Sweep.ar(trig, formantFreq);

	var pm = SinOsc.ar(0, (1 - phase) ** 3 * 2pi);
	var fm = SinOsc.ar(formantFreq * (1 + (phase)), pi);

	pm = pm * (phase < 1.0);
	fm = fm * (phase < 0.99);

	[pm, fm];

}.plot(0.02);
)
1 Like
2

A starting point is to observe that frequency is the derivative of phase. Some basic calculus tutorials online should explain what “derivative” is… but consider. When you produce phase by, for instance, Phasor.ar(0, freq * SampleDur.ir, 0, 1), freq * SampleDur.ir is an increment that is added to the phase every time. So to go from frequency to phase, the operation is integration. A constant frequency integrates to a ramp – picture it in your head; intuitively this makes sense.

The inverse operation of integration is differentiation – slope of the curve. So to get the same effect as a phase formula, but using a frequency input, you differentiate the phase – calculus word is “derivative.”

Mathematicians worked out a lot of formulas already, which you can find online. I haven’t touched calculus since high school, but a quick search finds that the derivative of x ^ 3 is 3x^2 dx where for our purposes we can disregard the delta notation dx.

2pi · (1 - p) ^ 3

// derivative:
2pi · 3 · (1 - p)^2
6pi · (1 - 2p + p^2)

So if I’ve done the algebraic manipulations right, 6pi * (phase.squared - (2 * phase) + 1) as a frequency is a starting point.

Unfortunately I can’t test right now, so there may be another times or divide factor, possibly related to sample rate. Also if Squine reads phase as 0 to 1 instead of 0 to 2pi, then 6pi in that formula would have to become 3 instead.

hjh

1 Like
3

thanks alot for the explanation. i will have a deeper look into those formulas.

ive tried out:

as frequency

(
{
    var snd, snd2, freq, trig, formantFreq, phase;

    freq = 100;
	formantFreq = 400;

	trig = Impulse.ar(freq);
	phase = Sweep.ar(trig, formantFreq);

	snd = SinOsc.ar(0, (1 - phase) ** 3 * 2pi);
	snd = snd * (phase < 1);

	snd2 = SinOsc.ar(6pi * (phase.squared - (2 * phase) + 1));
	snd2 = snd2 * (phase < 0.99);
	
	[snd, snd2];

}.plot(0.02);
)

but unfortunately i doesnt get there and its also not constant for every duty cyle.

4

I’m afraid I don’t have access to my machine for the next day or two so there is nothing more that I can do at the moment.

One other question is: how do they sound? For example, comparing FM vs PM, they sound practically identical for modulators with no DC component, but you will see a phase shift in the graphs (because the derivative of a sinusoidal phase modulator is also sinusoidal, but with a 90 degree phase difference). So you might not need 100% perfectly identical graphs.

What I mean is: your phase formula starts at a nonzero value, but this initial value gets lost when differentiating. This would account for a different visual appearance of the waveform, but the visual difference may be inaudible. If people will be listening to your signal rather than looking at it, then the plot may not be important.

EDIT: While the above is valid, I just realized that it doesn’t account for the discontinuity in the phase input when phase resets to 0. This would also have to be differentiated and added into the frequency formula. I don’t have that ready right now, though – I’m finding myself unable to improvise the solution in the forum editor, needs more time.

hjh

5

Going back to the original question – “exact same behaviour from the curved downward sweep when instead using frequency fm instead of driving the phase pm” – I have to admit that my math skills are not up to the task. So my best suggestion, I guess, is find an applied mathematician, take them out for a beer, and see if they know.

Having pondered it, and played with some formulas on paper, I still haven’t quite got it right. I got as far as a formula for a changing frequency that should cause phase to follow the curve (1 - linphase) ^ 3. But the units are important. This “linphase” is measured as… 1.0 = one complete wave cycle? Radians? That (1 - x) ^ 3 is measured 1.0 = wave cycle at least but I’m quite muddled about the relationship to the Sweep value.

One problem in your SynthDef: With the given settings, I believe the Sweep will output 0 to 4.0, meaning the phase would be 2pi to -27×2pi. SinOsc is not stable when phase exceeds ±8pi, you’re at -54pi, so you’re already in trouble. You can fix it by taking the phase curve % 1.0 * 2pi – but that then makes it trickier to calculate a momentary reset frequency.

I can safely say that you cannot accidentally stumble onto a formula that will give you the exact same behavior. The only way there is by some good old fashioned algebra, based on defining the problem systematically (which hasn’t been done yet). So my suggestion above is really, if you don’t have good enough algebra (I’m admitting that I don’t – I might be able to handle a chunk of it if the problem is well defined, but I find myself unsituated to fix the problem definition), then, find someone who does. Alternately, you could choose to accept inexact results.

hjh

6 
(
{
    var snd, snd2, freq, trig, formantFreq, t, phase, dphase;

    freq = 100;
	formantFreq = 400;

	trig = Impulse.ar(freq);
	t = Sweep.ar(trig, formantFreq);
	phase = 2pi * ((1-t) * (1-t) * (1-t));
	dphase = 6pi.neg * (1-t).squared;
	dphase = dphase / (pi/2 + 0.065) ; // nudge

	snd = SinOsc.ar(0, phase.mod(2pi));
	snd = snd * (phase < 1);

	snd2 = SinOsc.ar(dphase * freq);
	snd2 = snd2 * (phase < 1);
	
	[snd, snd2]
}.plot(0.02);
)

The plot looks pretty close, but it sounds quite different.

7

thanks for all the replies :slight_smile:

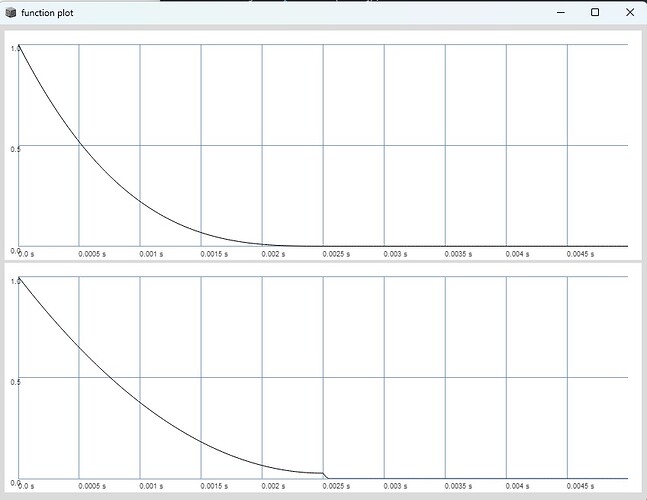
defining freq and formantFreq like in the example above follows the pulsar synthesis chapter in microsound where the pulsaret length (grain duration) is always equal to 1 / formantFreq followed by silence until the next trigger arrives for the case formantFreq > freq. Both of the parameters can be modulated independently. The rectangular window in this case applied with phase < 1 should always have the length of the pulsaret. the pulsaret is always only one cycle of the waveform unless its beeing multiplied by an integer: sin((1 - phase ) ** 3 * 2pi * sineCycles.kr(4)) which concatenates a number of single cycles under the window function.
Therefore the window function in the example by @bovil43810 should be adjusted to t < 1 instead of phase < 1

(
{
    var snd, snd2, freq, trig, formantFreq, t, phase, dphase;

    freq = 100;
	formantFreq = 400;

	trig = Impulse.ar(freq);
	t = Sweep.ar(trig, formantFreq);
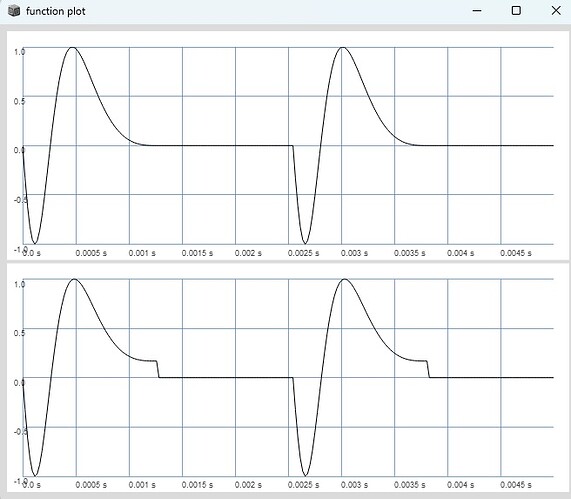
	phase = 2pi * ((1-t) * (1-t) * (1-t));
	dphase = 6pi.neg * (1-t).squared;
	dphase = dphase / (pi/2 + 0.065) ; // nudge

	snd = SinOsc.ar(0, phase.mod(2pi));
	snd = snd * (t < 1);

	snd2 = SinOsc.ar(dphase * freq);
	snd2 = snd2 * (t < 1);
	
	[snd, snd2]
}.plot(0.02);
)

EDIT: im not sure if dphase should be multiplied by freq. i think it should be multiplied by formantFreq.
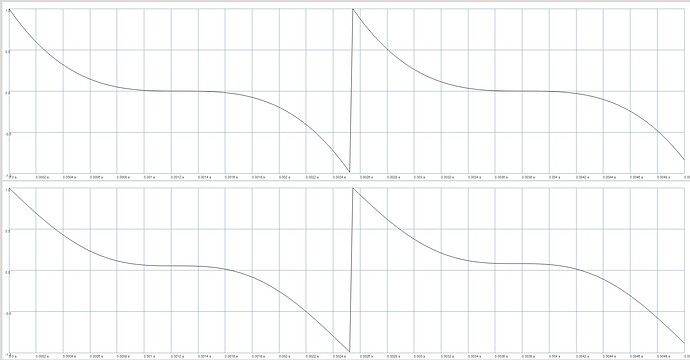
when you get rid of the curving thats aquivalent:

(
{
    var snd, snd2, freq, trig, formantFreq, phase, sineCycles;

    freq = 100;
	formantFreq = 400;
	sineCycles = 2;

	trig = Impulse.ar(freq);
	phase = Sweep.ar(trig, formantFreq);

	snd = SinOsc.ar(0, phase * 2pi * sineCycles);
	snd = snd * (phase < 1);

	snd2 = SinOsc.ar(formantFreq * sineCycles);
	snd2 = snd2 * (phase < 0.99);
	
	[snd, snd2]
}.plot(0.02);
)

thanks a lot for making the effort to adjust it for beeing used as frequency instead of phase. My algebra / DSP is unfortunately not sufficient enough to know why both of these create different results.

I havent taken SinOscs limitation of ±8p into account thanks for pointing that out @jamshark70
i now see the reason why probably using sin((1 - phase ) ** 3 * 2pi) makes more sense here, or?
Also thanks for pointing out the necessity for the phase reset.

after looking at how “total phase” is defined and the comparision of FM and PM in this thread Frequency Modulation – Phase Modulation – Delay Modulation (FM / PM / DM)
i thought freq and phase would easily be interchangeable. Seems to be more complicated then i thought, sorry for the noise.

As always, some concepts i try to merge (in this case the chirp beeing used for Pulsar Synthesis + the possibility for aliasing free high index FM on Sin/Saw/Square which needs Squine) are simply not possible or easily not possible.

My specific pulsar implementation was taken from / inspired by @nathan wonderful blog post Pulsar Synthesis | Nathan Ho

8

thats the first derivation, so far so good:

dphase = 6pi.neg * (1-t).squared;

but whats the nudge? @bovil43810

dphase = dphase / (pi/2 + 0.065); // nudge
9

That was just me noticing the waveform drifting over time, which I thought could be fixed by multiplying the phase by some symbolic constant. The 0.065 was just based on messing around trying to find such a constant, which didn’t really work obviously. It probably sounds like a stupid way to go about figuring out things like this (which it is, I know) but I’ve been able to solve some problems using this brute force approach, sometimes using RIES or other inverse symbolic lookup tools. Apologies for just kind of dumping that code on you without any further explanation.

10

What’s the reasoning behind using that exact function ((1-phase)**3 * 2pi) instead of just generating a pitch envelope using Env to get a sine chirp? How did you arrive at it? It’s not in the pulsar chapter in Microsound. If you can’t get an exact number of cycles within the formant period by finding an analytic solution (moving from PM to FM), you can just use a “softer” window than rectangular (e.g. expodec) and won’t get any discontinuities.

11

It’s not clear to me exactly what kind of result you’re looking for here, especially where FM comes into play. Are you simply trying to do pulsar synthesis with sine chirp pulsarets? Chirps (or chirplets, in this case) obviously already require frequency modulation (a downward or upward pitch sweep). What I’m getting at is: I don’t think what you’re trying to achieve is necessarily impossible because the PM to FM conversion you originally asked about is difficult to figure out analytically, because there may very well be other ways of achieving the same thing that don’t require that sort of derivation, but it’s hard to help you if we don’t know what you’re actually trying to do. Maybe @nathan can help us out here, since they mentioned using downward sine chirps as pulsarets in their blog post, but didn’t include any code examples for that pulsaret type.

12

thanks for explaining the nudge.
i think for that reason you need to take in account the phase reset.

the formula ((1-phase)**3 * 2pi) comes from @nathan i didnt wanted to bother him any more with all my questions and made it public in the forum. its discribed in his “moisture bass” blog post: Moisture Bass | Nathan Ho
I also thought that the question is more a general one about FM and PM and not so specific about the curved downward sweep. so maybe others would also be interested in the discussion.

the frequency modulation doesnt necessarily come into play there.
i just want to be flexibile enough when writing SynthDefs.
I dont always want to use the chirp and i dont always want to use FM when using patterns to control the instrument.
But both of these things need a different setup at the moment which makes it not possible to interpolate between different timbres.
At the moment i have about 10 SynthDefs which all do some kind of pulsar synthesis. They are similar but not identical. With all of them i was able to create “sound objects” i like. To then compose “timbral evolutions” of these sound objects the different timbres need to be able within the same SynthDef. Thats just my way of doing things in relation to composition.
So i would like to merge some of those concepts which is harder then it seemed to have just one or two SynthDefs in the end.

ive already tried out to use a freq envelope function with a downward sweep scaled to the pulsaret duration or buffered signals for FM driven by the phase. thats cool but you dont get there.

in terms of the envelope generator as far as i understand it:
i think EnvGen would not work here when you modulate freq and formantFreq. you need a stateless envelope function which is driven by the phase.
Therefore i have been trying out IEnvGen. whichs works but is not modulateble which makes it very unflexible.
Ive also tried out buffers which have different problems when switching them and using audio triggers. (BufRd only changes at control rate).

EDIT:
im sorry if have been unprecise. i think one thing about asking questions is that you dont know all the details which are necessary to solve the task. so my initial post was my attempt to formulate the question in the most condensed way i was able to. thanks for taking some time :slight_smile:

13

I haven’t taken the time to read through and fully understand this thread, so sorry if I’m missing something basic, but I can explain my chirp formula.

I start with a periodic signal, called pulsaretPhase in my blog post, that is 0 at the beginning of the pulsaret, 1 at the end, and continues linearly increasing during the silence at the same rate before resetting to 0 at the start of the next pulsaret. It looks like a saw wave signal, so I used an LFSaw to generate it. You can also use Sweep/Impulse if you want.

To get a single sine wave cycle for your pulsaret, the formula is (pulsaretPhase * 2pi).sin. To get multiple sine wave cycles, use (pulsaretPhase * numSineCycles * 2pi).sin.

Now, to get a chirp, I use a nonlinear function of pulsaretPhase as an input to the sin function. The nonlinear function I decided to use was x ** 3, which curves the range [0, 1] so that it starts off slow, speeds up and rapidly approaches 1. However, a chirp starts off fast and slows down, so we use the time reversal of this instead: (1 - x) ** 3. The resulting pulsaret function is therefore ((1 - pulsaretPhase) ** 3 * numSineCycles * 2pi).sin. This is what I used in the second audio example in my blog post.

I haven’t tried combining FM or PM with pulsar synthesis, so I don’t know anything about that.

1 Like
14

I tried to write down the derivation @dietcv asked for in the original post to see whether I made any mistakes. Bascially, it boils down to finding the instantaneous frequency given the instantaneous phase, like hjh said.

We start by writing out the phase modulation formulation:

y(t) = sin((1 - phase) ** 3 * 2pi), where phase = t * formantFreq
y(t) = sin((1 - (t * formantFreq)) ** 3 * 2pi)

We denote the argument of the sine, which is the instantaneous phase, as phi(t):

y(t) = sin(phi(t)) where phi(t) = (1 - (t * formantFreq)) ** 3 * 2pi)

Then, the instaneous frequency, which is the derivative of the phase and denoted omega(t) = phi'(t) = d/dt phi(t), can be calculated as follows:

phi'(t)  = d/dt (1 - (t * formantFreq)) ** 3 * 2pi)
phi'(t) = 2pi * d/dt (1 - (t * formantFreq)) ** 3)                              // take out constant
phi'(t) = 2pi * 3 * ((1 - (t * formantFreq)) ** 2) d/dt (1 - (t * formantFreq)) // apply chain rule: d/dt (t**a) = a * ( t**(a-1))
phi'(t) = 2pi * 3 * ((1 - (t * formantFreq)) ** 2) * (-formantFreq)             // d/dt (1 - (a*t)) = -a

which simplifies to:

omega(t) = phi'(t) = -6pi * formantFreq * ((1 - (t * formantFreq)) ** 2)

However, that gives us the instantaneous angular frequency (in rad/s), which we still need to convert to the instantaneous ordinary frequency (in Hz):

f(t) = omega(t) / 2pi = -3 * formantFreq * ((1 - (t * formantFreq)) ** 2)

Translated to code:

(
{
	var t, phi, f, fm, pm;
	var freq = 100;
	var formantFreq = 400;	
	
	t = Sweep.ar;
	phi = (1 - (t * formantFreq)) ** 3 * 2pi;
	f = 3.neg * formantFreq * (1 - (t * formantFreq)).squared;

	pm = SinOsc.ar(0, phi.mod(2pi));
	fm = SinOsc.ar(f);

	[pm, fm]
}.plot(0.01).superpose_(true).plotColor_([Color.red, Color.green]);
)

Unfortunately, there still is a visible and audible discrepancy in the result which I can’t explain, but the conversion method itself is sound.

15

thanks alot for the detailed explanation :slight_smile:

When you add the rectangular window like in my initial example, you can see that the phase reset is still a problem, every pulsaret is different.
When you additionally change freq and FormantFreq you see that the difference between the two formulas is even bigger.

(
{
	var t, phi, f, fm, pm;
	var freq = 100;
	var formantFreq = 800;
	var trig = Impulse.ar(freq);

	t = Sweep.ar(trig);
	phi = (1 - (t * formantFreq)) ** 3 * 2pi;
	f = 3.neg * formantFreq * (1 - (t * formantFreq)).squared;

	pm = SinOsc.ar(0, phi.mod(2pi));
	fm = SinOsc.ar(f);

	pm = pm * (t * formantFreq < 1.00);
	fm = fm * (t * formantFreq < 1.00);

	[pm, fm]
}.plot(0.02).superpose_(true).plotColor_([Color.red, Color.green]);
)
16

ive experimented a bit more with fm and pm for pulsar synthesis. still trying to find out how to make these two expressions identical, to be able to get rid of the curved phase and have a more versatile fm expression.
what kind of FM modulator do you need for having an ordinary fm approach like this:

fm_phase = Sweep.ar(trig, grainFreq * (1 + (fmod * index)));

and be able to get the same result? thanks

(
{
	var tFreq = 100;
	var grainFreq = 400;
	var trig = Impulse.ar(tFreq);
	
	var pm_phase = Sweep.ar(trig, grainFreq);
	var fm_phase = Sweep.ar(trig, grainFreq * (1 + (LFSaw.ar(grainFreq, 1) * \index.kr(1))));

	var pm = sin((1 - pm_phase) ** 3 * 2pi);
	var fm = sin(fm_phase * 2pi);

	pm = pm * (pm_phase < 1.00);
	fm = fm * (fm_phase < 1.00);

	[pm, fm]
}.plot(0.02);
)

when i look at the phases there is this little bump in the end for FM, whats causing this? Its not so much about the plot, but they are also sounding differently and i would like to get rid of (1 - fm_phase) and have fm_phase instead.

(
{
	var tFreq = 100;
	var grainFreq = 400;
	var trig = Impulse.ar(tFreq);

	var pm_phase = Sweep.ar(trig, grainFreq);
	var fm_phase = Sweep.ar(trig, grainFreq * (1 + LFSaw.ar(grainFreq, 1).neg));
	
	var pm_grainWindow = pm_phase < 1;
	var fm_grainWindow = fm_phase < 1;
	
	pm_phase = (1 - pm_phase) ** 3;
	fm_phase = (1 - fm_phase);
	
	pm_phase = pm_phase * pm_grainWindow;
	fm_phase = fm_phase * fm_grainWindow;
	
	[pm_phase, fm_phase];
}.plot(0.005);
)

asdasdasd
asdasdasd848Ă—655 49.1 KB

17

if its necessary i could also think of using PlayBuf as a modulator for FM with a buffered single cycle signal to get the desired result.

18

made some further adjustments, still not sure how to get the curved phase with the FM approach.

(
{
	var tFreq = 400;
	var grainFreq = 800;
	var trig = Impulse.ar(tFreq);
	var overlap = 2;

	var pm_phase = Sweep.ar(trig, grainFreq);

	//var fmod = (grainFreq / tFreq) - Sweep.ar(trig, grainFreq);
	//var fm_phase = Sweep.ar(trig, grainFreq * fmod);

	var fm_phase = Sweep.ar(trig, grainFreq * (1 + SinOsc.ar(tFreq, 0.5pi)));

	var pm_grainWindow = pm_phase / overlap < 1;
	var fm_grainWindow = fm_phase / overlap < 1;

	pm_phase = (1 - pm_phase) ** 3;
	fm_phase = (1 - fm_phase);

	pm_phase = pm_phase * pm_grainWindow;
	fm_phase = fm_phase * fm_grainWindow;

	[pm_phase, fm_phase];
}.plot(0.005);
)

asdada
asdada1909Ă—997 165 KB

19

Just throwing this into the conversation, Bill Schottstaedt offers a very nice overview in his An Introduction To FM. In his introduction, Schottstaedt states “… there is no essential difference between frequency and phase modulation.”

Schottstaedt presents a number of implementations (in CLM), along with analysis and discussion.

1 Like
20

thanks for the link. this is a real headscratcher to me:

(
{	
	var tFreq = 400;
	var trig = Impulse.ar(tFreq);
	var grainFreq = 800;
	var overlap = 1;
	
	var phase = Sweep.ar(trig, grainFreq);
	
	var fmod = 3.neg * (1 - Sweep.ar(trig, grainFreq)).squared;
	var fm_phase = Sweep.ar(trig, grainFreq * fmod);
	
	var grainWindow = phase / overlap < 1;
	
	var pm_sig = sin((1 - phase) ** 3 * 2pi);
	var fm_sig = sin(fm_phase * 2pi);
	
	pm_sig = pm_sig * grainWindow;
	fm_sig = fm_sig * grainWindow;

	[pm_sig, fm_sig];
}.plot(0.005);
)

asdagaga
asdagaga656Ă—574 53.3 KB 

(
{
	var tFreq = 100;
	var trig = Impulse.ar(tFreq);
	var grainFreq = 400;
	var overlap = MouseY.kr(1, 2);

	var phase = Sweep.ar(trig, grainFreq);

	var fmod = 3.neg * (1 - (Sweep.ar(trig, grainFreq))).squared;
	var fm_phase = Sweep.ar(trig, grainFreq * fmod);

	var pm_grainWindow = phase / overlap < 1;
	var fm_grainWindow = fm_phase / overlap < 1;

	var pm_sig = sin((1 - phase) ** 3 * 2pi);
	var fm_sig = sin(fm_phase * 2pi);

	var sig;
	
	pm_sig = pm_sig * pm_grainWindow;
	fm_sig = fm_sig * pm_grainWindow;

	sig = LinXFade2.ar(pm_sig, fm_sig, MouseX.kr(-1, 1));
	sig !2 * 0.1;
	
}.scope;
)