Frequency instead of phase

[dietcv]

thanks for your further explanations.

i think one solution then would be to stay with PM but exchange (1 - phase) ** 3 for a more general PM expression where pmod could either be an Oscillator or Playbuf.

(
{
	var tFreq = 100;
	var trig = Impulse.ar(tFreq);
	var grainFreq = 400;

	var phase = Sweep.ar(trig, grainFreq);
	
	//var pmod = ???
	//var sig = sin(phase * (1 + (pmod * index)) * 2pi);
	var sig = sin((1 - phase) ** 3 * 2pi);

	var grainWindow = phase < 1;

	sig = sig * grainWindow;

	sig;

}.plot(0.02);
)

Does somebody know how this would look like for this specific case?

[QQQQ]

Is this what you were looking for? Phase modulation with a waveform read from a buffer.

What I have not been able to figure out so far is how this would work if the carrier was also a BufRd, rather than sin( (phase * 2pi)). I’d be grateful for suggestions.

b=Buffer.loadCollection(s, Signal.sineFill(2048, [1,00], 0!2))

(
{
	arg phase_buf = 0, form = 1, mod_depth = 1;



	var tFreq = 100;
	var trig = Impulse.ar(tFreq);

	var phase = Sweep.ar(trig, tFreq*form.max(1));

	var phase_mod = BufRd.ar(1, phase_buf, phase*BufFrames.kr(phase_buf), 1, 2);

	var sig = sin( (phase * 2pi) + (phase_mod * mod_depth).mod(2pi) );
	
	var grainWindow = phase < 1;

	sig = sig * grainWindow;

	sig

}.plot(0.02)
)

[dietcv]

thanks alot for your help

@QQQQ

how this would work if the carrier was also a BufRd

in this thread are some hints for such an implementation, which i cannot make any sense of in my case.
The Sweep.ar rate cant be multiplied by BufFrames.kr(b) * bufRateScale.ir(b) because its phase is also used for the grain window (this is fixed) and phi is not a BufRd but a SinOsc.
Here is my extraction of the pm example from the thread:

(
{
	var carr = 100;
	var mod = 200;
	var index = 2;

	var bufFrames = BufFrames.ir(b);
	var phase = Sweep.ar(0, carr * bufFrames * BufRateScale.ir(b));
	var phi = ((1 - SinOsc.ar(mod, pi/2)) * index).mod(2pi);

	var sig = BufRd.ar(1, b, (phase + (phi * bufFrames * BufRateScale.ir(b) / 2pi)).mod(bufFrames));

	sig;
	
}.plot(0.02)
)

however none of these examples does give me the desired end result. the phase modulator isnt a plain sine wave.

(
{	
	var tFreq = 100;
	var trig = Impulse.ar(tFreq);
	var grainFreq = 400;
	
	var phase = Sweep.ar(trig, grainFreq);
	
	var grainWindow = phase < 1;
	
	var sig = sin((1 - phase) ** 3 * 2pi);
	
	sig = sig * grainWindow;

	sig;
}.plot(0.005);
)

[QQQQ]

Thanks @dietcv for pointing me to that other thread and for suggesting a way to adapt it.

This is still a little messy, but it works:

b=Buffer.loadCollection(s, Signal.sineFill(2048, {rrand(0.0,1.0)}!3, 0!3))

(
{
	var carr = 100;
	var mod = 10;
	var index = 0.2;

	var bufFrames = BufFrames.kr(b);
	var phase = Sweep.ar(0, carr * bufFrames * BufRateScale.kr(b));

	var phi = (( 1 - BufRd.ar(1, b, (mod* phase + (0.25 * bufFrames * BufRateScale.kr(b))), 1, 2)) * index ).mod(2pi);

	var sig = BufRd.ar(1, b, (phase + (phi * bufFrames * BufRateScale.kr(b) / 2pi)).mod(bufFrames));

	sig;

}.plot(0.02)
)

Sorry this is still not the solution you are looking for!

[dietcv]

ok i think i got it!!!

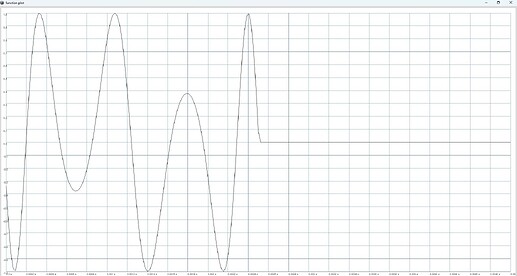
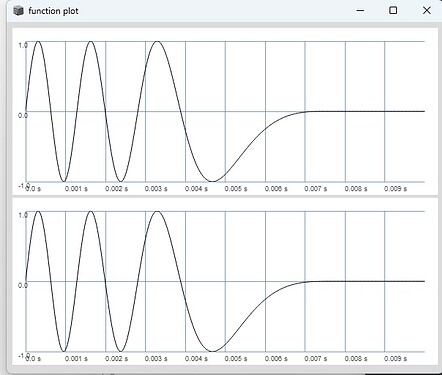
this is an ordinary PM implementation, just with an added window and a flipped phase for better comparision:

// ordinary PM

(
{
	var freq = 400;
	var mod = SinOsc.ar(freq * \mRatio.kr(1));
	var sig = SinOsc.ar(freq * \cRatio.kr(1), (mod * \index.kr(5)).wrap(0, 4pi));
	sig.neg * (Sweep.ar(0, freq) < 1);
}.plot(0.005);
)

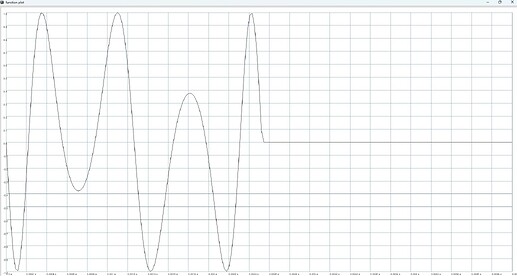
this BufRd pulsar implementation leads to the same result:

(
~freqBuf = Buffer.loadCollection(s, Signal.sineFill(2048, [1,0], 0!2));
~sndBuf = Buffer.loadCollection(s, Signal.sineFill(4096, [1,0], 0!2));
)

// pulsar BufRd PM with two sinusoids:

(
{
	var tFreq = \tFreq.kr(100);
	var trig = Impulse.ar(tFreq);
	var grainFreq = \freq.kr(400);
	var phase = Sweep.ar(trig, grainFreq);

	var phi = BufRd.ar(
		numChannels: 1,
		bufnum: ~freqBuf,
		phase: phase * BufFrames.kr(~freqBuf),
		loop: 0,
		interpolation: 4
	);

	var sig = BufRd.ar(
		numChannels: 1,
		bufnum: ~sndBuf,
		phase: 1 - (phase + ((phi * \index.kr(5)) / 2pi)) * BufFrames.kr(~sndBuf),
		loop: 1,
		interpolation: 4
	);

	sig * (phase < 1);

}.plot(0.005);
)

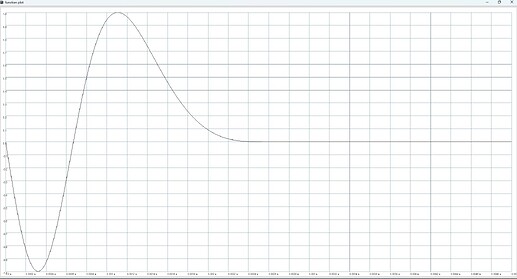
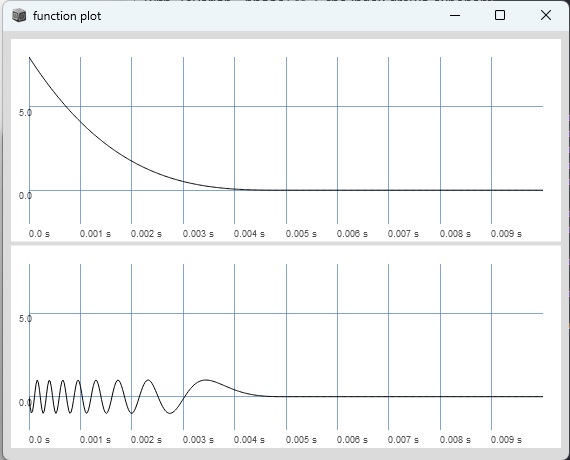
when instead using a welch window as the modulator and decreasing the modulation index from 5 to 2 you get the curved phase signal:

(
var welch = Env([0, 1, 0], [0.5, 0.5], \wel).discretize(4096);
~freqBuf = Buffer.sendCollection(s, welch, 1);
~sndBuf = Buffer.loadCollection(s, Signal.sineFill(4096, [1,0], 0!2));
)

// pulsar BufRd PM with welch window as a modulator

(
{
	var tFreq = \tFreq.kr(100);
	var trig = Impulse.ar(tFreq);
	var grainFreq = \freq.kr(400);
	var phase = Sweep.ar(trig, grainFreq);

	var phi = BufRd.ar(
		numChannels: 1,
		bufnum: ~freqBuf,
		phase: phase * BufFrames.kr(~freqBuf),
		loop: 0,
		interpolation: 4
	);

	var sig = BufRd.ar(
		numChannels: 1,
		bufnum: ~sndBuf,
		phase: 1 - (phase + ((phi * \index.kr(2)) / 2pi)) * BufFrames.kr(~sndBuf),
		loop: 1,
		interpolation: 4
	);

	sig * (phase < 1);

}.plot(0.005);
)

EDIT: i think the use of the welch window shows really nicely how frequency and phase are relatives of each other. Im wondering if i could use a ramp instead of a welch window when changing the interface.
thinking in terms of frequencies is a bit more straighforward then thinking of integrated frequency changes.
But i think the ordinary SinOsc as a modulator would not work anymore when changing the interface.

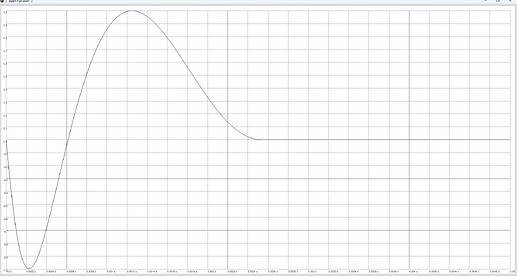
EDIT: using a curved ramp as the phase modulator and multiplying phi with the phase again does lead to something similiar, but then the SinOsc implementation doesnt work anymore, so ive introduced an index window:

(
var ramp = Env([1, 0], [1], [3.0]).discretize(4096);
~freqBuf = Buffer.sendCollection(s, ramp, 1);
~sndBuf = Buffer.loadCollection(s, Signal.sineFill(4096, [1,0], 0!2));
)

(
var statelessWindow = { |levels, times, curve, phase|
	var x = 0;
	var window = times.size.collect{ |i|
		var x2 = x + times[i];
		var result = (phase >= x) * (phase < x2) * phase.lincurve(x, x2, levels[i], levels[i+1], curve[i]);
		x = x2;
		result;
	}.sum;
	window * (phase < 1);
};

{
	var tFreq = \tFreq.kr(100);
	var trig = Impulse.ar(tFreq);
	var grainFreq = \freq.kr(400);
	var phase = Sweep.ar(trig, grainFreq);

	var phi = BufRd.ar(
		numChannels: 1,
		bufnum: ~freqBuf,
		phase: phase * BufFrames.kr(~freqBuf),
		loop: 0,
		interpolation: 4
	);

	var indexWindow = statelessWindow.(
		levels: [0, 1],
		times: [1],
		curve: [-8.0],
		phase: phase
	);
	var index = \index.kr(0) + indexWindow.linlin(0, 1, 0, \indexModAmount.kr(2));

	var sig = BufRd.ar(
		numChannels: 1,
		bufnum: ~sndBuf,
		phase: 1 - (phase + ((phi * index) / 2pi)) * BufFrames.kr(~sndBuf),
		loop: 1,
		interpolation: 4
	);

	sig * (phase < 1);

}.plot(0.005);
)

any suggestions?

[dietcv]

The welch window created by EnvGen is actually a half-sine window:

if you take the derivative of the half sine window which is a half cosine window and add ((grainFreq / overlap) * SampleDur.ir) to fmod, PM and FM are pretty much identical:

(
{
	var tFreq = 100;
	var trig = Impulse.ar(tFreq);
	var grainFreq = 400;
	var overlap = \overlap.kr(3).clip(0, grainFreq / tFreq);

	var phase = Sweep.ar(trig, grainFreq);
	var windowPhase = phase / overlap;
	var rectWindow = windowPhase < 1;

	var fmod = cos(windowPhase * pi) + ((grainFreq / overlap) * SampleDur.ir);
	var fm_phase = Sweep.ar(trig, grainFreq * (1 + (fmod * \index.kr(1))));

	var pmod = sin(windowPhase * pi);
	var pm_phase = phase + ((pmod * overlap) / pi);

	var pm_sig = sin(pm_phase * 2pi);
	var fm_sig = sin(fm_phase * 2pi);

	[pm_sig * rectWindow, fm_sig * rectWindow];

}.plot(0.01);
)

(1 - phase) ** 3 is quite similiar for overlap == 1. If you increase overlap and exchange (1 - phase) ** 3 with (overlap - phase) ** 3 the index grows exponentially if you change overlap, with the half cosine window for FM or the half sine window for PM the index grows linearly when you change overlap.

(
{
	var tFreq = 100;
	var trig = Impulse.ar(tFreq);
	var grainFreq = 400;
	var phase = Sweep.ar(trig, grainFreq);
	var overlap = \overlap.kr(2).clip(0, grainFreq / tFreq);

	var windowPhase = phase / overlap;
	var rectWindow = windowPhase < 1;

	var pulsaretPhase = (overlap - phase) ** 3;
	
	var sig = sin(pulsaretPhase * 2pi);
	
	[pulsaretPhase * rectWindow, sig * rectWindow];

}.plot(0.01);
)