Frequency instead of phase

Questions
31

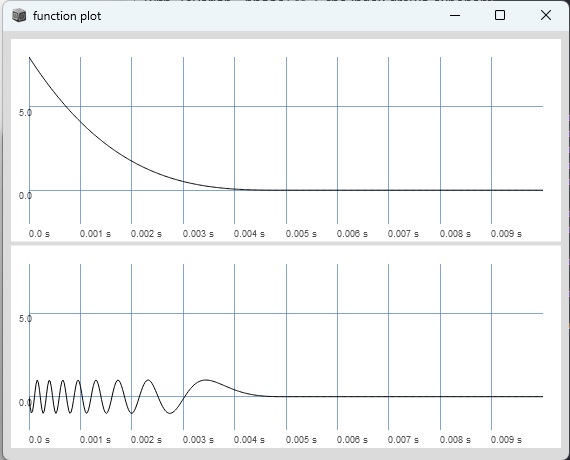
The welch window created by EnvGen is actually a half-sine window:

if you take the derivative of the half sine window which is a half cosine window and add ((grainFreq / overlap) * SampleDur.ir) to fmod, PM and FM are pretty much identical:

(
{
	var tFreq = 100;
	var trig = Impulse.ar(tFreq);
	var grainFreq = 400;
	var overlap = \overlap.kr(3).clip(0, grainFreq / tFreq);

	var phase = Sweep.ar(trig, grainFreq);
	var windowPhase = phase / overlap;
	var rectWindow = windowPhase < 1;

	var fmod = cos(windowPhase * pi) + ((grainFreq / overlap) * SampleDur.ir);
	var fm_phase = Sweep.ar(trig, grainFreq * (1 + (fmod * \index.kr(1))));

	var pmod = sin(windowPhase * pi);
	var pm_phase = phase + ((pmod * overlap) / pi);

	var pm_sig = sin(pm_phase * 2pi);
	var fm_sig = sin(fm_phase * 2pi);

	[pm_sig * rectWindow, fm_sig * rectWindow];

}.plot(0.01);
)

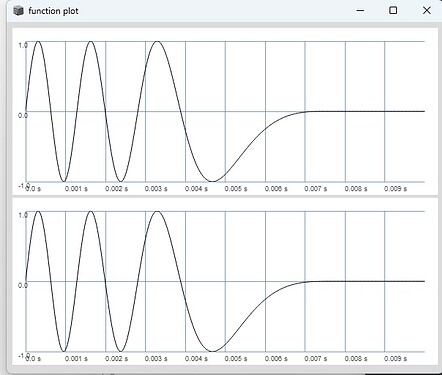
asdasdad
asdasdad605×512 48.4 KB

(1 - phase) ** 3 is quite similiar for overlap == 1. If you increase overlap and exchange (1 - phase) ** 3 with (overlap - phase) ** 3 the index grows exponentially if you change overlap, with the half cosine window for FM or the half sine window for PM the index grows linearly when you change overlap.

(
{
	var tFreq = 100;
	var trig = Impulse.ar(tFreq);
	var grainFreq = 400;
	var phase = Sweep.ar(trig, grainFreq);
	var overlap = \overlap.kr(2).clip(0, grainFreq / tFreq);

	var windowPhase = phase / overlap;
	var rectWindow = windowPhase < 1;

	var pulsaretPhase = (overlap - phase) ** 3;
	
	var sig = sin(pulsaretPhase * 2pi);
	
	[pulsaretPhase * rectWindow, sig * rectWindow];

}.plot(0.01);
)

rgaighi