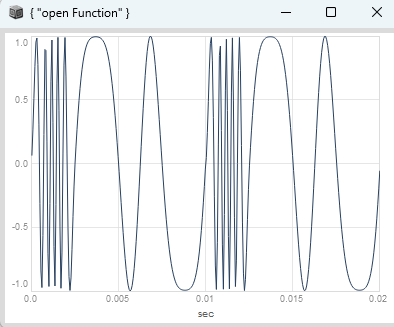
one additional thing:
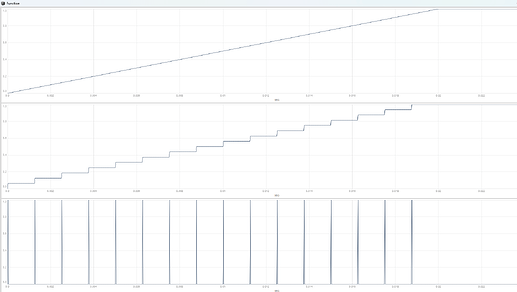
from your plot i have noticed, that you probably want to have a pulsaret train (several single carrier cycles) with a grain frequency trajectory.
In pulsar synthesis the grain duration is determined by the grain frequency, higher grain frequencies mean shorter grain durations and vice versa. In other types of microsound the grain duration is dependent on the trigger frequency instead. So for having this grain frequency trajectory per pulsaret train you cant use FM, because the grain durations would get shortened, if the grain frequency gets higher while beeing modulated.
Instead you could use Phase Modulation or Phase Distortion, which is when beeing implemented as “phase increment distortion” a subset of PM.
There are two types of phase distortion, the first is called “phase shaping”. Its similar to “wave shaping” where you take a signal and put it through a non-linear transfer function, but applied to the phase of a signal.
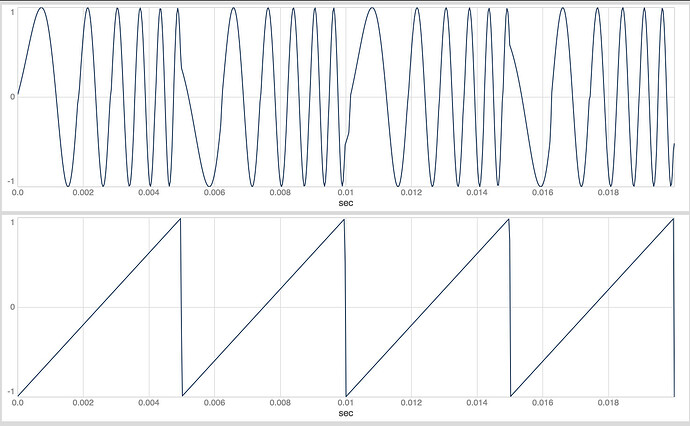
classic PD as “phase shaping”
(
var transferFunc = { |phase, skew|
phase = phase.linlin(0, 1, skew.neg, 1 - skew);
phase.bilin(0, skew.neg, 1 - skew, 0.5, 0, 1);
};
{
var skew = \skew.kr(0.125);
var phase = Phasor.ar(0, 100 * SampleDur.ir);
cos(transferFunc.(phase, skew) * 2pi).neg;
}.plot(0.02);
)
With “phase increment distortion” you have a classic PM formula → phase + (mod * index), but add a non-linear unipolar modulation signal, like a window function (lets call this a frequency window even when beeing applied to the phase) to your linear phase.
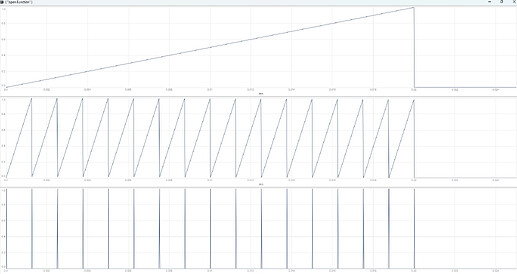
classic PD as “phase increment distortion”
(
var transferFunc = { |phase, skew|
phase = phase.linlin(0, 1, skew.neg, 1 - skew);
phase.bilin(0, skew.neg, 1 - skew, 1, 0, 0);
};
{
var skew = \skew.kr(0.125);
var phase = Phasor.ar(0, 100 * SampleDur.ir);
cos(phase + (transferFunc.(phase, skew) * (0.5 - skew)) * 2pi).neg;
}.plot(0.02);
)
The beauty of the “phase increment distortion” method in our context is, that you dont have to use the same phase to drive your carrier and your modulator. This is perfect for pulsar synthesis. Because you want to use the grainPhase to drive your carrier and the windowPhase to drive the modulator.
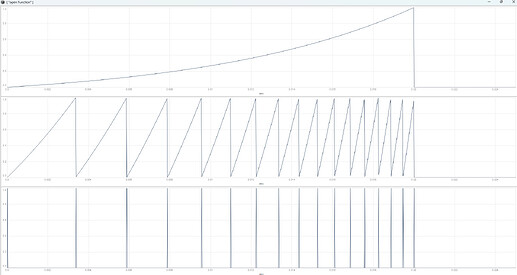
Here with a simple half sine cycle as a modulator. Use a different sign to change direction of the sweep and adjust the duty cycle with overlap to your liking. Also try out different modulation functions.
(
{
var tFreq = 100;
var trig = Impulse.ar(tFreq);
var grainFreq = 800;
var overlap = min(\overlap.kr(5), grainFreq / tFreq);
var phase = Sweep.ar(trig, grainFreq);
var windowPhase = phase / overlap;
var rectWindow = windowPhase < 1;
var mod = sin(windowPhase * pi);
var sig = sin(phase + (mod * \index.kr(-1) * overlap / pi) * 2pi);
sig * rectWindow;
}.plot(0.02);
)
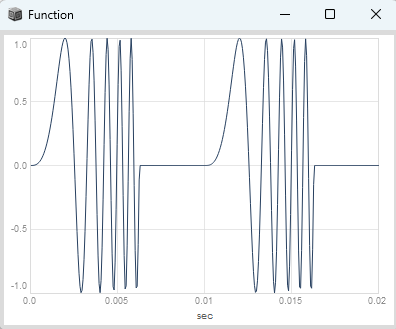
combine “phase shaping” and “phase increment distortion” for a more complex modulator, here the modulator has a skew param:
(
var transferFunc = { |phase, skew|
phase = phase.linlin(0, 1, skew.neg, 1 - skew);
phase.bilin(0, skew.neg, 1 - skew, 0.5, 0, 1);
};
{
var tFreq = 100;
var trig = Impulse.ar(tFreq);
var grainFreq = 400;
var overlap = min(\overlap.kr(4), grainFreq / tFreq);
var phase = Sweep.ar(trig, grainFreq);
var windowPhase = phase / overlap;
var rectWindow = windowPhase < 1;
var skew = \skew.kr(0.25);
var mod = cos(transferFunc.(windowPhase, skew) * 2pi).neg * 0.5 + 0.5;
var sig = sin(phase + (mod * (0.5 - skew) * \index.kr(4) * overlap) * 2pi);
sig * rectWindow;
}.plot(0.02);
)