hey,
i have succesfully built the ramp2slope and ramp2trig abstractions from the ~gen book with some help from @Sam_Pluta:
var rampToSlope = { |phase|
var history = Delay1.ar(phase);
var delta = (phase - history);
delta.wrap(-0.5, 0.5);
};
var rampToTrig = { |phase|
var history = Delay1.ar(phase);
var delta = (phase - history);
var sum = (phase + history);
var trig = (delta / sum).abs > 0.5;
Trig1.ar(trig, SampleDur.ir);
};
TL:TR How do i count the number of samples correctly in the following example:
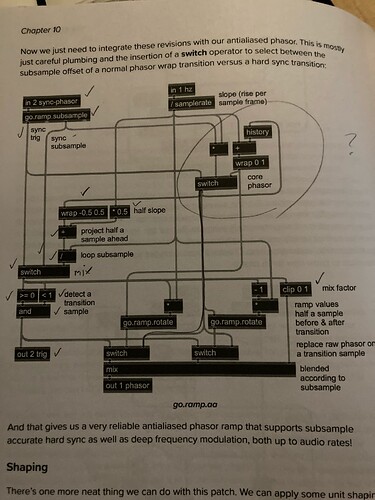
In the gen~ book is a chapter about creating sub-sample accurate events from phasor ramps (i wont get into the details here why getting triggers from ramps could be better then creating ramps froms triggers). It is stated that:
The polyphonic patches we have created so far trigger grains with sample-accurate timing, in the sense that the trigger aligns each grain to the precise sample frame during which the phasor ramp wraps. This is already much more precise than typical control rates. But the smaller the grains get, and the faster they are spawned, the more the sound can transform into a pitched oscillator. At these rates, the fractional subsample locations of events become very important, and we need to locate each event precisely within a sample frame with sub-sample accurancy
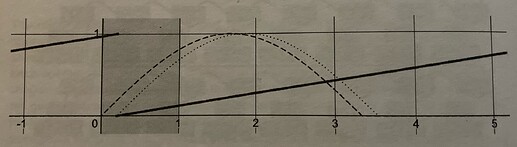
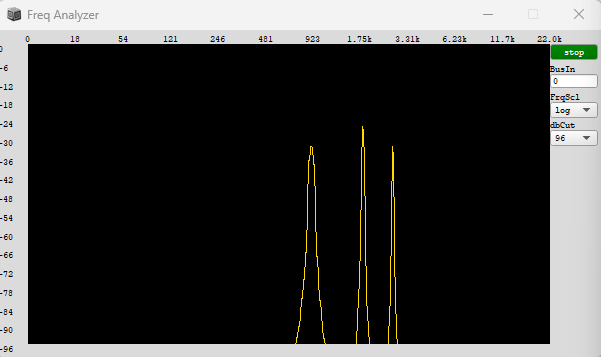
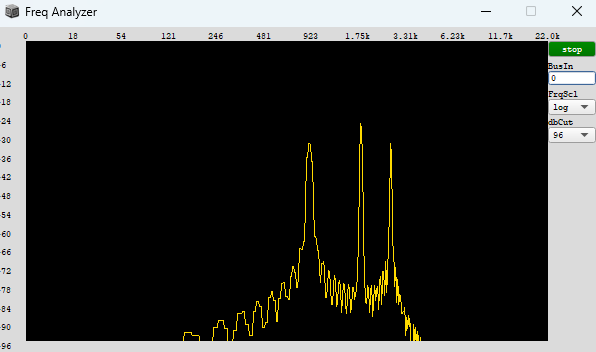
Lets zoom right in to where the scheduler phasor wraps and take a look at the grain envelope it causes.
In this graph, the horizontal axis represents the passing sample frames in real-time, and the solid line the continuous high-frequency ramp that our phasor creates.
The gray shaded region is a specific sample frame in which the phasor has wrapped, causing a trigger, and the dashed line shows a grain envelope caused by this trigger. But for a pure tone, the grain window should be aligned to the ideal ramp, as marked by the dotted line:
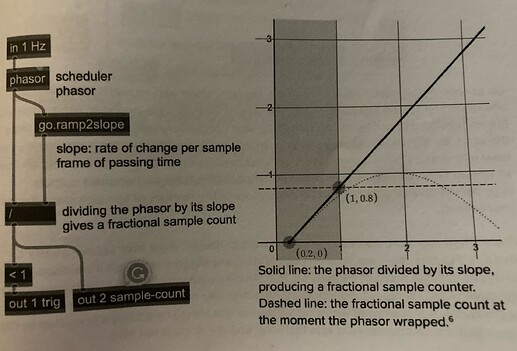
The book suggests calculating the subsample offset of the ramp during the trigger to properly align the grain window.
To calculate the subsample offset you can divide the phasor by its own slope, to get a ramp with a slope of 1.0. Such a slope counts by one for each passing sample frame of time. Then, in the exact sample frame that the phasor wraps, the first value will always be some number between zero and one, giving us the fractional number of samples since it wrapped:
in SC code this would look like this:
(
var rampToSlope = { |phase|
var history = Delay1.ar(phase);
var delta = (phase - history);
delta.wrap(-0.5, 0.5);
};
{
var rate = 1000;
var phase = (Phasor.ar(0, rate * SampleDur.ir) - SampleDur.ir).wrap(0, 1);
var slope = rampToSlope.(phase);
var sampleCount = phase / slope;
var trig = sampleCount < 1;
[phase, trig];
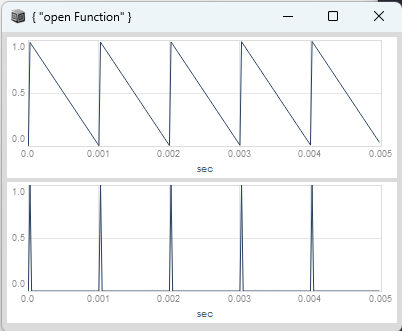
}.plot(0.005);
)
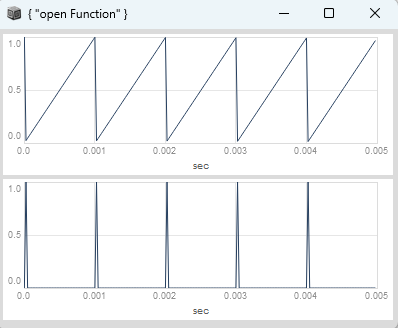
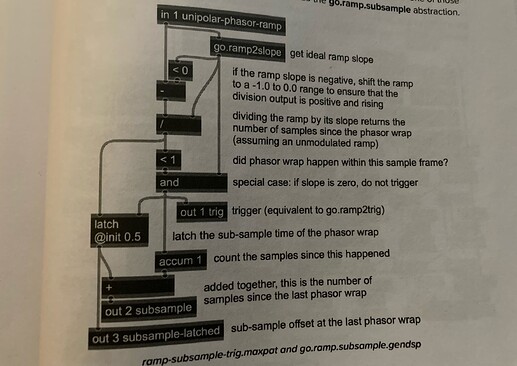
There are a few subtleties to deal with, though. First, we have to ensure we are getting a steady rate of change of the ramp even through the transition, which we handled using the ramp2slope abstraction.
Unfortunately this patch doesnt work for a phasor running downwards, as it will focus on the values near the top of the ramp rather then near zero. We can fix that simply by subtracting one from the phasor to recenter it, but only if the slope is negative:
in SC code this would look like this:
(
var rampToSlope = { |phase|
var history = Delay1.ar(phase);
var delta = (phase - history);
delta.wrap(-0.5, 0.5);
};
{
var rate = 1000;
// handles downward ramps
var phase = (Phasor.ar(0, rate * SampleDur.ir) - SampleDur.ir).wrap(0, 1).linlin(0, 1, 1, 0);
var slope = rampToSlope.(phase);
var sampleCount = phase - (slope < 0) / slope;
var trig = sampleCount < 1;
[phase, trig];
}.plot(0.005);
)
Up to now, this algorithm assumes that the phasors slope isnt changing. That actually doesnt matter for the first sample after the phasor wrap, but beyond that, simply dividing the accumulated phase by the current slope wont accurately tell you the samples since the wrap. We can fix this easily enough by grabbing the fractional count at the wrap as we have above and storing it with a latch operator, and also restarting a sample counter using an accum operator at the same time. Adding both the latch and accum outputs together will give an accurate fractional measure of the number of samples since the last phasor wrap.
There is also a second condition added which handles triggers when the phasors frequency is set to zero. But i think i wont need that, so we can skip that second condition (would also not know how to implement the conditial and):
My attempt to translate this code has been the following, but im not sure about the counter / accumulator:
(
var rampToSlope = { |phase|
var history = Delay1.ar(phase);
var delta = (phase - history);
delta.wrap(-0.5, 0.5);
};
{
var rate = 1000;
var phase = (Phasor.ar(0, rate * SampleDur.ir) - SampleDur.ir).wrap(0, 1);
var slope = rampToSlope.(phase);
var sampleCount = phase - (slope < 0) / slope;
var trig = sampleCount < 1;
var latch = Latch.ar(sampleCount, trig);
// TODO: count the number of samples correctly
var accum = Demand.ar(trig, 0, Dseries(0, 1, inf)) * SampleDur.ir;
var subsample = latch + accum;
[phase, trig];
}.plot(0.005);
)
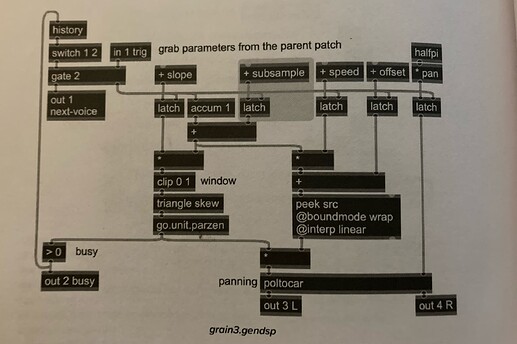
This sub-sample accurate triggers should then be used to trigger a grain window. As far as i understand it, the phase which drives the grain window is calculated by using the sum of the latched subsample offset and a trigger accumulator multiplied by the slope.
How do i count the number of samples correctly? thanks